Đề Thi Thử Tốt Nghiệp 2022 Môn Lý Online Bám Sát Đề Tham Khảo (Đề 1)
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-2022-mon-ly-online-bam-sat-de-tham-khao-de-1
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp 2022 Môn Lý Online Bám Sát Đề Tham Khảo (Đề 1)
không đổi nhưng hướng thay đổi.
Đường elip.
biên độ và tốc độ.
\(\frac{1}{{2\pi f}}\).
0,25 s.
2,25 N.
luôn nằm ngang và vuông góc với phương truyền sóng.
28 Hz.
Sóng âm chỉ truyền được trong không khí.
vận tốc âm.
5.
141 V.
R, L và C
phần tạo ra dòng điện là phần ứng.
cuộn sơ cấp là cuộn nối với nguồn điện cần biến đổi hiệu điện thế.
220\(\sqrt 2 \)V.
\(e = 2\sin \left( {100\pi t + \frac{\pi }{4}} \right)(V).\)
2,5 kV.
Sóng điện từ lan truyền được trong chân không.
\(C = \frac{1}{{2\pi }}pF.\)
các vệt sáng tối xen kẽ nhau.
\(\lambda \)
\(k\frac{\lambda }{2}\)
Tia Rơnghen.
9,9 mm
tăng diện tích kim loại được chiếu sáng.
Độ định hướng cao.
\({\lambda _1},{\lambda _2}\) và \({\lambda _3}\)
cùng số proton nhưng khác nhau số notron.
\({{\text{W}}_{lkr}} = \frac{1}{Z}\left[ {Z{m_p} + (A - Z){m_n} - {m_X}} \right].{c^2}\)
5 proton và 6 notron.
nước nguyên chất.
các electron.
không đổi.
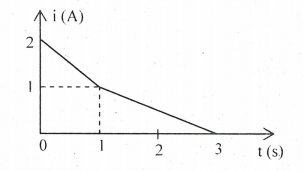 Gọi suất điện động tự cảm trong mạch trong khoảng thời gian từ 0 đến 1s là e1, từ 1s đến 3s là e2. Ta có:
Gọi suất điện động tự cảm trong mạch trong khoảng thời gian từ 0 đến 1s là e1, từ 1s đến 3s là e2. Ta có:\({e_1} = 0,5{e_2}\)
\(10\sqrt 2 ra{\text{d}}/s\)
20,0 MeV
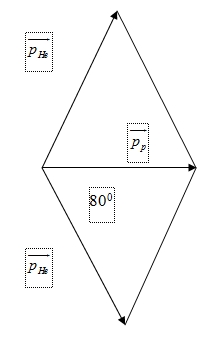 Áp dụng định lý sin trong tam giác ta có:\(\frac{{{p_{He}}}}{{\sin {{80}^0}}} = \frac{{{p_p}}}{{\sin {{20}^0}}} \Leftrightarrow \frac{{{p^2}_{He}}}{{{{\sin }^2}{{80}^0}}} = \frac{{{p^2}_p}}{{{{\sin }^2}{{20}^0}}} \Leftrightarrow \frac{{2.{m_{He}}.{K_{He}}}}{{{{\sin }^2}{{80}^0}}} = \frac{{2{m_p}.{K_p}}}{{{{\sin }^2}{{20}^0}}}\)\({K_p} = \frac{1}{2}.{m_p}.v_p^2 = \frac{1}{2}.1,0072u.0,1{c^2}.931,5MeV/{c^2} = 4,69MeV\)\( = > {K_{He}} = \frac{{2{m_p}.{K_p}}}{{{{\sin }^2}{{20}^0}}}.\frac{{{{\sin }^2}{{80}^0}}}{{2.{m_{He}}}} = 9,72MeV\)Năng lượng của phản ứng là: \(\Delta E = {K_{He}} – {K_p} = 2.9,72 – 4,69 = 14,75MeV\)
Áp dụng định lý sin trong tam giác ta có:\(\frac{{{p_{He}}}}{{\sin {{80}^0}}} = \frac{{{p_p}}}{{\sin {{20}^0}}} \Leftrightarrow \frac{{{p^2}_{He}}}{{{{\sin }^2}{{80}^0}}} = \frac{{{p^2}_p}}{{{{\sin }^2}{{20}^0}}} \Leftrightarrow \frac{{2.{m_{He}}.{K_{He}}}}{{{{\sin }^2}{{80}^0}}} = \frac{{2{m_p}.{K_p}}}{{{{\sin }^2}{{20}^0}}}\)\({K_p} = \frac{1}{2}.{m_p}.v_p^2 = \frac{1}{2}.1,0072u.0,1{c^2}.931,5MeV/{c^2} = 4,69MeV\)\( = > {K_{He}} = \frac{{2{m_p}.{K_p}}}{{{{\sin }^2}{{20}^0}}}.\frac{{{{\sin }^2}{{80}^0}}}{{2.{m_{He}}}} = 9,72MeV\)Năng lượng của phản ứng là: \(\Delta E = {K_{He}} – {K_p} = 2.9,72 – 4,69 = 14,75MeV\)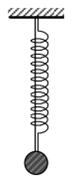 Lò xo có độ cứng k1 = 10 N/m, sợi dây khi bị kéo dãn xuất hiện lực đàn hồi có độ lớn tỷ lệ với độ giãn của sợi dây với hệ số đàn hồi k2 = 30 N/m ( sợi dây khi bị kéo dãn tương đương như một lò xo, khi dây bị cùng luwjcj đàn hồi triệt tiêu ) Ban đầu vật đang ở vị trí cân bằng, kéo vật thẳng đứng xuống dưới một đoạn a = 5 cm rồi thả nhẹ. Khoảng thời gian kể từ khi thả cho đến khi vật đạt độ cao cực đại lần thứ nhất xấp xỉ bằng
Lò xo có độ cứng k1 = 10 N/m, sợi dây khi bị kéo dãn xuất hiện lực đàn hồi có độ lớn tỷ lệ với độ giãn của sợi dây với hệ số đàn hồi k2 = 30 N/m ( sợi dây khi bị kéo dãn tương đương như một lò xo, khi dây bị cùng luwjcj đàn hồi triệt tiêu ) Ban đầu vật đang ở vị trí cân bằng, kéo vật thẳng đứng xuống dưới một đoạn a = 5 cm rồi thả nhẹ. Khoảng thời gian kể từ khi thả cho đến khi vật đạt độ cao cực đại lần thứ nhất xấp xỉ bằng0,751 s.
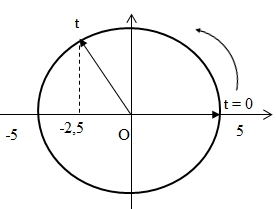 => Góc quét: \({\alpha _1} = \frac{\pi }{2} + \frac{\pi }{6} = \frac{{2\pi }}{3} \Rightarrow {t_1} = \frac{{2\pi }}{3}\frac{T}{{2\pi }} = \frac{{2\pi }}{3}.\frac{{0,1\pi }}{{2\pi }} = \frac{\pi }{{30}}s\)Tại li độ x = -2,5cm vật có vận tốc: \(v = \omega \sqrt {{A^2} – {x^2}} = \frac{{2\pi }}{{0,1\pi }}\sqrt {{5^2} – 2,{5^2}} = 50\sqrt 3 \left( {cm/s} \right)\)- Giai đoạn 2:Độ giãn của lò xo ở VTCB: \(\Delta l' = \frac{{mg}}{{{k_1}}} = 10cm\) => tại vị trí lò xo không biến dạng x = -10cmVật dao động điều hoà với chu kì và biên độ: \(\left\{ \begin{gathered} T' = 2\pi \sqrt {\frac{m}{{{k_1}}}} = 2\pi \sqrt {\frac{{0,1}}{{10}}} = 0,2\pi \left( s \right) \Rightarrow \omega ' = \frac{{2\pi }}{{0,2\pi }} = 10rad/s \hfill \\ A' = \sqrt {{x^2} + \frac{{{v^2}}}{{{{\omega '}^2}}}} = \sqrt {{{\left( { – 10} \right)}^2} + \frac{{{{\left( {50\sqrt 3 } \right)}^2}}}{{{{10}^2}}}} = 5\sqrt 7 cm \hfill \\ \end{gathered} \right.\)Vật đi từ vị trí x = -∆l = -10cm đến biên âm \(x = – 5\sqrt 7 cm\) được biểu diễn trên đường tròn lượng giác:
=> Góc quét: \({\alpha _1} = \frac{\pi }{2} + \frac{\pi }{6} = \frac{{2\pi }}{3} \Rightarrow {t_1} = \frac{{2\pi }}{3}\frac{T}{{2\pi }} = \frac{{2\pi }}{3}.\frac{{0,1\pi }}{{2\pi }} = \frac{\pi }{{30}}s\)Tại li độ x = -2,5cm vật có vận tốc: \(v = \omega \sqrt {{A^2} – {x^2}} = \frac{{2\pi }}{{0,1\pi }}\sqrt {{5^2} – 2,{5^2}} = 50\sqrt 3 \left( {cm/s} \right)\)- Giai đoạn 2:Độ giãn của lò xo ở VTCB: \(\Delta l' = \frac{{mg}}{{{k_1}}} = 10cm\) => tại vị trí lò xo không biến dạng x = -10cmVật dao động điều hoà với chu kì và biên độ: \(\left\{ \begin{gathered} T' = 2\pi \sqrt {\frac{m}{{{k_1}}}} = 2\pi \sqrt {\frac{{0,1}}{{10}}} = 0,2\pi \left( s \right) \Rightarrow \omega ' = \frac{{2\pi }}{{0,2\pi }} = 10rad/s \hfill \\ A' = \sqrt {{x^2} + \frac{{{v^2}}}{{{{\omega '}^2}}}} = \sqrt {{{\left( { – 10} \right)}^2} + \frac{{{{\left( {50\sqrt 3 } \right)}^2}}}{{{{10}^2}}}} = 5\sqrt 7 cm \hfill \\ \end{gathered} \right.\)Vật đi từ vị trí x = -∆l = -10cm đến biên âm \(x = – 5\sqrt 7 cm\) được biểu diễn trên đường tròn lượng giác: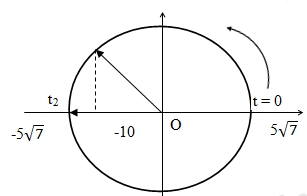 Từ đường tròn lượng giác ta tính được: \({\alpha _2} = 0,71rad \Rightarrow {t_2} = \frac{{{\alpha _2}}}{{\omega '}} = 0,071s\) => Khoảng thời gian kể từ khi thả vật đến khi vật đạt độ cao cực đại: t = t1 + t2 = 0,175s
Từ đường tròn lượng giác ta tính được: \({\alpha _2} = 0,71rad \Rightarrow {t_2} = \frac{{{\alpha _2}}}{{\omega '}} = 0,071s\) => Khoảng thời gian kể từ khi thả vật đến khi vật đạt độ cao cực đại: t = t1 + t2 = 0,175s46,0 dB
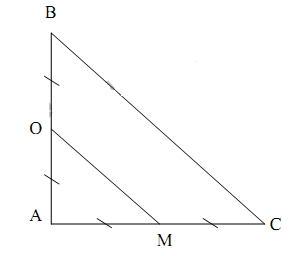 Khi nguồn âm O đặt tại B, người đứng tại C nghe được âm có mức cường độ âm: \({L_C} = 10.\log \frac{P}{{4\pi .B{C^2}}} = 40dB\)Khi di chuyển nguồn O trên đoạn AB và người M di chuyển trên đoạn AC sao cho BO = AM thì mức cường độ âm người nghe được: \({L_M} = 10.\log \frac{P}{{4\pi .O{M^2}}}\)Ta có: \({\left( {{L_M}} \right)_{\max }} \Leftrightarrow O{M_{\min }}\)∆ABC vuông cân tại A có BO = AM => OMmin <=> OM là đường trung bình của ∆ABC\( \Rightarrow O{M_{\min }} = \frac{{BC}}{2} \Rightarrow {\left( {{L_M}} \right)_{m{\text{ax}}}} = 10.\log \frac{P}{{4\pi .{{\left( {\frac{{BC}}{2}} \right)}^2}}} = 10.\log \frac{{4P}}{{4\pi .B{C^2}}}\)\( \Rightarrow {\left( {{L_M}} \right)_{\max }} – {L_C} = 10.\log \frac{{4P}}{{4\pi .B{C^2}}} – 10.\log \frac{P}{{4\pi .B{C^2}}} = 10\log 4 \Rightarrow {\left( {{L_M}} \right)_{\max }} = {L_C} + 10\log 4\)\( \Rightarrow {\left( {{L_M}} \right)_{\max }} = 40 + 10\log 4 = 46dB\)
Khi nguồn âm O đặt tại B, người đứng tại C nghe được âm có mức cường độ âm: \({L_C} = 10.\log \frac{P}{{4\pi .B{C^2}}} = 40dB\)Khi di chuyển nguồn O trên đoạn AB và người M di chuyển trên đoạn AC sao cho BO = AM thì mức cường độ âm người nghe được: \({L_M} = 10.\log \frac{P}{{4\pi .O{M^2}}}\)Ta có: \({\left( {{L_M}} \right)_{\max }} \Leftrightarrow O{M_{\min }}\)∆ABC vuông cân tại A có BO = AM => OMmin <=> OM là đường trung bình của ∆ABC\( \Rightarrow O{M_{\min }} = \frac{{BC}}{2} \Rightarrow {\left( {{L_M}} \right)_{m{\text{ax}}}} = 10.\log \frac{P}{{4\pi .{{\left( {\frac{{BC}}{2}} \right)}^2}}} = 10.\log \frac{{4P}}{{4\pi .B{C^2}}}\)\( \Rightarrow {\left( {{L_M}} \right)_{\max }} – {L_C} = 10.\log \frac{{4P}}{{4\pi .B{C^2}}} – 10.\log \frac{P}{{4\pi .B{C^2}}} = 10\log 4 \Rightarrow {\left( {{L_M}} \right)_{\max }} = {L_C} + 10\log 4\)\( \Rightarrow {\left( {{L_M}} \right)_{\max }} = 40 + 10\log 4 = 46dB\)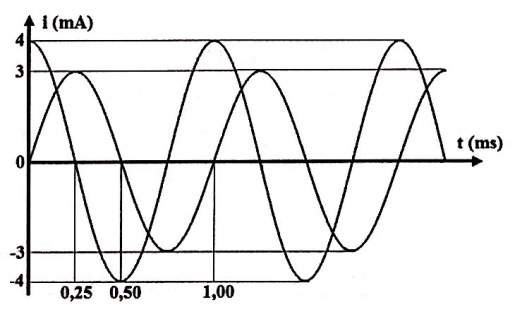 Tổng điện tích của hai tụ điện trong hai mạch ở cùng một thời điểm có giá trị lớn nhất bằng
Tổng điện tích của hai tụ điện trong hai mạch ở cùng một thời điểm có giá trị lớn nhất bằng5/π (µC).
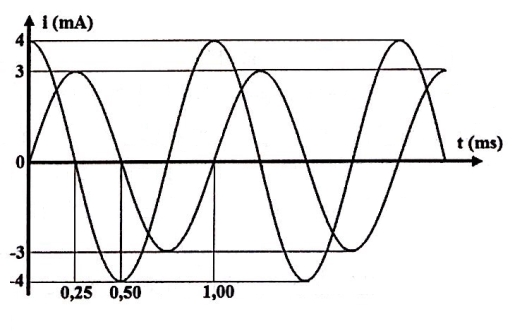 Biểu thức các dòng điện: \({i_1} = 4\cos 2000\pi t\left( {mA} \right),\,{i_2} = 3\cos \left( {2000\pi t – 0,5\pi } \right)\left( {mA} \right).\) \( \Rightarrow i = {i_1} + {i_2} = 4 + 3\angle \left( { – 0,5\pi } \right) = 5\angle \left( { – 0,6435} \right) \Rightarrow {I_0} = 5\left( {mA} \right)\) \( \Rightarrow {Q_0} = \frac{{{I_0}}}{\omega } = \frac{{2,5}}{\pi }{.10^{ – 6}}\left( C \right) \Rightarrow \) .
Biểu thức các dòng điện: \({i_1} = 4\cos 2000\pi t\left( {mA} \right),\,{i_2} = 3\cos \left( {2000\pi t – 0,5\pi } \right)\left( {mA} \right).\) \( \Rightarrow i = {i_1} + {i_2} = 4 + 3\angle \left( { – 0,5\pi } \right) = 5\angle \left( { – 0,6435} \right) \Rightarrow {I_0} = 5\left( {mA} \right)\) \( \Rightarrow {Q_0} = \frac{{{I_0}}}{\omega } = \frac{{2,5}}{\pi }{.10^{ – 6}}\left( C \right) \Rightarrow \) .