Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Lý Online-Đề 4
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-thpt-nam-2023-mon-ly-online-de-4
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Lý Online-Đề 4
tần số âm.
V.m2.
\(i = \frac{{\lambda a}}{{2D}}\).
\({Z_{\text{L}}} = 3{Z_{\text{C}}}\).
\(mg\ell \left( {\cos \alpha - \cos {\alpha _0}} \right)\)
\(2n\pi \) với \(n = 0, \pm 1, \pm 2, \ldots \)
Tia hồng ngoại.
v = 12 m/s.
14 .
\(U = \frac{{{U_0}}}{2}\).
Tia laze dùng truyền thông thông tin bằng cáp quang.
tăng giá trị hiệu dụng của điện áp xoay chiều.
Hiện tượng điện phân.
giảm liên tục theo thời gian.
Mạch biến điệu.
\({v^2} = \frac{k}{m}({A^2} - {x^2})\).
1,77 eV
\({W_{{\text{lk}}}} = \left[ {Z{m_{\text{p}}} + \left( {A - Z} \right){m_{\text{n}}} + {m_{\text{X}}}} \right]{c^2}\)
\({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda \) với \(k = 0, \pm 1, \pm 2, \ldots \)
Ánh sáng Mặt Trời không phải là ánh sáng đơn sắc.
\({\text{cos}}\varphi = \frac{R}{Z}\).
\(q.E/d\).
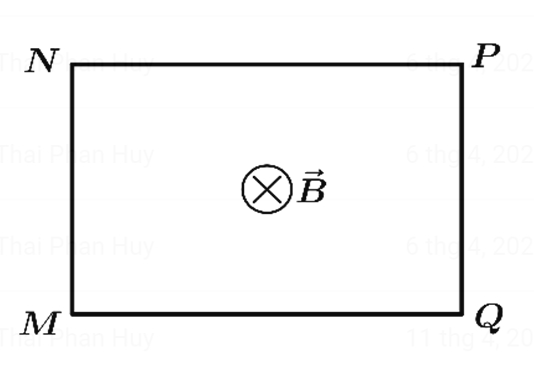 Trong khung dây có dòng điện chạy theo chiều \(MNPQM\). Lực từ tác dụng lên cạnh \(PQ\) cùng hướng với
Trong khung dây có dòng điện chạy theo chiều \(MNPQM\). Lực từ tác dụng lên cạnh \(PQ\) cùng hướng vớivecto \(\overrightarrow {PQ} \).
0,25 J.
\(0,50 mm\).
3,1.1011J.
0,50 .
\(78,{5.10^{ - 3}}A\).
\(2,{2.10^3}\).
\(7 B\).
\(385 nm\).
 Độ lệch pha của điện áp hai đầu đoạn mạch với cường độ dòng điện trong mạch là
Độ lệch pha của điện áp hai đầu đoạn mạch với cường độ dòng điện trong mạch là\(0,524{\text{rad}}\).
\({\text{180 V}}\).
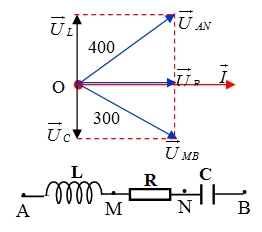 Cách 1: Cách đại số (truyền thống).*\(\left\{ {\begin{array}{*{20}{c}} {U_{RL}^2 = U_R^2 + U_L^2} \\ {U_{RC}^2 = U_R^2 + U_C^2} \end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{{400}^2} = U_R^2 + U_L^2} \\ {{{300}^2} = U_R^2 + U_C^2} \end{array} \Rightarrow {{\left( {{U_L}{U_C}} \right)}^2} = \left( {{{400}^2} – U_R^2} \right)\left( {{{300}^2} – U_R^2} \right)} \right.} \right..\) *\({\overrightarrow U _{RL}} \bot {\overrightarrow U _{RC}} \Rightarrow \tan {\varphi _{RL}}.\tan {\varphi _{RC}} = – 1 = \frac{{{U_L}}}{{{U_R}}}.\frac{{ – {U_C}}}{{{U_R}}} = – 1 \Rightarrow {U_L}{U_C} = U_R^2.\) Do đó: \({\left( {{U_L}{U_C}} \right)^2} = \left( {{{300}^2} – U_R^2} \right)\left( {{{400}^2} – U_R^2} \right) = U_R^4 \Rightarrow {U_R} = 240\left( {\text{V}} \right).\) Bình luận: Cách giải này khó ở chỗ là giải phương trình bậc 4 của R.Cách 2: Dùng phương pháp giản đồ vectơ buộc*Bài toán liên quan đến điện áp bắt chéo nên ta tổng hợp theo quy tắc hình bình hành các vecto điện áp \(\left\{ {\begin{array}{*{20}{c}} {{{\overrightarrow U }_{AN}} = {{\overrightarrow U }_R} + {{\overrightarrow U }_L}} \\ {{{\overrightarrow U }_{MB}} = {{\overrightarrow U }_R} + {{\overrightarrow U }_C}} \end{array}} \right..\) Do \({\overrightarrow U _{AN}} \bot {\overrightarrow U _{NB}},\) nên \(\Delta O{U_{AN}}{U_{MB}}\) vuông.Suy ra \(\frac{1}{{U_R^2}} = \frac{1}{{U_{AN}^2}} + \frac{1}{{U_{MB}^2}}.\) Hay \(\frac{1}{{U_R^2}} = \frac{1}{{{{300}^2}}} + \frac{1}{{{{400}^2}}} \Leftrightarrow {U_R} = 240\left( {\text{V}} \right).\)
Cách 1: Cách đại số (truyền thống).*\(\left\{ {\begin{array}{*{20}{c}} {U_{RL}^2 = U_R^2 + U_L^2} \\ {U_{RC}^2 = U_R^2 + U_C^2} \end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{{400}^2} = U_R^2 + U_L^2} \\ {{{300}^2} = U_R^2 + U_C^2} \end{array} \Rightarrow {{\left( {{U_L}{U_C}} \right)}^2} = \left( {{{400}^2} – U_R^2} \right)\left( {{{300}^2} – U_R^2} \right)} \right.} \right..\) *\({\overrightarrow U _{RL}} \bot {\overrightarrow U _{RC}} \Rightarrow \tan {\varphi _{RL}}.\tan {\varphi _{RC}} = – 1 = \frac{{{U_L}}}{{{U_R}}}.\frac{{ – {U_C}}}{{{U_R}}} = – 1 \Rightarrow {U_L}{U_C} = U_R^2.\) Do đó: \({\left( {{U_L}{U_C}} \right)^2} = \left( {{{300}^2} – U_R^2} \right)\left( {{{400}^2} – U_R^2} \right) = U_R^4 \Rightarrow {U_R} = 240\left( {\text{V}} \right).\) Bình luận: Cách giải này khó ở chỗ là giải phương trình bậc 4 của R.Cách 2: Dùng phương pháp giản đồ vectơ buộc*Bài toán liên quan đến điện áp bắt chéo nên ta tổng hợp theo quy tắc hình bình hành các vecto điện áp \(\left\{ {\begin{array}{*{20}{c}} {{{\overrightarrow U }_{AN}} = {{\overrightarrow U }_R} + {{\overrightarrow U }_L}} \\ {{{\overrightarrow U }_{MB}} = {{\overrightarrow U }_R} + {{\overrightarrow U }_C}} \end{array}} \right..\) Do \({\overrightarrow U _{AN}} \bot {\overrightarrow U _{NB}},\) nên \(\Delta O{U_{AN}}{U_{MB}}\) vuông.Suy ra \(\frac{1}{{U_R^2}} = \frac{1}{{U_{AN}^2}} + \frac{1}{{U_{MB}^2}}.\) Hay \(\frac{1}{{U_R^2}} = \frac{1}{{{{300}^2}}} + \frac{1}{{{{400}^2}}} \Leftrightarrow {U_R} = 240\left( {\text{V}} \right).\)\({\text{7,5m/s}}\).
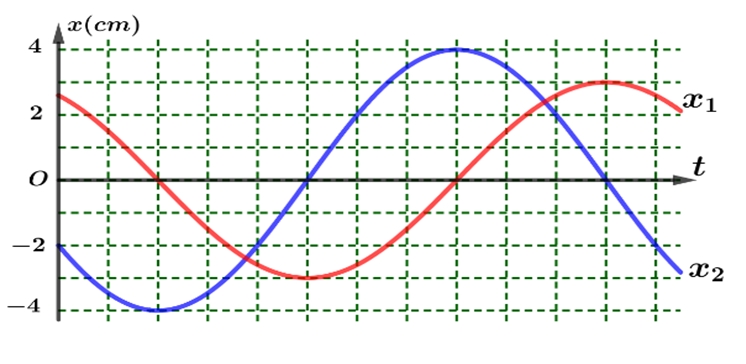 Theo phương pháp giản đồ Fre-nen, dao động của vật được biểu diễn bởi một vectơ quay. Biết tốc độ góc của vectơ này là \(\frac{{5\pi }}{3}rad/s\). Động năng của vật ở thời điểm \(t = 0,2\,s\) bằng
Theo phương pháp giản đồ Fre-nen, dao động của vật được biểu diễn bởi một vectơ quay. Biết tốc độ góc của vectơ này là \(\frac{{5\pi }}{3}rad/s\). Động năng của vật ở thời điểm \(t = 0,2\,s\) bằng\(5 mJ\).
\({2.10^{ - 3}}A\).
6, 04 tỉ năm.
-12,5.
\(13\).
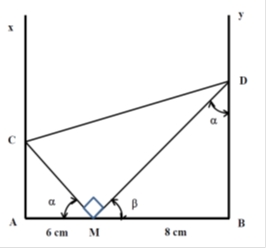
Ta có: \({S_{\left( {CMD} \right)}} = \frac{1}{2} \cdot MC.MD,\) để \({S_{\left( {CMD} \right)}}_{\min } \Leftrightarrow \alpha = 45^\circ \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{CA = 6\;cm.} \\
{BD = 8\;cm.}
\end{array}} \right..\)
\( \Rightarrow {k_M} = \frac{{MA – MB}}{\lambda } = \frac{{6 – 8}}{{0,9}} = – 2,22.\)
\( \Rightarrow {k_D} = \frac{{DA – DB}}{\lambda } = \frac{{\sqrt {{{14}^2} + {8^2}} – 8}}{{0,9}} = 9,02.\)
Số cực đại trên \(MD\) là \({k_M} \leqslant k \leqslant {k_D} \Leftrightarrow – 2,22 \leqslant k \leqslant 9,02 \Rightarrow 12.\)cực đại.
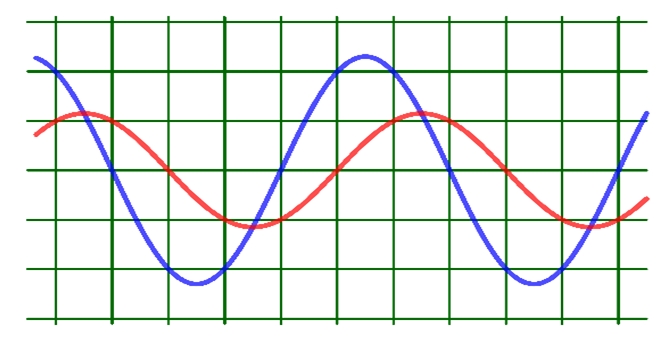
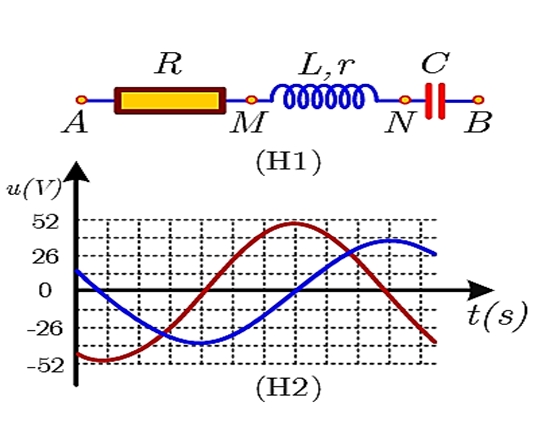 Hình H2 là đồ thị biểu diễn sự phụ thuộc của điện áp uAB giữa hai điểm A và B, và điện áp uMN giữa hai điểm M và N theo thời gian t.. Biết 63RCω= 16 và r = 5 . Công suất tiêu thụ của đoạn mạch AB là
Hình H2 là đồ thị biểu diễn sự phụ thuộc của điện áp uAB giữa hai điểm A và B, và điện áp uMN giữa hai điểm M và N theo thời gian t.. Biết 63RCω= 16 và r = 5 . Công suất tiêu thụ của đoạn mạch AB là24W.
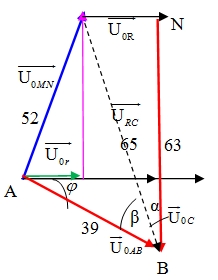 Dùng giản đồ vec tơ: Đề cho : \({Z_C} = \frac{{63}}{{16}}R\)=> \(\tan \alpha = \frac{R}{{{Z_C}}} = \frac{{16}}{{63}} = > \cos \alpha = \frac{{63}}{{65}}.\)Tính: \({U_{RC}} = \sqrt {U_{AB}^2 + U_{MN}^2} = \sqrt {{{39}^2} + {{52}^2}} = 65V.\).\({U_{0C}} = {U_{0RC}}\cos \alpha = 65.\frac{{63}}{{65}} = 63V;\);\({U_{0R}} = {U_{0RC}}\tan \alpha = 63.\frac{{16}}{{63}} = 16V.\)\(\cos \varphi = \cos (\frac{\pi }{2} – (\alpha + \beta )) = \cos (\frac{\pi }{2} – {\tan ^{ – 1}}(\frac{{16}}{{63}}) – {\tan ^{ – 1}}(\frac{{52}}{{39}}) = \frac{{12}}{{13}}.\)\({U_{0r}} + {U_{0R}} = {U_{AB}}\cos \varphi = 39.\frac{{12}}{{13}} = 36V = > {U_{0r}} = 36 – {U_{0R}} = 36 – 16 = 20V\)\( = > {I_0} = \frac{{{U_{0r}}}}{r} = \frac{{20}}{5} = 4A;R = \frac{{{U_{0R}}}}{{{I_0}}} = \frac{{16}}{4} = 4\Omega .\)\(P = {I^2}(R + r) = \frac{{I_0^2}}{2}(R + r) = \frac{{{4^2}}}{2}(4 + 5) = 72W.\) Hay:\(P = UI\cos \varphi = \frac{{{U_0}.{I_0}}}{2}\cos \varphi = \frac{{39}}{2}.\frac{4}{1}.\frac{{12}}{{13}} = 72W.\). Cách 2: Ta thấy đoạn MN có L và r, đoạn AB có tụ C nên uMN luôn sớm pha hơn uAB \( \to \left\{ {\begin{array}{*{20}{l}} {{U_{0AB}} = 39V} \\ {{U_{0MN}} = 52V} \end{array}\;} \right.\)Theo bài \(63RC\omega = 16 \to {Z_{\text{C}}} = \frac{{63}}{{16}}R \to {U_{\text{c}}} = \frac{{63}}{{16}}{U_R}. & \left( 1 \right).\)Một chu kỳ ứng với 12 ô, nên uMN sớm pha hơn uAB một góc \(\frac{\pi }{2}rad\) \(\overrightarrow {{U_{AB}}} = \overrightarrow {{U_{MN}}} + \overrightarrow {{U_{RC}}} \to {U_{oRC}} = \sqrt {U_{oAB}^2 + U_{oMN}^2} = 65(V)\); mà \(U_{oRC}^2 = U_{oR}^2 + U_{oC}^2\) Từ và ta có UOC=63V; UoR=16V => \({U_R} = \frac{{{U_{0R}}}}{{\sqrt 2 }} = \frac{{16}}{{\sqrt 2 }} = 8\sqrt 2 \;V.\)Giải hệ \(\left\{ \begin{gathered} {52^2} = U_{{\text{or}}}^{\text{2}} + U_{oL}^2 \hfill \\ {39^2} = {(16 + {U_{{\text{or}}}})^2} + {({U_{oL}} – 63)^2} \hfill \\ \end{gathered} \right. \to {U_{or}} = 20(V) \to {U_r} = 10\sqrt 2 (V).\)\( \to I = \frac{{{U_r}}}{r} = \frac{{10\sqrt 2 }}{5} = 2\sqrt 2 (A)\)\( \to R = \frac{{{U_R}}}{I} = 4\Omega \to {P_{AB}} = \left( {R + r} \right){I^2} = 72(W)\)
Dùng giản đồ vec tơ: Đề cho : \({Z_C} = \frac{{63}}{{16}}R\)=> \(\tan \alpha = \frac{R}{{{Z_C}}} = \frac{{16}}{{63}} = > \cos \alpha = \frac{{63}}{{65}}.\)Tính: \({U_{RC}} = \sqrt {U_{AB}^2 + U_{MN}^2} = \sqrt {{{39}^2} + {{52}^2}} = 65V.\).\({U_{0C}} = {U_{0RC}}\cos \alpha = 65.\frac{{63}}{{65}} = 63V;\);\({U_{0R}} = {U_{0RC}}\tan \alpha = 63.\frac{{16}}{{63}} = 16V.\)\(\cos \varphi = \cos (\frac{\pi }{2} – (\alpha + \beta )) = \cos (\frac{\pi }{2} – {\tan ^{ – 1}}(\frac{{16}}{{63}}) – {\tan ^{ – 1}}(\frac{{52}}{{39}}) = \frac{{12}}{{13}}.\)\({U_{0r}} + {U_{0R}} = {U_{AB}}\cos \varphi = 39.\frac{{12}}{{13}} = 36V = > {U_{0r}} = 36 – {U_{0R}} = 36 – 16 = 20V\)\( = > {I_0} = \frac{{{U_{0r}}}}{r} = \frac{{20}}{5} = 4A;R = \frac{{{U_{0R}}}}{{{I_0}}} = \frac{{16}}{4} = 4\Omega .\)\(P = {I^2}(R + r) = \frac{{I_0^2}}{2}(R + r) = \frac{{{4^2}}}{2}(4 + 5) = 72W.\) Hay:\(P = UI\cos \varphi = \frac{{{U_0}.{I_0}}}{2}\cos \varphi = \frac{{39}}{2}.\frac{4}{1}.\frac{{12}}{{13}} = 72W.\). Cách 2: Ta thấy đoạn MN có L và r, đoạn AB có tụ C nên uMN luôn sớm pha hơn uAB \( \to \left\{ {\begin{array}{*{20}{l}} {{U_{0AB}} = 39V} \\ {{U_{0MN}} = 52V} \end{array}\;} \right.\)Theo bài \(63RC\omega = 16 \to {Z_{\text{C}}} = \frac{{63}}{{16}}R \to {U_{\text{c}}} = \frac{{63}}{{16}}{U_R}. & \left( 1 \right).\)Một chu kỳ ứng với 12 ô, nên uMN sớm pha hơn uAB một góc \(\frac{\pi }{2}rad\) \(\overrightarrow {{U_{AB}}} = \overrightarrow {{U_{MN}}} + \overrightarrow {{U_{RC}}} \to {U_{oRC}} = \sqrt {U_{oAB}^2 + U_{oMN}^2} = 65(V)\); mà \(U_{oRC}^2 = U_{oR}^2 + U_{oC}^2\) Từ và ta có UOC=63V; UoR=16V => \({U_R} = \frac{{{U_{0R}}}}{{\sqrt 2 }} = \frac{{16}}{{\sqrt 2 }} = 8\sqrt 2 \;V.\)Giải hệ \(\left\{ \begin{gathered} {52^2} = U_{{\text{or}}}^{\text{2}} + U_{oL}^2 \hfill \\ {39^2} = {(16 + {U_{{\text{or}}}})^2} + {({U_{oL}} – 63)^2} \hfill \\ \end{gathered} \right. \to {U_{or}} = 20(V) \to {U_r} = 10\sqrt 2 (V).\)\( \to I = \frac{{{U_r}}}{r} = \frac{{10\sqrt 2 }}{5} = 2\sqrt 2 (A)\)\( \to R = \frac{{{U_R}}}{I} = 4\Omega \to {P_{AB}} = \left( {R + r} \right){I^2} = 72(W)\)