Đề Kiểm Tra Thường Xuyên Bài Hàm Số Bậc Hai Lời Giải-Đề 8
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-kiem-tra-thuong-xuyen-bai-ham-so-bac-hai-loi-giai-de-8
Đề Kiểm Tra: Đề Kiểm Tra Thường Xuyên Bài Hàm Số Bậc Hai Lời Giải-Đề 8
Câu 1:
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?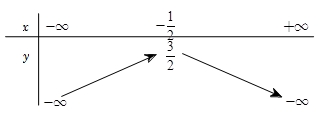

\(y = - 2{x^2} - 2x + 1.\)
Bảng biến thiên có bề lõm hướng xuống. Loại đáp án A và B.
Đỉnh của parabol có tọa độ là \(\left( { – \frac{1}{2};\frac{3}{2}} \right)\).
Xét các đáp án còn lại, đáp án D thỏa mãn.
Đỉnh của parabol có tọa độ là \(\left( { – \frac{1}{2};\frac{3}{2}} \right)\).
Xét các đáp án còn lại, đáp án D thỏa mãn.
Câu 2:
Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. 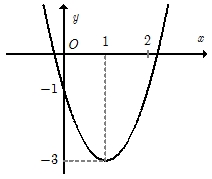 Hỏi hàm số đó là hàm số nào?
Hỏi hàm số đó là hàm số nào?
 Hỏi hàm số đó là hàm số nào?
Hỏi hàm số đó là hàm số nào?\(y = 2{x^2} - 4x - 1.\)
Parabol có bề lõm hướng lên. Loại đáp án C.
Đỉnh của parabol là điểm \(\left( {1; – 3} \right)\).
Xét các đáp án A, B và D, đáp án B thỏa mãn.
Đỉnh của parabol là điểm \(\left( {1; – 3} \right)\).
Xét các đáp án A, B và D, đáp án B thỏa mãn.
Câu 3:
Parabol\(y = a{x^2} + bx + c\) đi qua \(A\left( {0; – 1} \right)\), \(B\left( {1; – 1} \right)\), \(C\left( { – 1;1} \right)\) có phương trình là
\(y = {x^2} - x - 1\).
Ta có: Vì \(A,B,C \in (P)\)\( \Leftrightarrow \left\{ \begin{gathered} – 1 = a{.0^2} + b.0 + c \hfill \\ – 1 = a.{\left( 1 \right)^2} + b.(1) + c \hfill \\ 1 = a.{\left( { – 1} \right)^2} + b.( – 1) + c \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} a = 1 \hfill \\ b = – 1 \hfill \\ c = – 1 \hfill \\ \end{gathered} \right.\).
Vậy \(\left( P \right):y = {x^2} – x – 1\).
Vậy \(\left( P \right):y = {x^2} – x – 1\).
Câu 4:
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ dưới đây. Khẳng định nào sau đây là đúng?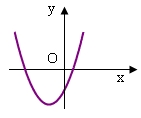

\(a > 0,b > 0,c < 0\).
Đồ thị hàm số cắt trục \(Oy\) tại điểm nằm phía dưới trục \(Ox\) nên \(c < 0\)
Đồ thị có bề lõm hướng lên do đó \(a > 0\)
Tọa độ đỉnh nằm ở góc phần tư thứ III nên \(\frac{{ – b}}{{2a}} < 0\)\( \Rightarrow b > 0\).
Đồ thị có bề lõm hướng lên do đó \(a > 0\)
Tọa độ đỉnh nằm ở góc phần tư thứ III nên \(\frac{{ – b}}{{2a}} < 0\)\( \Rightarrow b > 0\).
Câu 5:
Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau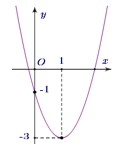 Phương trình của parabol này là
Phương trình của parabol này là
 Phương trình của parabol này là
Phương trình của parabol này là\(y = 2{x^2} - 4x - 1\).
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, – 1} \right)\) nên \(c = – 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, – 3} \right)\), ta có phương trình: \(\left\{ \begin{gathered} – \frac{b}{{2a}} = 1 \hfill \\ a{.1^2} + b.1 – 1 = – 3 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow \left\{ \begin{gathered} 2a + b = 0 \hfill \\ a + b = – 2 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow \left\{ \begin{gathered} a = 2 \hfill \\ b = – 4 \hfill \\ \end{gathered} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} – 4x – 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, – 3} \right)\), ta có phương trình: \(\left\{ \begin{gathered} – \frac{b}{{2a}} = 1 \hfill \\ a{.1^2} + b.1 – 1 = – 3 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow \left\{ \begin{gathered} 2a + b = 0 \hfill \\ a + b = – 2 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow \left\{ \begin{gathered} a = 2 \hfill \\ b = – 4 \hfill \\ \end{gathered} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} – 4x – 1\).
Câu 6:
Đồ thị hình bên dưới là đồ thị của hàm số bậc hai nào?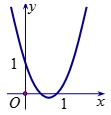

\(y = 2{x^2} - 3x + 1\).
Dựa vào hình vẽ ta có hàm số bậc hai có hệ số \(a > 0\) nên ta loại đáp án C,D.
Mặt khác đồ thị hàm số cắt trục hoành tại điểm có tọa độ \(\left( {1;0} \right)\), mà điểm \(\left( {1;0} \right)\) thuộc đồ thị hàm số \(y = 2{x^2} – 3x + 1\) và không thuộc đồ thị hàm số \(y = {x^2} – 3x + 1\)
Mặt khác đồ thị hàm số cắt trục hoành tại điểm có tọa độ \(\left( {1;0} \right)\), mà điểm \(\left( {1;0} \right)\) thuộc đồ thị hàm số \(y = 2{x^2} – 3x + 1\) và không thuộc đồ thị hàm số \(y = {x^2} – 3x + 1\)
Câu 7:
Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. 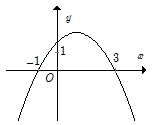 Hỏi hàm số đó là hàm số nào?
Hỏi hàm số đó là hàm số nào?
 Hỏi hàm số đó là hàm số nào?
Hỏi hàm số đó là hàm số nào?\(y = - \frac{1}{2}{x^2} + x + \frac{3}{2}.\)
Parabol có bề lõm hướng xuống. Loại đáp án A, C.
Parabol cắt trục hoành tại 2 điểm \(\left( {3;0} \right)\) và \(\left( { – 1;0} \right)\).
Xét các đáp án B và D, đáp án D thỏa mãn.
Parabol cắt trục hoành tại 2 điểm \(\left( {3;0} \right)\) và \(\left( { – 1;0} \right)\).
Xét các đáp án B và D, đáp án D thỏa mãn.
Câu 8:
Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. 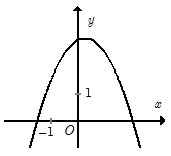 Hỏi hàm số đó là hàm số nào?
Hỏi hàm số đó là hàm số nào?
 Hỏi hàm số đó là hàm số nào?
Hỏi hàm số đó là hàm số nào?\(y = - {x^2} + \frac{1}{2}x + 3.\)
Bề lõm quay xuống nên loại C.Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt nên loại A.
Vì phương trình hoành độ giao điểm của đáp án A là \( – 2{x^2} + x – 1 = 0\) vô nghiệm.
Xét phương trình hoành độ giao điểm của đáp án B, ta có \( – 2{x^2} + x + 3 = 0 \Leftrightarrow \left[ \begin{gathered} x = – 1 \hfill \\ x = \frac{3}{2} \hfill \\ \end{gathered} \right.\).
Quan sát đồ thị ta thấy đồ thị hàm số không cắt trục hoành tại điểm có hoành độ bằng \( – 1.\) Do đó đáp án B không phù hợp.
Dùng phương pháp loại trừ, thì D là đáp án đúng.
Vì phương trình hoành độ giao điểm của đáp án A là \( – 2{x^2} + x – 1 = 0\) vô nghiệm.
Xét phương trình hoành độ giao điểm của đáp án B, ta có \( – 2{x^2} + x + 3 = 0 \Leftrightarrow \left[ \begin{gathered} x = – 1 \hfill \\ x = \frac{3}{2} \hfill \\ \end{gathered} \right.\).
Quan sát đồ thị ta thấy đồ thị hàm số không cắt trục hoành tại điểm có hoành độ bằng \( – 1.\) Do đó đáp án B không phù hợp.
Dùng phương pháp loại trừ, thì D là đáp án đúng.
Câu 9:
Hàm số \(y = – {x^2} + 2x + m – 4\) đạt giá trị lớn nhất trên đoạn \(\left[ { – 1;2} \right]\) bằng \(3\) khi \(m\) thuộc
\(\left( {5;7} \right)\).
Xét hàm số \(y = – {x^2} + 2x + m – 4\) trên đoạn \(\left[ { – 1;2} \right]\).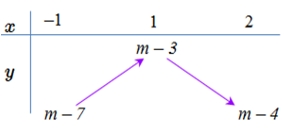 Hàm số đạt GTLN trên đoạn \(\left[ { – 1;2} \right]\) bằng \(3\) khi và chỉ khi \(m – 3 = 3\) \( \Leftrightarrow m = 6\).
Hàm số đạt GTLN trên đoạn \(\left[ { – 1;2} \right]\) bằng \(3\) khi và chỉ khi \(m – 3 = 3\) \( \Leftrightarrow m = 6\).
 Hàm số đạt GTLN trên đoạn \(\left[ { – 1;2} \right]\) bằng \(3\) khi và chỉ khi \(m – 3 = 3\) \( \Leftrightarrow m = 6\).
Hàm số đạt GTLN trên đoạn \(\left[ { – 1;2} \right]\) bằng \(3\) khi và chỉ khi \(m – 3 = 3\) \( \Leftrightarrow m = 6\).Câu 10:
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là \(4m\) còn kích thước cửa ở giữa là \(3m \times 4m\). Hãy tính khoảng cách giữa hai điểm \(A\) và \(B\).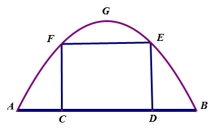

\(8m\).
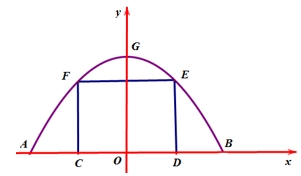 Gắn hệ trục tọa độ \(Oxy\) như hình vẽ, chiếc cổng là 1 phần của parabol \((P)\): \(y = a{x^2} + bx + c\) với \(a < 0\).
Gắn hệ trục tọa độ \(Oxy\) như hình vẽ, chiếc cổng là 1 phần của parabol \((P)\): \(y = a{x^2} + bx + c\) với \(a < 0\).Do parabol \((P)\) đối xứng qua trục tung nên có trục đối xứng \(x = 0 \Rightarrow – \frac{b}{{2a}} = 0 \Leftrightarrow b = 0\).
Chiều cao của cổng parabol là \(4m\) nên \(G(0;4)\) \( \Rightarrow c = 4\).\( \Rightarrow (P):y = a{x^2} + 4\)
Lại có, kích thước cửa ở giữa là \(3m \times 4m\) nên \(E(2;3),\,F( – 2;3)\).
Thay tạo độ điểm \(E(2;3)\) vào phương trình \((P)\) ta được\(3 = a{.2^2} + 4 \Leftrightarrow a = – \frac{1}{4}\).
Vậy \((P):y = – \frac{1}{4}{x^2} + 4\).Ta có \( – \frac{1}{4}{x^2} + 4 = 0 \Leftrightarrow \left[ \begin{gathered} x = 4 \hfill \\ x = – 4 \hfill \\ \end{gathered} \right.\) nên \(A( – 4;0),\,B(4;0)\).
Giải thích & Đáp án chi tiết
Câu 1
Đáp án đúng: ʍ
\(y = - 2{x^2} - 2x + 1.\)
Câu 2
Đáp án đúng: ʋ
\(y = 2{x^2} - 4x - 1.\)
Câu 3
Đáp án đúng: ʋ
\(y = {x^2} - x - 1\).
Câu 4
Đáp án đúng: ʋ
\(a > 0,b > 0,c < 0\).
Câu 5
Đáp án đúng: ʍ
\(y = 2{x^2} - 4x - 1\).
Câu 6
Đáp án đúng: ʋ
\(y = 2{x^2} - 3x + 1\).
Câu 7
Đáp án đúng: ʍ
\(y = - \frac{1}{2}{x^2} + x + \frac{3}{2}.\)
Câu 8
Đáp án đúng: ʍ
\(y = - {x^2} + \frac{1}{2}x + 3.\)
Câu 9
Đáp án đúng: ʌ
\(\left( {5;7} \right)\).
Câu 10
Đáp án đúng: ʍ
\(8m\).
