Kiểm Tra 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Đáp Án Và Lời Giải-Đề 3
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/kiem-tra-15-phut-bai-16-ham-so-bac-hai-online-co-dap-an-va-loi-giai-de-3
Đề Kiểm Tra: Kiểm Tra 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Đáp Án Và Lời Giải-Đề 3
Câu 1:
Khoảng nghịch biến của hàm số \(y = {x^2} – 4x + 3\)là
\(\left( { - \infty ;2} \right)\).
Hàm số \(y = {x^2} – 4x + 3\) có hệ số \(a = 1 > 0\) nên đồng biến trên khoảng \(\left( { – \infty ; – \frac{b}{{2a}}} \right)\).Vì vậy hàm số đồng biến trên \(\left( { – \infty ;2} \right)\).
Câu 2:
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = {x^2} – 2\left( {m + 1} \right)x – 3\) đồng biến trên khoảng \(\left( {4;2024} \right)\)?
3
Hàm số có \(a = 1 > 0,\frac{{ – b}}{{2a}} = m + 1\) nên đồng biến trên khoảng \(\left( {m + 1; + \infty } \right)\).Do đó để hàm số đồng biến trên khoảng \(\left( {4;2024} \right)\) thì ta phải có\(\left( {4;2024} \right) \subset \left( {m + 1; + \infty } \right) \Leftrightarrow m + 1 \leqslant 4 \Leftrightarrow m \leqslant 3\).Vậy có ba giá trị nguyên dương của m thỏa mãn yêu cầu bài toán là 1, 2, 3.
Câu 3:
Cho parabol \(\left( P \right):y = 3{x^2} – 2x + 1\). Điểm nào sau đây là đỉnh của \(\left( P \right)\)?
\(I\left( {\frac{1}{3};\,\frac{2}{3}} \right)\).
Hoành độ đỉnh của \(\left( P \right):y = 3{x^2} – 2x + 1\) là \(x = – \frac{b}{{2a}} = \frac{1}{3}\)\( \Rightarrow y = 3{\left( {\frac{1}{3}} \right)^2} – 2.\frac{1}{3} + 1 = \frac{2}{3}\).Vậy \(I\left( {\frac{1}{3};\,\frac{2}{3}} \right)\).
Câu 4:
Parabol \(y = – {x^2} + 2x + 3\) có phương trình trục đối xứng là
\(x = 1\).
Parabol \(10m\) có trục đối xứng là đường thẳng \(\left\{ \begin{gathered} x + 2 \geqslant 0 \hfill \\ x – 5 \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x \geqslant – 2 \hfill \\ x \ne 5 \hfill \\ \end{gathered} \right.\) \(\left[ { – 2; + \infty } \right)\).
Câu 5:
Cho Parabol: \(y = a{x^2} + bx + c\) có đỉnh \(I(2;0)\) và \((P)\) cắt trục \(Oy\) tại điểm \(M(0; – 1)\). Khi đó Parabol có hàm số là
\((P):y = - \frac{1}{4}{x^2} + x - 1\).
Parabol \(\left( P \right):y = a{x^2} + bx + c\xrightarrow{{}}\) đỉnh \(I\left( { – \frac{b}{{2a}};c – \frac{{{b^2}}}{{4a}}} \right)\)
Theo bài ra, ta có có đỉnh \(I(2;0) \Rightarrow \left\{ \begin{gathered}
– \frac{b}{{2a}} = 2 \hfill \\
c – \frac{{{b^2}}}{{4a}} = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
b = – 4a \hfill \\
{b^2} = 4ac \hfill \\
\end{gathered} \right.\,\,\,(1)\)
Theo bài ra, ta có có đỉnh \(I(2;0) \Rightarrow \left\{ \begin{gathered}
– \frac{b}{{2a}} = 2 \hfill \\
c – \frac{{{b^2}}}{{4a}} = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
b = – 4a \hfill \\
{b^2} = 4ac \hfill \\
\end{gathered} \right.\,\,\,(1)\)
Câu 6:
Bảng biến thi của hàm số \(y = – 2{x^4} + 4x + 1\) là bảng nào sau đây?
<img src="https://tailieuhoctap.sachtruyen.com.vn/anh-dap-an-trac-nghiem/kiem-tra-15-phut-bai-16-ham-so-bac-hai-online-co-dap-an-va-loi-giai-de-3-5-2-0.jpg" alt="Kiểm Tra 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Đáp Án Và Lời Giải-Đề 3" class="mx-auto my-5 rounded-lg shadow-sm max-w-full h-auto" style="max-height: 350px;">.
Hàm số \(y = – 2{x^4} + 4x + 1\) có hệ số \(a = – 2 < 0\) nên bề lõm quay lên trên vì vậy ta loại đáp án B,D Hàm số có tọa độ đỉnh \(I(1;3)\) nên ta loại đáp án AVậy bảng biến thiên của hàm số \(y = - 2{x^4} + 4x + 1\) là bảng C
Câu 7:
Cho hàm số \(y = a{x^2} + bx + c,\,(a > 0,\,b < 0,\,c > 0)\)thì đồ thị của hàm số là hình nào trong các hình sau: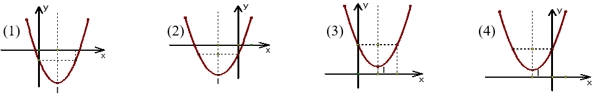
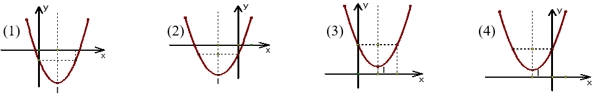
Hình (3).
Vì \(c > 0\)nên đồ thị cắt trục tung tại điểm nằm phía trên trục hoành.Mặt khác \(a > 0,\,b < 0\) nên hai hệ số này trái dấu, trục đối xứng sẽ phía phải trục tung.Do đó, hình là đáp án cần tìm.
Câu 8:
Cho hàm số \(y = a{x^2} + bx + c,\,\left( {a \ne 0} \right)\) có bảng biến thiên trên nửa khoảng \(\left[ {0; + \infty } \right)\) như hình vẽ dưới đây: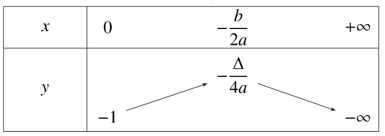 Xác định dấu của \(a\), \(b\), \(c\).
Xác định dấu của \(a\), \(b\), \(c\).
 Xác định dấu của \(a\), \(b\), \(c\).
Xác định dấu của \(a\), \(b\), \(c\).\(a < 0,b > 0,c < 0\).
Dựa vào bảng biến thiên ta có: Parabol \(\left( P \right)\) có bề lõm quay xuống dưới; hoành độ đỉnh dương;cắt trục tung tại điểm có tung độ bằng – 1 nên \(\left\{ \begin{gathered} a < 0 \hfill \\ \frac{{ - b}}{{2a}} > 0 \hfill \\ c = – 1 < 0 \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} a < 0 \hfill \\ b > 0 \hfill \\ c < 0 \hfill \\ \end{gathered} \right.\).
Câu 9:
Giá trị nhỏ nhất của hàm số \(y = {x^2} + 2x + 3\) đạt được tại
\(x = - 1\).
Ta có: \(y = {x^2} + 2x + 3 = {(x + 1)^2} + 2 \geqslant 2\,,\,\forall x \in \mathbb{R}\)Dấu bằng xảy ra khi \(x = – 1\) nên chọn đáp án B
Câu 10:
Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ \(Oth\), trong đó \(t\) là thời gian kể từ khi quả bóng được đá lên; h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao \(1,2m\). Sau đó \(\;1\) giây, nó đạt độ cao \(8,5m\) và \(2\) giây sau khi đá lên, nó đạt độ cao 6m. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên kể từ khi quả bóng được đá lên, \(h\) là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao \(1,2m\) và sau \(1\) giây thì nó đạt độ cao \(8,5m\), sau \(2\) giây nó đạt độ cao \(6m\). Tính \(10a + 5b + 5c\).
\(10a + 5b + 5c = 18\).
Từ giả thiết của bài toán ta có hệ phương trình\(\left\{ \begin{gathered} c = 1,2 \hfill \\ a + b + c = 8,5 \hfill \\ 4a + 2b + c = 6 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} a = – \frac{{49}}{{10}} \hfill \\ b = \frac{{61}}{5} \hfill \\ c = 1,2 \hfill \\ \end{gathered} \right.\)\( \Rightarrow 10a + 5b + 5c = 18\).
Giải thích & Đáp án chi tiết
Câu 1
Đáp án đúng: ʌ
\(\left( { - \infty ;2} \right)\).
Câu 2
Đáp án đúng: ʍ
3
Câu 3
Đáp án đúng: ʋ
\(I\left( {\frac{1}{3};\,\frac{2}{3}} \right)\).
Câu 4
Đáp án đúng: ʌ
\(x = 1\).
Câu 5
Đáp án đúng: ʌ
\((P):y = - \frac{1}{4}{x^2} + x - 1\).
Câu 6
Đáp án đúng: ʌ
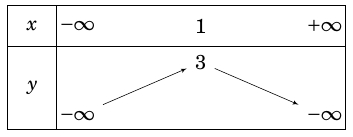 .
.Câu 7
Đáp án đúng: ʌ
Hình (3).
Câu 8
Đáp án đúng: ʍ
\(a < 0,b > 0,c < 0\).
Câu 9
Đáp án đúng: ʋ
\(x = - 1\).
Câu 10
Đáp án đúng: ʌ
\(10a + 5b + 5c = 18\).
