Kiểm Tra Thường Xuyên Bài 16 Hàm Số Bậc Hai Có Đáp Án Và Lời Giải-Đề 7
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/kiem-tra-thuong-xuyen-bai-16-ham-so-bac-hai-co-dap-an-va-loi-giai-de-7
Đề Kiểm Tra: Kiểm Tra Thường Xuyên Bài 16 Hàm Số Bậc Hai Có Đáp Án Và Lời Giải-Đề 7
Câu 1:
Tìm tất cả các giá trị dương của tham số \(m\) để hàm số \(f\left( x \right) = m{x^2} – 4x – {m^2}\) luôn nghịch biến trên \(\left( { – 1;2} \right)\).
\(0 < m \leqslant 1\).
– Với \(m > 0\), ta có hàm số \(f\left( x \right) = m{x^2} – 4x – {m^2}\) nghịch biến trên \(\left( { – \infty ;\frac{2}{m}} \right)\), suy ra hàm nghịch biến trên \(\left( { – 1;2} \right)\) khi \(\left( { – 1;2} \right) \subset \left( { – \infty ;\frac{2}{m}} \right) \Leftrightarrow 2 \leqslant \frac{2}{m} \Leftrightarrow 0 < m \leqslant 1\).
Câu 2:
Tìm giá trị của tham số \(m\) để đỉnh \(I\) của đồ thị hàm số \(y = – {x^2} + 6x + m\) thuộc đường thẳng \(y = x + 2024\).
\(m = 2018\).
Đồ thị hàm số \(y = – {x^2} + 6x + m\) là parabol có đỉnh \(I\left( {3;9 + m} \right)\).
Đỉnh \(I\left( {3;9 + m} \right)\) thuộc đường thẳng \(y = x + 2024 \Leftrightarrow 9 + m = 3 + 2024 \Leftrightarrow m = 2018\).
Đỉnh \(I\left( {3;9 + m} \right)\) thuộc đường thẳng \(y = x + 2024 \Leftrightarrow 9 + m = 3 + 2024 \Leftrightarrow m = 2018\).
Câu 3:
Cho parabol \((p):y = a{x^2} + bx + c\) có trục đối xứng là đường thẳng \(x = 1\). Khi đó \(4a + 2b\) bằng
\(0\).
Do parabol \(H\):\(AB\) có trục đối xứng là đường thẳng \(AB = 10\) nên \(y = – \frac{1}{3}{x^2}\) \(HA = HB = 5\)\(B\left( {{x_B};{y_B}} \right) \Rightarrow {x_B} = 5 \Rightarrow {y_B} = – \frac{{25}}{3}\)\( \Rightarrow OH = \left| {{y_B}} \right| = \frac{{25}}{3}\).
Câu 4:
Parabol \(y = a{x^2} + bx + c\) đi qua \(A\left( {8;0} \right)\) và có đỉnh \(I\left( {6; – 12} \right)\). Khi đó tích \(a.b.c\) bằng
\( - 10368\).
Điều kiện \(a \ne 0.\)Từ giả thiết ta có hệ \(\left\{ \begin{gathered} 64a + 8b + c = 0 \hfill \\ 36a + 6b + c = – 12 \hfill \\ – \frac{b}{{2a}} = 6 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow \left\{ \begin{gathered} a = 3 \hfill \\ b = – 36 \hfill \\ c = 96 \hfill \\ \end{gathered} \right.\) \( \Rightarrow abc = – 10368\).
Câu 5:
Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau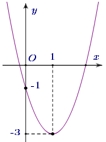 Phương trình của parabol này là
Phương trình của parabol này là
 Phương trình của parabol này là
Phương trình của parabol này là\(y = 2{x^2} - 4x - 1\).
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, – 1} \right)\) nên \(c = – 1\).
Câu 6:
Cho parabol \((P):y = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) có đồ thị như hình bên dưới.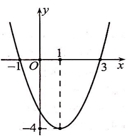 Khi đó \(2a + b + 2c\) có giá trị là:
Khi đó \(2a + b + 2c\) có giá trị là:
 Khi đó \(2a + b + 2c\) có giá trị là:
Khi đó \(2a + b + 2c\) có giá trị là:\( - 6\).
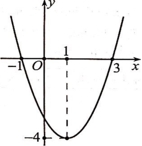 Parabol \((P):y = a{x^2} + bx + c,\;(a \ne 0)\) đi qua các điểm \(A( – 1;0),\;B(1; – 4),\;C(3;0)\)
Parabol \((P):y = a{x^2} + bx + c,\;(a \ne 0)\) đi qua các điểm \(A( – 1;0),\;B(1; – 4),\;C(3;0)\)Do đó ta có hệ phương trình:\(\left\{ \begin{gathered} a – b + c = 0 \hfill \\ a + b + c = – 4 \hfill \\ 9a + 3b + c = 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} a = 1 \hfill \\ b = – 2 \hfill \\ c = – 3 \hfill \\ \end{gathered} \right.\)
Khi đó: \(2a + b + 2c = 2.1 – 2 + 2( – 3) = – 6.\)
Câu 7:
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như bên.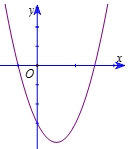 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?\(a > 0,b < 0,c < 0.\).
Đồ thị cắt trục tung tại điểm có tung độ \(\left( { = c} \right)\) âm nên \(c < 0\). Suy ra loại B,D.
Câu 8:
Đồ thị trong hình vẽ dưới đây là của hàm số nào trong các phương án A;B;C;D sau đây?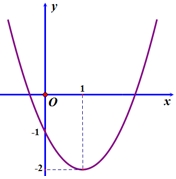

\(y = {x^2} - 2x - 1\).
Đồ thị cắt trục tung tại điểm có tung độ bằng \( – 1\) nên loại B và C
Hoành độ của đỉnh là \({x_I} = – \frac{b}{{2a}} = 1\) nên ta loại A và Chọn D
Hoành độ của đỉnh là \({x_I} = – \frac{b}{{2a}} = 1\) nên ta loại A và Chọn D
Câu 9:
Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau: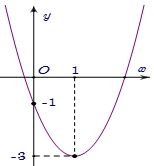 Phương trình của parabol này là
Phương trình của parabol này là
 Phương trình của parabol này là
Phương trình của parabol này là\(y = 2{x^2} - 4x - 1.\)
Do đồ thị cắt trục tung tại điểm có tung độ bằng \( – 1\) nên suy ra \(c = – 1\,\,\,\,\,\,\,(1)\)
Câu 10:
Giá trị lớn nhất của hàm số \(y = – 3{x^2} + 2x + 1\) trên đoạn \(\left[ {1;3} \right]\) là:
0
Ta có \( – \frac{b}{{2a}} = \frac{1}{3}\) và \(a = – 3 < 0\).
Giải thích & Đáp án chi tiết
Câu 1
Đáp án đúng: ʌ
\(0 < m \leqslant 1\).
Câu 2
Đáp án đúng: ʍ
\(m = 2018\).
Câu 3
Đáp án đúng: ʋ
\(0\).
Câu 4
Đáp án đúng: ʊ
\( - 10368\).
Câu 5
Đáp án đúng: ʍ
\(y = 2{x^2} - 4x - 1\).
Câu 6
Đáp án đúng: ʌ
\( - 6\).
Câu 7
Đáp án đúng: ʊ
\(a > 0,b < 0,c < 0.\).
Câu 8
Đáp án đúng: ʍ
\(y = {x^2} - 2x - 1\).
Câu 9
Đáp án đúng: ʍ
\(y = 2{x^2} - 4x - 1.\)
Câu 10
Đáp án đúng: ʋ
0
