Đề Kiểm Tra 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Lời Giải-Đề 5

Question 1

Câu 1:

Cho hàm số \(y = – {x^2} + 4x + 3.\) Chọn khẳng định đúng.

A
Hàm số đồng biến trên \(\mathbb{R}.\)
B
Hàm số nghịch biến trên \(\mathbb{R}.\)
C
Hàm số đồng biến trên \(\left( {2; + \infty } \right)\).
D
Hàm số nghịch biến trên \(\left( {2; + \infty } \right)\).

Do \(a = – 1\) nên hàm số đồng biến trên \(\left( { – \infty ;2} \right)\) nghịch biến trên \(\left( {2; + \infty } \right)\).

Answer

Hàm số nghịch biến trên \(\left( {2; + \infty } \right)\).

Question 2

Câu 2:

Hàm số \(y = – {x^2} + 2\left( {m – 1} \right)x + 3\) nghịch biến trên \(\left( {1; + \infty } \right)\) khi giá trị m thỏa mãn:

A
\(m \leqslant 0\).
B
\(m > 0\).
C
\(m \leqslant 2\).
D
\(0 < m \leqslant 2\)

Đồ thị hàm số có trục đối xứng là đường \(x = m – 1\).
Đồ thị hàm số đã cho có hệ số \({x^2}\) âm nên sẽ đồng biến trên \(\left( { – \infty ;m – 1} \right)\) và nghịch biến trên \(\left( {m – 1; + \infty } \right)\).
Theo đề, cần: \(m – 1 \leqslant 1 \Leftrightarrow m \leqslant 2\).

Answer

\(m \leqslant 2\).

Question 3

Câu 3:

Tọa độ đỉnh của parabol \(y = – 2{x^2} – 4x + 6\) là

A
\(I\left( { - 1;8} \right)\).
B
\(I\left( {1;0} \right)\).
C
\(I\left( {2; - 10} \right)\).
D
\(I\left( { - 1;6} \right)\).

Tọa độ đỉnh của parabol \(y = – 2{x^2} – 4x + 6\) là \(\left\{ \begin{gathered} x = – \frac{{ – 4}}{{2.\left( { – 2} \right)}} = – 1 \hfill \\ y = – 2.{\left( { – 1} \right)^2} – 4.\left( { – 1} \right) + 6 = 8 \hfill \\ \end{gathered} \right. \Rightarrow I\left( { – 1;8} \right)\).

Answer

\(I\left( { - 1;8} \right)\).

Question 4

Câu 4:

Cho Parabol \(\left( P \right):\,y = {x^2} + mx + n\) (\(m,\,n\) tham số). Xác định \(m,\,n\) để \(\left( P \right)\)nhận đỉnh \(I\left( {2;\, – 1} \right)\).

A
\(m = 4,\,n = - 3\).
B
\(m = 4,\,n = 3\).
C
\(m = - 4,\,n = - 3\).
D
\(m = - 4,\,n = 3\).

Parabol \(\left( P \right):\,y = {x^2} + mx + n\) nhận \(I\left( {2;\, – 1} \right)\) là đỉnh, khi đó ta có\(\left\{ \begin{gathered} 4 + 2m + n = – 1 \hfill \\ – \frac{m}{2} = 2 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} 2m + n = – 5 \hfill \\ m = – 4 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} n = 3 \hfill \\ m = – 4 \hfill \\ \end{gathered} \right.\).Vậy \(m = – 4,\,n = 3\).

Answer

\(m = - 4,\,n = 3\).

Question 5

Câu 5:

Gọi \(S\) là tập các giá trị \(m \ne 0\) để parabol \(\left( P \right):y = m{x^2} + 2mx + {m^2} + 2m\) có đỉnh nằm trên đường thẳng \(y = x + 7\). Tính tổng các giá trị của tập \(S\).

A
\( - 1\).
B
\(1\).
C
\(2\).
D
\( - 2\).

Khi \(m \ne 0\) thì \(\left( P \right):y = m{x^2} + 2mx + {m^2} + 2m\) có đỉnh là \(I\left( { – \frac{b}{{2a}}; – \frac{\Delta }{{4a}}} \right) \Rightarrow I\left( { – 1;{m^2} + m} \right)\)
Vì đỉnh nằm trên đường thẳng \(y = x + 7\) nên \({m^2} + m = – 1 + 7 \Leftrightarrow {m^2} + m – 6 = 0 \Leftrightarrow \left[ \begin{gathered} m = 2 \hfill \\ m = – 3 \hfill \\ \end{gathered} \right.\left( {TM} \right)\)
Vậy tổng các giá trị của tập \(S\): \(2 + \left( { – 3} \right) = – 1\).

Answer

<img src="https://tailieuhoctap.sachtruyen.com.vn/anh-dap-an-trac-nghiem/de-kiem-tra-15-phut-bai-16-ham-so-bac-hai-online-co-loi-giai-de-5-5-2-0.jpg" alt="Đề Kiểm Tra 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Lời Giải-Đề 5" class="mx-auto my-5 rounded-lg shadow-sm max-w-full h-auto" style="max-height: 350px;">.

Answer

\(a > 0,{\text{ }}b < 0,{\text{ }}c < 0\).

Answer

\(y = {x^2} - 4x\).

Answer

Hàm số \(y = - 3{x^2} + x + 2\) có giá trị lớn nhất bằng \(\frac{{25}}{{12}}\)

Question 6

Câu 6:

Bảng biến thiên nào dưới đây là của hàm số \(y = – {x^2} + 2x + 2\)?

A
B
C
.
D

\(y' = – 2x + 2\)\(y' = 0 \Leftrightarrow x = 1\)Hàm số đồng biến trên \(\left( { – \infty ;\,\;1} \right)\); nghịch biến trên \(\left( {1;\, + \infty } \right)\).

Question 7

Câu 7:

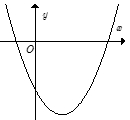
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng? Đề Kiểm Tra 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Lời Giải-Đề 5

A
\(a > 0,{\text{ }}b < 0,{\text{ }}c < 0\).
B
\(a > 0,{\text{ }}b < 0,{\text{ }}c > 0\).
C
\(a > 0,{\text{ }}b > 0,{\text{ }}c > 0\).
D
\(a < 0,{\text{ }}b < 0,{\text{ }}c < 0\).

Parabol có bề lõm quay lên \( \Rightarrow a > 0\) loại D
Parabol cắt trục tung tại điểm có tung độ âm nên \(c < 0\) loại B,C

Question 8

Câu 8:

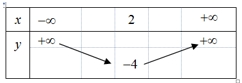
Bảng biến thiên sau là của hàm số nào? Đề Kiểm Tra 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Lời Giải-Đề 5

A
\(y = {x^2} - 4x\).
B
\(y = {x^2} + 4x\).
C
\(y = - {x^2} + 4x\).
D
\(y = - {x^2} - 4x\).

Từ bảng biến thiên suy ra hệ số \(a > 0\). Loại C, D
Toạ độ đỉnh \(I = \left( {2\,; – 4} \right)\) loại B

Question 9

Câu 9:

Khẳng định nào dưới đây đúng?

A
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị lớn nhất bằng \(\frac{{25}}{{12}}\)
B
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị nhỏ nhất bằng \(\frac{{25}}{{12}}\)
C
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị lớn nhất bằng \(\frac{{25}}{3}\)
D
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị nhỏ nhất bằng \(\frac{{25}}{3}\).

Ta có \(\Delta = {1^2} – 4.\left( { – 3} \right).2 = 25\)Vì \(a = – 3 < 0\) nên hàm số có giá trị lớn nhất là: \(\frac{{ - \Delta }}{{4a}} = \frac{{25}}{{12}}\).

Question 10

Câu 10:

Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao \(1m\) sau đó \(1\) giây nó đạt độ cao \(10m\) và \(3,5\) giây nó ở độ cao \(6,25m\). Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét?

A
\(11m\).
B
\(12m\).
C
\(13m\).
D
\(14m\).

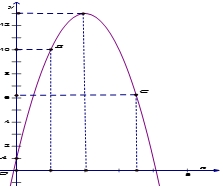Biết rằng quỹ đạo của quả bóng là một cung parabol nên phương trình có dạng \(y = a{x^2} + bx + c\)
Theo bài ra gắn vào hệ tọa độ và sẽ tương ứng các điểm \(A,\,B,\,C\) nên ta có\(\left\{ \begin{gathered} c = 1 \hfill \\ a + b + c = 10 \hfill \\ 12,25a + 3,5b + c = 6,25 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} a = – 3 \hfill \\ b = 12 \hfill \\ c = 1 \hfill \\ \end{gathered} \right.\).
Suy ra phương trình parabol là \(y = – 3{x^2} + 12x + 1\).
Parabol có đỉnh\(I(2;13)\).
Khi đó quả bóng đạt vị trí cao nhất tại đỉnh tức \(h = 13m\).

Đề Kiểm Tra 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Lời Giải-Đề 5

Đề Kiểm Tra: Đề Kiểm Tra 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Lời Giải-Đề 5

Giải thích & Đáp án chi tiết