Đề 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Lời Giải-Đề 4
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-15-phut-bai-16-ham-so-bac-hai-online-co-loi-giai-de-4
Đề Kiểm Tra: Đề 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Lời Giải-Đề 4
Câu 1:
Khoảng đồng biến của hàm số \(y = {x^2} – 4x + 3\) là
\(\left( {2; + \infty } \right)\).
Hàm số \(y = {x^2} – 4x + 3\)có \(a = 1 > 0\) nên đồng biến trên khoảng \(\left( { – \frac{b}{{2a}}; + \infty } \right)\).Vì vậy hàm số đồng biến trên \(\left( {2; + \infty } \right)\).
Câu 2:
Tìm tất cả các giá trị của \(b\) để hàm số \(y = {x^2} + 2(b + 6)x + 4\) đồng biến trên khoảng \(\left( {6; + \infty } \right)\).
\(b \geqslant - 12\).
Hàm số \(y = f(x) = {x^2} + 2(b + 6)x + 4\) là hàm số bậc hai có hệ sô \(a = 1 > 0\), \( – \frac{b}{{2a}} = – b – 6\)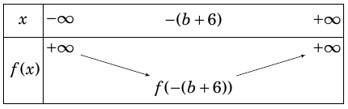 nên có bảng biến thiênTừ bảng biến thiên ta có:Hàm số đồng biến trên \(\left( {6; + \infty } \right)\)thì \( \Leftrightarrow \left( {6; + \infty } \right) \subset \left( { – b – 6; + \infty } \right) \Leftrightarrow – b – 6 \leqslant 6 \Leftrightarrow b \geqslant – 12.\).
nên có bảng biến thiênTừ bảng biến thiên ta có:Hàm số đồng biến trên \(\left( {6; + \infty } \right)\)thì \( \Leftrightarrow \left( {6; + \infty } \right) \subset \left( { – b – 6; + \infty } \right) \Leftrightarrow – b – 6 \leqslant 6 \Leftrightarrow b \geqslant – 12.\).
 nên có bảng biến thiênTừ bảng biến thiên ta có:Hàm số đồng biến trên \(\left( {6; + \infty } \right)\)thì \( \Leftrightarrow \left( {6; + \infty } \right) \subset \left( { – b – 6; + \infty } \right) \Leftrightarrow – b – 6 \leqslant 6 \Leftrightarrow b \geqslant – 12.\).
nên có bảng biến thiênTừ bảng biến thiên ta có:Hàm số đồng biến trên \(\left( {6; + \infty } \right)\)thì \( \Leftrightarrow \left( {6; + \infty } \right) \subset \left( { – b – 6; + \infty } \right) \Leftrightarrow – b – 6 \leqslant 6 \Leftrightarrow b \geqslant – 12.\).Câu 3:
Parabol \(\left( P \right):{\text{ }}y = – 2{x^2} – 6x + 3\) có hoành độ đỉnh là
\(x = - \frac{3}{2}\).
Parabol \(\left( P \right):{\text{ }}y = – 2{x^2} – 6x + 3\)có hoành độ đỉnh là \(x = – \frac{b}{{2a}}\)\( = – \frac{{ – 6}}{{2\left( { – 2} \right)}}\)\( = – \frac{3}{2}\).
Câu 4:
Cho hàm số \(y = a{x^2} + bx + c\,\,(a \ne 0)\) có đồ thị. Biết đồ thị của hàm số có đỉnh \(I(1;1)\) và đi qua điểm \(A(2;3)\). Tính tổng \(S = {a^2} + {b^2} + {c^2}\)
\(29\).
Vì đồ thị hàm số \(y = a{x^2} + bx + c\,\,(a \ne 0)\) có đỉnh \(I(1;1)\) và đi qua điểm \(A(2;3)\)
nên ta có hệ:\(\left\{ {\begin{array}{*{20}{c}} {a + b + c = 1} \\ {4a + 2b + c = 3} \\ { – \frac{b}{{2a}} = 1} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a + b + c = 1} \\ {4a + 2b + c = 3} \\ {2a + b = 0} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a = 2} \\ {b = – 4} \\ {c = 3} \end{array}} \right.\)
Nên \(S = {a^2} + {b^2} + {c^2}\)=29
nên ta có hệ:\(\left\{ {\begin{array}{*{20}{c}} {a + b + c = 1} \\ {4a + 2b + c = 3} \\ { – \frac{b}{{2a}} = 1} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a + b + c = 1} \\ {4a + 2b + c = 3} \\ {2a + b = 0} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a = 2} \\ {b = – 4} \\ {c = 3} \end{array}} \right.\)
Nên \(S = {a^2} + {b^2} + {c^2}\)=29
Câu 5:
Parabol \(y = a{x^2} + bx + 2\) đi qua hai điểm \(M(1;5)\) và \(N( – 2;8)\) có phương trình là
\(y = 2{x^2} + x + 2\).
Parabol \(y = a{x^2} + bx + 2\) đi qua hai điểm \(M(1;5)\)và \(N( – 2;8)\) nên ta có hệ phương trình:\(\left\{ \begin{gathered} 5 = a{.1^2} + b.1 + 2 \hfill \\ 8 = a.{( – 2)^2} + b.( – 2) + 2 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} a + b = 3 \hfill \\ 4a – 2b = 6 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} a = 1 \hfill \\ b = 2 \hfill \\ \end{gathered} \right.\)
Vậy hàm số cần tìm là \(y = 2{x^2} + x + 2.\)
Vậy hàm số cần tìm là \(y = 2{x^2} + x + 2.\)
Câu 6:
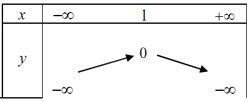
Bảng biến thiên của hàm số \(y = – {x^2} + 2x – 1\) là:
<img src="https://tailieuhoctap.sachtruyen.com.vn/anh-dap-an-trac-nghiem/de-15-phut-bai-16-ham-so-bac-hai-online-co-loi-giai-de-4-5-0-0.jpg" alt="Đề 15 Phút Bài 16 Hàm Số Bậc Hai Online Có Lời Giải-Đề 4" class="mx-auto my-5 rounded-lg shadow-sm max-w-full h-auto" style="max-height: 350px;">
\(y = – {x^2} + 2x – 1\)Có \(a = – 1 < 0\), nên loại C và D
Tọa độ đỉnh \(I\left( {1;0} \right)\), nên nhận A
Tọa độ đỉnh \(I\left( {1;0} \right)\), nên nhận A
Câu 7:
Đồ thị hàm số \(y = a{x^2} + bx + c\), \((a \ne 0)\) có hệ số \(a\) là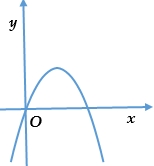

\(a < 0.\)
Bề lõm hướng xuống \(a < 0.\)
Câu 8:
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng?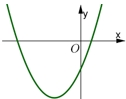

\(a > 0;{\text{ }}b > 0;{\text{ }}c < 0\).
Vì Parabol hướng bề lõm lên trên nên \(a > 0\).
Đồ thị hàm số cắt \(Oy\) tại điểm \(\left( {0;c} \right)\) ở dưới \(Ox \Rightarrow c < 0\).
Hoành độ đỉnh Parabol là \( - \frac{b}{{2a}} < 0\), mà \(a > 0 \Rightarrow b > 0\).
Đồ thị hàm số cắt \(Oy\) tại điểm \(\left( {0;c} \right)\) ở dưới \(Ox \Rightarrow c < 0\).
Hoành độ đỉnh Parabol là \( - \frac{b}{{2a}} < 0\), mà \(a > 0 \Rightarrow b > 0\).
Câu 9:
Giá trị nhỏ nhất của hàm số \(y = 2{x^2} + x – 3\) là
\(\frac{{ - 25}}{8}\).
\(y = 2{x^2} + x – 3 = 2(x + \frac{1}{4}) – \frac{{25}}{8} \geqslant \frac{{ – 25}}{8}\)\(y = \frac{{ – 25}}{8}\,khi\,x = \frac{{ – 1}}{4}\) nên giá trị nhỏ nhất của hàm số \(y = 2{x^2} + x – 3\) là \(\frac{{ – 25}}{8}\).
Câu 10:
Một của hàng buôn giày nhập một đôi với giá là \(40\) đôla. Cửa hàng ước tính rằng nếu đôi giày được bán với giá \(x\) đôla thì mỗi tháng khách hàng sẽ mua \((120 – x)\) đôi. Hỏi của hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?
\(80\) USD
Gọi \(y\) là số tiền lãi của cửa hàng bán giày.
Ta có : \(y = (120 – x)(x – 40) = – {x^2} + 160x – 4800 = – {(x – 80)^2} + 1600 \leqslant 1600\).Dấu “\( = \)” xảy ra \(x = 80\).
Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá \(80\) USD.
Ta có : \(y = (120 – x)(x – 40) = – {x^2} + 160x – 4800 = – {(x – 80)^2} + 1600 \leqslant 1600\).Dấu “\( = \)” xảy ra \(x = 80\).
Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá \(80\) USD.
Giải thích & Đáp án chi tiết
Câu 1
Đáp án đúng: ʍ
\(\left( {2; + \infty } \right)\).
Câu 2
Đáp án đúng: ʌ
\(b \geqslant - 12\).
Câu 3
Đáp án đúng: ʌ
\(x = - \frac{3}{2}\).
Câu 4
Đáp án đúng: ʌ
\(29\).
Câu 5
Đáp án đúng: ʋ
\(y = 2{x^2} + x + 2\).
Câu 6
Đáp án đúng: ʊ
Câu 7
Đáp án đúng: ʋ
\(a < 0.\)
Câu 8
Đáp án đúng: ʍ
\(a > 0;{\text{ }}b > 0;{\text{ }}c < 0\).
Câu 9
Đáp án đúng: ʍ
\(\frac{{ - 25}}{8}\).
Câu 10
Đáp án đúng: ʊ
\(80\) USD
