Trắc nghiệm online đề kiểm tra 1 tiết chương 3-Nguyên hàm, tích phân, ứng dụng (Đề 1)

Question 1

Câu 1:

Nếu \(\int f (x){\rm{ d}}x = {e^x} + \sin x + C\) thì \(f(x)\) bằng

A
\({e^x} + c{\rm{os}}x.\)
B
\({e^x} - \cos x.\)
C
\({e^x} - \sin x.\)
D
\({e^x} + \sin x.\)

Answer

\({e^x} + \sin x.\)

Question 2

Câu 2:

Tích phân \(I = \int\limits_0^{\frac{\pi }{2}} {{{\left( {1 – c{\rm{osx}}} \right)}^n}\sin {\rm{x}}dx} \) có giá trị bằng:

A
\(\frac{1}{n}.\)
B
\( - \frac{1}{{n + 1}}.\)
C
\(\frac{1}{{n + 1}}.\)
D
1

Answer

\( - \frac{1}{{n + 1}}.\)

Question 3

Câu 3:

Diện tích hình phẳng giới hạn đường cong \(y = \frac{{2x – 1}}{{x + 1}}\) ; \(y = 0\) và \(x = 0;x = 1\) là

A
\(2 - 3\ln 2.\)
B
\(3\ln 2 - 2.\)
C
\(3\ln \frac{9}{8}.\)
D
\(2 + \ln 2.\)

Answer

\(3\ln 2 - 2.\)

Question 4

Câu 4:

Trong các mệnh đề sau, mệnh đề nào SAI?

A
\(\int {2f\left( x \right)} dx\, = 2\int {f\left( x \right)} dx.\)
B
\(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx\,\, = \int {f\left( x \right)} dx - \int {g\left( x \right)} dx.\)
C
\(\int {\left[ {f\left( x \right).g\left( x \right)} \right]} dx\,\, = \int {f\left( x \right)} dx.\int {g\left( x \right)dx} .\)
D
\(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx\,\, = \int {f\left( x \right)} dx + \int {g\left( x \right)} dx.\)

Answer

\(\int {\left[ {f\left( x \right).g\left( x \right)} \right]} dx\,\, = \int {f\left( x \right)} dx.\int {g\left( x \right)dx} .\)

Question 5

Câu 5:

Nếu \(f(1) = 12,f'(x)\) liên tục và \(\int\limits_1^4 {f'(x)dx = 17} \), giá trị của f(4) bằng:

A
9
B
19
C
5
D
29

Answer

\(\ln \frac{7}{5}\).

Answer

\(x\sin x + \cos x + C.\)

Answer

\(S = \int\limits_0^1 {\frac{1}{3}{x^3}dx} .\)

Answer

\(\frac{{61\pi }}{{35}}.\)

Answer

Bước 3.

Answer

\(\frac{{128}}{{15}}.\)

Answer

\(\frac{5}{3}\).

Answer

\(V = \pi \int\limits_0^2 {{x^3}} dx.\)

Answer

\(\ln 2 + 1.\)

Answer

\(\,\,\frac{{{7^x}}}{{\ln 7}} + C.\)

Answer

Bước 3.

Answer

\(S = \int\limits_a^b {[g\left( x \right) - f(x)]dx} .\)

Answer

\(4 - 6\ln 2\).

Answer

\(\int\limits_1^2 {{e^t}} dt.\)

Answer

\(\frac{1}{4}\left( {{e^2} + 1} \right)\).

Answer

\(\frac{{{x^3}}}{3} + 3\ln \left| x \right| + \frac{4}{3}\sqrt {{x^3}} + C\)

Answer

\(\int\limits_0^{\frac{\pi }{2}} {{t^4}} dt\).

Answer

\(\frac{1}{2}\).

Question 6

Câu 6:

Giá trị của \(\int\limits_{ – 1}^5 {\frac{1}{{x + 2}}} dx\) bằng

A
0
B
\(\ln \frac{7}{5}\).
C
-ln7
D
ln7

Question 7

Câu 7:

Nguyên hàm của hàm số \(f(x) = x\cos x\) là:

A
\(x\sin x + \cos x + C.\)
B
\(\frac{{{x^2}}}{2}.sinx + C.\)
C
\(x\sin x - \cos x + C.\)
D
\( - \,\frac{{{x^2}}}{2}.sinx + C.\)

Question 8

Câu 8:

Diện tích của phần hình phẳng gạch chéo (H.1) được tính theo công thức: Trắc nghiệm online đề kiểm tra 1 tiết chương 3-Nguyên hàm, tích phân, ứng dụng (Đề 1)

A
\(S = \int\limits_0^1 {{x^2}dx} .\)
B
\(S = \int\limits_0^1 {\frac{1}{3}{x^3}dx} .\)
C
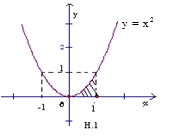
\(S = \int\limits_0^1 {\frac{1}{3}{x^2}dx} .\)
D
\(S = \int\limits_0^1 {2xdx} .\)

Question 9

Câu 9:

Thể tích khối tròn xoay khi quay hình phẳng (H) xác định bởi các đường \(y = \frac{1}{3}{x^3} – {x^2},y = 0,x = 0,x = 3\) quanh trục Ox là:

A
\(\frac{{61\pi }}{{35}}.\)
B
\(\frac{{51\pi }}{{35}}.\)
C
\(\frac{{71\pi }}{{35}}.\)
D
\(\frac{{81\pi }}{{35}}.\)

Question 10

Câu 10:

Một học sinh giải bài toán tính \(\int_1^e {\ln xdx} \) như sau:

Bước 1: Chọn \(\left\{ \begin{array}{l}

u = \ln x\\

dv = dx

\end{array} \right. \Rightarrow \left\{ \begin{array}{l}

du = \frac{1}{x}dx\\

v = x

\end{array} \right.\)

Bước 2: \(I = \left. {x.\ln x} \right|_1^e – \int_1^2 {\frac{1}{x}.xdx} \)

Bước 3: \(I = \left. {e – \frac{{{x^2}}}{2}.\ln \left| x \right|} \right|_1^e\)

Bước 4: \(I = e – \frac{{{e^2}}}{2}\)

Trong các cách giải trên, sai từ bước nào?

A
Bước 1.
B
Bước 2.
C
Bước 3.
D
Bước 4.

Question 11

Câu 11:

Thể tích vật thể tròn xoay của hình giới hạn bởi các đường: \(y = {x^2}\); y = 4; x = 0; x = 2; khi quay quanh trục Ox được tính bởi công thức:

A
\(\frac{{128}}{{15}}.\)
B
\(\frac{{16\pi }}{{13}}.\)
C
\(\frac{{256\pi }}{{15}}.\)
D
\(\frac{{128\pi }}{5}.\)

Question 12

Câu 12:

Tính tích phân sau:\(\int_0^{\frac{\pi }{2}} {(2x – 1)\cos xdx} = m\pi + n\) giá trị của m+n là:

A
-2
B
5
C
2
D
-1

Question 13

Câu 13:

Tích phân\(\int_0^3 {\frac{x}{{1 + \sqrt {1 + x} }}} dx\) có giá trị bằng

A
\(\frac{5}{3}\).
B
\( - \frac{5}{3}\).
C
\(\frac{{19}}{6}\).
D
\( - \frac{{19}}{6}\).

Question 14

Câu 14:

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = {x^3},\,\,y = 0,\,\,x = 2\) quanh trục Ox:

A
\(V = \int\limits_0^2 {{{\left( {\pi {x^3}} \right)}^2}} dx.\)
B
\(V = \pi \int\limits_0^2 {{x^3}} dx.\)
C
\(V = \pi \int\limits_0^2 {{x^6}} dx.\)
D
\(V = \int\limits_0^2 {{x^6}} dx.\)

Question 15

Câu 15:

Biết F(x) là nguyên hàm của hàm số \(y = \frac{1}{{x – 1}}\) và F(2) = 1. Khi đó F(3) bằng bao nhiêu:

A
\(\ln 2 + 1.\)
B
\(\ln \frac{3}{2}.\)
C
\(\ln 2.\)
D
\(\frac{1}{2}.\)

Question 16

Câu 16:

Nguyên hàm của hàm số \(f(x) = {7^x}\) là:

A
\(\,\,\frac{{{7^x}}}{{\ln 7}} + C.\)
B
\(\,{7^x}\ln 7 + C.\)
C
\({7^x} + C.\)
D
\(\frac{{{7^x}}}{{\ln 7}}.\)

Question 17

Câu 17:

Một học sinh giải bài toán tính \(I = \int\limits_0^{\frac{\pi }{4}} {\frac{{2.{e^{{\mathop{\rm tanx}\nolimits} }}dx}}{{{{\cos }^2}x}}} \) như sau:

Bước 1: Đặt \(t = ta{\rm{nx}} \Rightarrow {\rm{dt = }}\frac{1}{{{{\cos }^2}x}}dx\) Bước 2: Đổi cận: \(x = 0 \Rightarrow t = 0;x = \frac{\pi }{4} \Rightarrow t = 1\)

Bước 3: \(I = \int_0^1 {{e^t}dt} = \left. {{e^t}} \right|_0^1\) Bước 4: \(I = e – 1\)

Trong các cách giải trên, sai từ bước nào?

A
Bước 2.
B
Bước 1.
C
Bước 3.
D
Bước 4.

Question 18

Câu 18:

Cho \(f\left( x \right)\) liên tục trên [0; 10] thỏa mãn: \(\int\limits_0^{10} {f\left( x \right)} dx = 7\) , \(\int\limits_6^{10} {f\left( x \right)} dx = 3\). Khi đó, \(\int\limits_0^6 {f\left( x \right)dx} \) có giá trị là:

A
4
B
\(\frac{7}{3}\).
C
21
D
10

Question 19

Câu 19:

Cho hai hàm số \(y = f(x),\,y = g(x)\) liên tục trên [a;b]. Hình phẳng giới hạn bởi đồ thị 2 hàm số \(y = f(x),\,y = g(x)\) và đường thẳng \(x{\rm{ }} = {\rm{ }}a,{\rm{ }}x{\rm{ }} = {\rm{ }}b\) có diện tích S đươc tính bởi công thức

A
\(S = \left| {\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|.\)
B
\(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|} dx.\)
C
\(S = \int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} .\)
D
\(S = \int\limits_a^b {[g\left( x \right) - f(x)]dx} .\)

Question 20

Câu 20:

Diện tích hình phẳng giới hạn bởi các đường cong \(y = {2^x}\),\(y = 2,\,\,x = 3\) là:

A
\(\frac{6}{{\ln 2}} - 4\).
B
\(6\ln 2 - 4\).
C
\(4 - \frac{6}{{\ln 2}}\).
D
\(4 - 6\ln 2\).

Question 21

Câu 21:

Với t = \(\sqrt x \), tích phân \(\int\limits_1^4 {{e^{\sqrt {\rm{x}} }}} dx\) bằng tích phân nào sau đây?

A
\(2\int\limits_1^2 {{e^t}} dt.\)
B
\(\int\limits_1^2 {{e^t}} dt.\)
C
2\(\int\limits_1^2 {t.{e^t}} dt.\)
D
\(\int\limits_1^2 {t.{e^t}} dt.\)

Question 22

Câu 22:

Giá trị của \(\int_0^1 {x.{e^{2x}}} dx\) bằng

A
1
B
\(\frac{1}{4}\left( {{e^2} + 1} \right)\).
C
\(\frac{1}{4}\left( {{e^2} - 1} \right)\).
D
-1

Question 23

Câu 23:

Nguyên hàm của hàm số \(f(x) = {x^2} + \frac{3}{x} – 2\sqrt x \)là:

A
\(\frac{{{x^3}}}{3} + 3\ln \left| x \right| - \frac{4}{3}\sqrt {{x^3}} + C.\)
B
\(\frac{{{x^3}}}{3} + 3\ln x - \frac{3}{4}\sqrt {{x^3}} + C.\)
C
\(\frac{{{x^3}}}{3} - 3\ln \left| x \right| - \frac{4}{3}\sqrt {{x^3}} + C.\)
D
\(\frac{{{x^3}}}{3} + 3\ln \left| x \right| + \frac{4}{3}\sqrt {{x^3}} + C\)

Question 24

Câu 24:

Cho \(I = \int\limits_0^{\frac{\pi }{2}} {{{\sin }^4}} x.\cos xdx\). Đặt \(t = {\mathop{\rm s}\nolimits} {\rm{inx}}\), ta có I bằng:

A
\(\int\limits_0^{\frac{\pi }{2}} {{t^3}\sqrt {1 - {t^2}} } dt\).
B
\(\int\limits_0^{\mathop 1\limits^{} } {{t^4}} \sqrt {1 - {t^2}} dt\).
C
\(\int\limits_0^{\frac{\pi }{2}} {{t^4}} dt\).
D
\(\int\limits_0^{\mathop 1\limits^{} } {{t^4}} dt\).

Question 25

Câu 25:

Giá trị của \(\int_0^{\frac{\pi }{4}} {\sin 2x} dx\) bằng

A
-1
B
\(\frac{1}{2}\).
C
\( - \frac{1}{2}\).
D
1

Trắc nghiệm online đề kiểm tra 1 tiết chương 3-Nguyên hàm, tích phân, ứng dụng (Đề 1)

Đề Kiểm Tra: Trắc nghiệm online đề kiểm tra 1 tiết chương 3-Nguyên hàm, tích phân, ứng dụng (Đề 1)

Giải thích & Đáp án chi tiết