Đề Trắc Nghiệm Bài 16 Hàm Số Bậc Hai Online Có Đáp Án Và Lời Giải-Đề 2
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-trac-nghiem-bai-16-ham-so-bac-hai-online-co-dap-an-va-loi-giai-de-2
Đề Kiểm Tra: Đề Trắc Nghiệm Bài 16 Hàm Số Bậc Hai Online Có Đáp Án Và Lời Giải-Đề 2
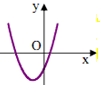
\(\left( { - \infty ;\, - \frac{b}{{2a}}} \right).\)
\((2; + \infty )\)
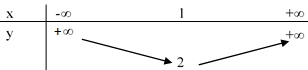
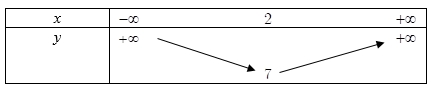 Từ bảng biến thiên ta thấy, hàm số đồng biến trên khoảng\((2; + \infty )\)
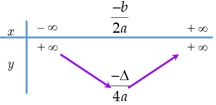
Từ bảng biến thiên ta thấy, hàm số đồng biến trên khoảng\((2; + \infty )\)\(I\left( { - \frac{b}{{2a}};\; - \;\frac{\Delta }{{4a}}} \right)\).
\(1\).
\(2\).
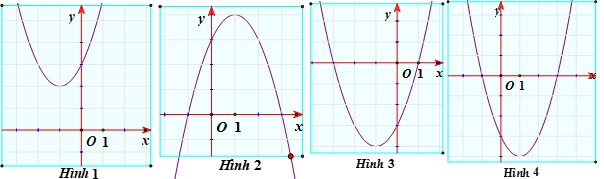
Hình \(4\).
<img src="https://tailieuhoctap.sachtruyen.com.vn/anh-dap-an-trac-nghiem/de-trac-nghiem-bai-16-ham-so-bac-hai-online-co-dap-an-va-loi-giai-de-2-6-2-0.jpg" alt="Đề Trắc Nghiệm Bài 16 Hàm Số Bậc Hai Online Có Đáp Án Và Lời Giải-Đề 2" class="mx-auto my-5 rounded-lg shadow-sm max-w-full h-auto" style="max-height: 350px;">
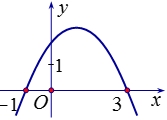 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?\(a < 0\), \(b > 0\), \(c > 0\).
\(y = 2{x^2} - 4x + 4\).
\( - 3\).
Giải thích & Đáp án chi tiết