Đề Thi Thử THPT Quốc Gia Môn Toán Trắc Nghiệm Online-Đề 3
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-thpt-quoc-gia-mon-toan-trac-nghiem-online-de-3
Đề Kiểm Tra: Đề Thi Thử THPT Quốc Gia Môn Toán Trắc Nghiệm Online-Đề 3
720
Một hàm số là một dãy số.
\({S_{\Delta OAB}} = 2.\)
\(I = \frac{3}{4}.\)
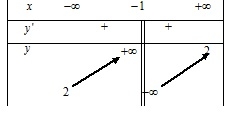
\(y = \frac{{2x - 1}}{{x + 1}}.\)
Nếu hai mặt phẳng phân biệt \(\left( \alpha \right)\)và \(\left( \beta \right)\) song song với nhau thì mọi đường thẳng nằm trong \(\left( \alpha \right)\) đều song song với \(\left( \beta \right)\).
\(D = R\backslash \left\{ {\frac{{k\pi }}{2}|k \in Z} \right\}.\)
Phép đối xứng tâm B.
y = 1
\(2x + y + 3 = 0.\)
Đồ thị hàm số đồng biến trên \(\left( { - \infty ; - \sqrt 3 } \right)\)và \(\left( {0;\sqrt 3 } \right).\)
\(m > 1.\)
Đồ thị hàm số có hai tiệm cận ngang.
\(\frac{\pi }{4}.\)
5 mặt phẳng.
2280.
\(AK \bot BD.\)
\(\frac{{55}}{9}.\)
9 lần.
\(C_{n + 1}^k = C_n^k + C_n^{k - 1}\) (với\(\left( {1 \le k \le n} \right)\)).
Khối chóp tứ giác S.ABCD được phân chia thành hai khối tứ diện C.SAB và C.SAD.
(I): Phép tịnh tiến. (II): Phép đối xứng trục
(III): Phép vị tự với tỉ số \( – 1\). (IV): Phép quay với góc quay \(90^\circ \).
4.
\({y_{\min }} = - 16.\)
26
2.
(C) cắt trục Ox tại 3 điểm phân biệt.
\(x = \pm \frac{\pi }{6} + k\pi ,\left( {k \in \mathbb{Z}} \right).\)
6.
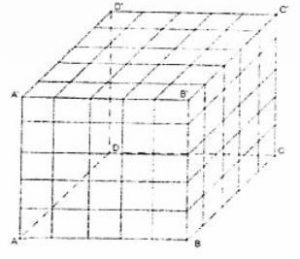
\(a = 4.\)
\(\frac{1}{2}.\)
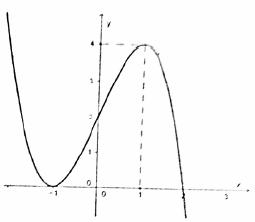
\(y = {\left( {x + 1} \right)^2}\left( {2 - x} \right).\)
\(D\left( { - 4;10} \right)\)
Số chẵn.
1.
2.
\(h = \frac{{a\sqrt 6 }}{2}.\)
4 điểm.
6.
3 tiếp tuyến.
Ba khối chóp
\(y = \sin 2x.\)
Mỗi cạnh của một đa giác của (H) là cạnh chung của nhiều hơn hai đa giác.
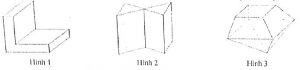
Hình 3 là khối đa diện lồi, hình 1 không phải là khối đa diện lồi.
(I): \(f\left( x \right)\)đạt cực trị tại \({x_0}\)thì \(f’\left( {{x_0}} \right) = 0.\)
(II):\(f\left( x \right)\)có cực đại, cực tiểu thì giá trị cực đại luôn lớn hơn giá trị cực tiểu.
(III):\(f\left( x \right)\)có cực đại thì có cực tiểu.
(IV):\(f\left( x \right)\)đạt cực trị tại \({x_0}\)thì \(f\left( x \right)\)xác định tại \({x_0}\).
1.
\(\left\{ {3;4} \right\}.\)
\(m = 3.\)
\(S = \left( { - \infty ;0} \right) \cup \left[ {\frac{{2 + \sqrt 2 }}{2}; + \infty } \right)\)
\(\frac{5}{8}.\)
Nếu \(\left( {{u_n}} \right)\) là cấp số cộng với công sai khác không thì \(\left( {{S_n}} \right)\) cũng là cấp số cộng.
\({S_{\min }} = 3\sqrt 3 .\)
