Đề Thi Thử THPT Quốc Gia Môn Toán Trắc Nghiệm Online – Đề 4
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-thpt-quoc-gia-mon-toan-trac-nghiem-online-de-4
Đề Kiểm Tra: Đề Thi Thử THPT Quốc Gia Môn Toán Trắc Nghiệm Online – Đề 4
Hàm số đồng biến trên \(R\)
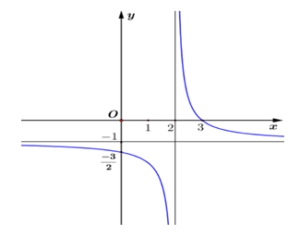
\(y = \frac{{x - 3}}{{x - 2}}\)
\(P = \frac{{\sqrt 3 }}{2}\)
e
\(g\left( x \right) = 1 + 2018\int\limits_0^x {f\left( t \right)} dt,g\left( x \right) = {f^2}\left( x \right).\) Tính \(\int\limits_0^1 {\sqrt {g\left( x \right)} d{\rm{x}}} \)
\(\frac{{1011}}{2}\)
\(\frac{4}{3}\)
\(\frac{6}{{11}}\)
\(a < 0,b < 0,c < 0,d < 0\)
\(\frac{{2\sqrt 5 }}{5}\)
\(2x + 9y - 2\ln 2 - 3 = 0\)
\(\frac{4}{5}\)
\(bc = 2\left( {b + c} \right)\)
\(\frac{7}{{12}}\)
0,016
5i
\(V' = \frac{9}{{16}}{a^3}\)
\(\frac{{\sqrt 2 }}{5}\)
5
1
\({x^2} + {y^2} + {\left( {z + 2} \right)^2} = 25\)
\( - \frac{9}{4}\).
9
\(a + 2b = 7\)
\(12x + 15y + 20z + 60 = 0\)
\(\frac{{105}}{2}\pi \)
I. Hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {3; + \infty } \right)\)
II. Hàm số \(y = g\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty ; – 3} \right)\)
III. Hàm số \(y = g\left( x \right)\)có 5 điểm cực trị
IV. \(\mathop {Min}\limits_{x \in R} g\left( x \right) = f\left( 9 \right)\)
Số phát biểu đúng là
1
\( + \infty \)
\(G\left( {2;2;4} \right)\)
\(\frac{{x - 3}}{3} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 5}}{5}\)
\(F\left( x \right) = 3{\rm{x}} + \tan x + C\)
\(V = \frac{{8\pi }}{3}\)
\(\frac{1}{3}\ln \frac{4}{5} + \ln 2 + 1\)
3a
3
84
\(\frac{{\pi {a^2}}}{2}\)
2017
\(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = \frac{{13}}{{27}}\)
\(S = \int\limits_a^b {\left| {f\left( x \right)} \right|} d{\rm{x}}\)
\(S = \left( { - \infty ;1} \right)\)
9.
45
\(\overrightarrow n = \left( {2;4; - 3} \right)\)
\(Q\left( {2;1;0} \right)\)
\(x = 1\)
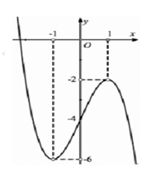
1
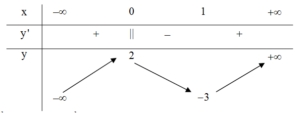
Trong các khẳng định sau, khẳng định nào đúng?
Hàm số có giá trị cực tiểu bằng 1
10
\(V = 4\pi {R^2}\)
\(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\)
