Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Question 1

Câu 1:

Biết \(\int\limits_0^1 {f\left( x \right)dx} = – 2\) và \(\int\limits_0^1 {g\left( x \right)dx} = 3,\) khi đó \(\int\limits_0^1 {\left[ {f\left( x \right) – g\left( x \right)} \right]dx} \) bằng

A
\( - 5.\)
B
1.
C
5.
D
\( - 1.\)

Answer

\({M_3}\left( { - \frac{1}{4};1} \right)\).

Answer

\(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} .\)

Answer

\(x = 2.\)

Answer

\(\frac{{14}}{{27}}\)

Answer

\(2{x^2} + 5x + C.\)

Answer

\( - 3 + 4i.\)

Answer

\(a\frac{{\sqrt 3 }}{7}\).

Answer

\(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^5 {f\left( x \right)dx} \)

Answer

\(\left( {\frac{2}{5};\frac{3}{7}} \right).\)

Answer

\(\left( {0;2} \right).\)

Answer

\(90^\circ .\)

Answer

\(\frac{{\sqrt {21} a}}{{14}}.\)

Answer

\(y = {x^3} - 3{x^2} + 3.\)

Answer

\(\frac{1}{2}lo{g_5}a.\)

Answer

\(x = 1.\)

Answer

\(\left\{ \begin{array}{l} x = 1 + t\\ y = 4\\ z = 2 + 2t \end{array} \right.\)

Answer

\(\left[ {2; + \infty } \right).\)

Answer

\(\sqrt 5 .\)

Answer

\(\frac{{x - 1}}{2} = \frac{y}{3} = \frac{{z + 2}}{1}.\)

Answer

\(12\sqrt 3 \)

Answer

\(16\sqrt 2 \pi \)

Answer

\(\frac{{{a^3}}}{4}.\)

Answer

\(\left( { - 3;\,\,3} \right)\)

Answer

\(x + y + 2z - 3 = 0.\)

Answer

\(\left\{ \begin{array}{l} x = - 1 + 2t\\ y = 2t\\ z = 3t \end{array} \right..\)

Answer

\(\left( {0;0; - 1} \right).\)

Answer

\({7^2}.\)

Answer

\(M\left( {0; - 3; - 5} \right).\)

Answer

\(3\ln \left( {x - 1} \right) + \frac{2}{{x - 1}} + C\)

Answer

\(\overrightarrow {{u_4}} = \left( {1;2; - 3} \right).\)

Answer

\(m \ge f\left( 0 \right).\)

Answer

\(S = 17.\)

Answer

\(\left( {{x^2} - 3x} \right){2^{{x^2} - 3x + 1}}.\)

Answer

\(MN = 2\sqrt 5 \).

Answer

\(\frac{1}{3}\pi {r^2}h.\)

Question 2

Câu 2:

Kí hiệu \({z_0}\) là nghiệm phức có phần ảo dương của phương trình \(4{z^2} – 16z + 17 = 0\). Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức \(w = i{z_0}\)?

A
\({M_4}\left( {\frac{1}{4};1} \right)\).
B
\({M_3}\left( { - \frac{1}{4};1} \right)\).
C
\({M_2}\left( { - \frac{1}{2};2} \right)\).
D
\({M_1}\left( {\frac{1}{2};2} \right)\).

Question 3

Câu 3:

Cho hàm số \(f\left( x \right)\) liên tục trên Gọi S là diện tích hình phẳng giới hạn bởi các đường\(y = f\left( x \right),\)\(y = 0,x = – 1\) và \(x = 4\) (như hình vẽ bên).

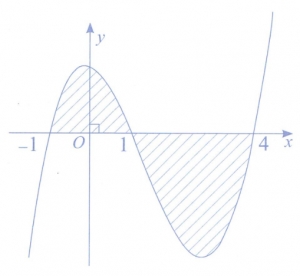
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Mệnh đề nào dưới đây đúng?

A
\(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} .\)
B
\(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} .\)
C
\(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} .\)
D
\(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} .\)

Question 4

Câu 4:

Cho hàm số \(y = f\left( x \right),\) bảng biến thiên của hàm số \(f’\left( x \right)\) như sau

Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Số điểm cực trị của hàm số \(y = f\left( {{x^2} + 2x} \right)\) là

A
5.
B
9.
C
3.
D
7.

Question 5

Câu 5:

Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

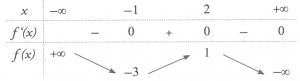
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Hàm số đã cho đạt cực tiểu tại

A
\(x = - 1.\)
B
\(x = - 3.\)
C
\(x = 2.\)
D
\(x = 1.\)

Question 6

Câu 6:

Chọn ngẫu nhiên hai số khác nhau từ 27 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng

A
\(\frac{{14}}{{27}}\)
B
\(\frac{1}{2}\)
C
\(\frac{{365}}{{729}}\)
D
\(\frac{{13}}{{27}}\)

Question 7

Câu 7:

Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 2x – 2z – 7 = 0.\) Bán kính của mặt cầu đã cho bằng

A
\(\sqrt 7 .\)
B
\(\sqrt {15} .\)
C
9.
D
3.

Question 8

Câu 8:

Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = 2x + 5\) là

A
\(2{x^2} + 5x + C.\)
B
\({x^2} + 5x + C.\)
C
\(2{x^2} + C.\)
D
\({x^2} + C.\)

Question 9

Câu 9:

Số phức liên hợp của số phức \(3 – 4i\) là

A
\( - 4 + 3i.\)
B
\(3 + 4i.\)
C
\( - 3 + 4i.\)
D
\( - 3 - 4i.\)

Question 10

Câu 10:

Cho lăng trụ đứng \(ABC.A’B’C’\) có \(AC = a;BC = 2a,\angle ACB = 120^\circ \). Gọi M là trung điểm của \(BB’\). Tính khoảng cách giữa hai đường thẳng AM và \(CC’\) theo a.

A
\(a\frac{{\sqrt 7 }}{7}\).
B
\(a\frac{{\sqrt 3 }}{7}\).
C
\(a\sqrt {\frac{3}{7}} \).
D
\(a\sqrt 3 \).

Question 11

Câu 11:

Cho a và b là hai số thực dương thỏa mãn \({a^4}b = 16.\) Giá trị của \(4{log _2}a + {log _2}b\) bằng

A
8.
B
16.
C
2.
D
4.

Question 12

Câu 12:

Cho phương trình \({log _9}{x^2} – {log _3}left( {6x – 1}ight) = – {log _3}m\) (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm?

A
6
B
5
C
7
D
Vô số

Question 13

Câu 13:

Cho hàm số \(y = f\left( x \right)\) liên tục trên . Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),\,\,y = 0,\,\,x = – 1\) và \(x = 5\) (như hình vẽ).

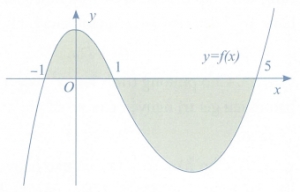
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Mệnh đề nào sau đây đúng?

A
\(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^5 {f\left( x \right)dx} \)
B
\(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^5 {f\left( x \right)dx} \)
C
\(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^5 {f\left( x \right)dx} \)
D
\(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^5 {f\left( x \right)dx} \)

Question 14

Câu 14:

Cho hàm số \(y = f\left( x \right),\) bảng biến thiên của hàm số \(f’\left( x \right)\) như sau:

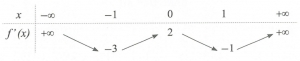
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Số điểm cực trị của hàm số \(y = f\left( {{x^2} – 2x} \right)\) là

A
5.
B
7.
C
3.
D
9.

Question 15

Câu 15:

Cho đường thẳng \(y = x\) và parabol \(y = \frac{1}{2}{x^2} + a\) (a là tham số thực dương). Gọi \({S_1}\) và \({S_2}\) lần lượt là diện tích của hai hình phẳng được bôi đậm trong hình vẽ dưới đây.

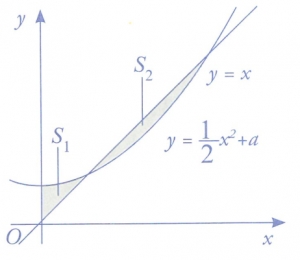
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Khi \({S_1} = {S_2}\) thì a thuộc khoảng nào dưới đây?

A
\(\left( {\frac{1}{3};\frac{2}{5}} \right).\)
B
\(\left( {\frac{3}{7};\frac{1}{2}} \right).\)
C
\(\left( {\frac{2}{5};\frac{3}{7}} \right).\)
D
\(\left( {0;\frac{1}{3}} \right).\)

Question 16

Câu 16:

Cho hàm số có bảng biến thiên như sau:

Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A
\(\left( { - 2;0} \right).\)
B
\(\left( {2; + \infty } \right).\)
C
\(\left( {0;2} \right).\)
D
\(\left( {0; + \infty } \right).\)

Question 17

Câu 17:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng \(\left( {ABC} \right),\)\(SA = 2a,\) tam giác ABC vuông tại B, \(AB = a\sqrt 3 \) và \(BC = a\).

Góc giữa đường thẳng SC và mặt phẳng \(\left( {ABC} \right)\) bằng

A
\(60^\circ .\)
B
\(90^\circ .\)
C
\(30^\circ .\)
D
\(45^\circ .\)

Question 18

Câu 18:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và

nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ A đến mặt phẳng \(\left( {SBD} \right)\) bằng

A
\(\frac{{\sqrt {21} a}}{{28}}.\)
B
\(\frac{{\sqrt {21} a}}{{14}}.\)
C
\(\frac{{\sqrt {21} a}}{7}.\)
D
\(\frac{{\sqrt 2 a}}{2}.\)

Question 19

Câu 19:

Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} – 3x + 2\) trên đoạn \(\left[ { – 3;3} \right]\) là

A
0.
B
4.
C
20.
D
\( - 16.\)

Question 20

Câu 20:

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

A
\(y = {x^3} - 3{x^2} + 3.\)
B
\(y = - {x^3} + 3{x^2} + 3.\)
C
\(y = - {x^4} + 2{x^3} + 3.\)
D
\(y = {x^4} - 2{x^3} + 3.\)

Question 21

Câu 21:

Cho phương trình \(lo{g_9}{x^2} – {\log _3}\left( {3x – 1} \right) = – {\log _3}m\) (m là số thực). Có tất cả bao nhiêu giá trị nguyên của tham số m để phuong trình đã cho có nghiệm?

A
Vô số.
B
3.
C
4.
D
2.

Question 22

Câu 22:

Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 3\) và \({u_2} = 9.\) Công sai của cấp số cộng đã cho bằng

A
12.
B
6.
C
3.
D
\( - 6.\)

Question 23

Câu 23:

Với a là số thực dương tùy ý, \(lo{g_5}{a^2}\) bằng

A
\(\frac{1}{2}lo{g_5}a.\)
B
\(\frac{1}{2} + lo{g_5}a.\)
C
\(2 + lo{g_5}a.\)
D
\(2lo{g_5}a.\)

Question 24

Câu 24:

Nghiệm của phương trình: \({3^{2x – 1}} = 27\) là

A
\(x = 5.\)
B
\(x = 4.\)
C
\(x = 1.\)
D
\(x = 2.\)

Question 25

Câu 25:

Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.

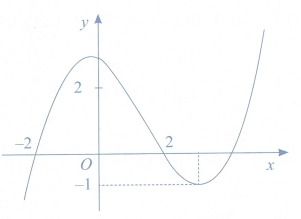
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Số nghiệm thực của phương trình \(\left| {f\left( {{x^3} – 3x} \right)} \right| = \frac{1}{2}\) là

A
6
B
12
C
10
D
3

Question 26

Câu 26:

Trong không gian Oxyz, cho các điểm \(A\left( {1;\,\,0;\,2} \right),\,\,B\left( {1;\,2;\,1} \right),\,\,C\left( {3;\,\,2;\,\,0} \right)\) và \(D\left( {1;\,\,1;\,\,3} \right)\). Đường thẳng đi qua A và vuông góc với mặt phẳng (BCD) có phương trình là

A
\(\left\{ \begin{array}{l}

x = 1 - t\\

y = 2 - 4t\\

z = 2 - 2t

\end{array} \right.\)
B
\(\left\{ \begin{array}{l}

x = 1 - t\\

y = 4t\\

z = 2 + 2t

\end{array} \right.\)
C
\(\left\{ \begin{array}{l}

x = 1 + t\\

y = 4\\

z = 2 + 2t

\end{array} \right.\)
D
\(\left\{ \begin{array}{l}

x = 2 + t\\

y = 4 + 4t\\

z = 4 + 2t

\end{array} \right.\)

Question 27

Câu 27:

Cho hai hàm số \(y = \frac{{x – 3}}{{x – 2}} + \frac{{x – 2}}{{x – 1}} + \frac{{x – 1}}{x} + \frac{x}{{x + 1}}\) và \(y = \left| {x + 2} \right| – x + m\) (m là tham số thực) có đồ thị lần lượt là \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\) Tập hợp tất cả các giá trị của m để \(\left( {{C_1}} \right)\)và \(\left( {{C_2}} \right)\) cắt nhau tại đúng bốn điểm phân biệt là

A
\(\left( { - \infty ;2} \right].\)
B
\(\left[ {2; + \infty } \right).\)
C
\(\left( { - \infty ;2} \right).\)
D
\(\left( {2; + \infty } \right).\)

Question 28

Câu 28:

Cho số phức z thỏa mãn \(3(\overline z + i) – \left( {2 – i} \right)z = 3 + 10i.\) Môđun của z bằng

A
3.
B
5.
C
\(\sqrt 5 .\)
D
\(\sqrt 3 .\)

Question 29

Câu 29:

Trong không gian với hệ toạ độ \(Oxyz,\) phương trình nào dưới đây là phương trình chính tắc của đường thẳng \(d:\left\{ \begin{array}{l}

x = 1 + 2t\\

y = 3t\\

z = – 2 + t

\end{array} \right.?\)

A
\(\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z - 2}}{1}.\)
B
:)\(\frac{{x - 1}}{1} = \frac{y}{3} = \frac{{z + 2}}{{ - 2}}.\)
C
\(\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z - 2}}{{ - 2}}.\)
D
\(\frac{{x - 1}}{2} = \frac{y}{3} = \frac{{z + 2}}{1}.\)

Question 30

Câu 30:

Cho lăng trụ \(ABC.A’B’C’\) có chiều cao bằng 8 và đáy là tam giác đều cạnh bằng 4. Gọi M, N và P lần lượt là tâm các mặt bên \(ABB’A’,\,\,ACC’A’\) và \(BCC’B’\). Thể tích của khối đa diện lồi có các đỉnh là các điểm A, B, C, M, N, P bằng

A
\(12\sqrt 3 \)
B
\(\frac{{40\sqrt 3 }}{3}\)
C
\(16\sqrt 3 \)
D
\(\frac{{28\sqrt 3 }}{3}\)

Question 31

Câu 31:

Cho hình trụ có chiều cao bằng \(4\sqrt 2 \). Cắt hình trụ đã cho bởi một mặt phẳng song song với trục và cách trục một khoảng bằng \(\sqrt 2 \), thiết diện thu được có diện tích bằng 16. Diện tích xung quanh của hình trụ đã cho bằng

A
\(12\sqrt 2 \pi \)
B
\(8\sqrt 2 \pi \)
C
\(24\sqrt 2 \pi \)
D
\(16\sqrt 2 \pi \)

Question 32

Câu 32:

Cho khối lăng trụ đứng \(ABC.A’B’C’\) có đáy là tam giác đều cạnh a và \(AA’ = \sqrt 3 a\). Thể tích khối lăng trụ đã cho bằng

A
\(\frac{{{a^3}}}{4}.\)
B
\(\frac{{3{a^3}}}{2}.\)
C
\(\frac{{{a^3}}}{2}.\)
D
\(\frac{{3{a^3}}}{4}.\)

Question 33

Câu 33:

Cho hai số phức \({z_1} = – 2 + i\) và \({z_2} = 1 + i\). Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức \(2{z_1} + {z_2}\) có tọa độ là

A
\(\left( {3;\,\, - 3} \right)\)
B
\(\left( {2;\,\, - 3} \right)\)
C
\(\left( { - 3;\,\,3} \right)\)
D
\(\left( { - 3;\,\,2} \right)\)

Question 34

Câu 34:

Trong không gian Oxyz, cho hai điểm \(A\left( {1;3;0} \right)\) và \(B\left( {5;1; – 2} \right).\) Mặt phẳng trung trực của đoạn thẳng AB có phương trình là

A
\(3x + 2y - z - 14 = 0.\)
B
\(x + y + 2z - 3 = 0.\)
C
\(2x - y - z - 5 = 0.\)
D
\(2x - y - z + 5 = 0.\)

Question 35

Câu 35:

Trong không gian Oxyz, cho điểm \(A\left( {1;2;3} \right)\) và đường thẳng \(d:\frac{{x – 3}}{2} = \frac{{y – 1}}{1} = \frac{{z + 7}}{{ – 2}}\). Đường thẳng đi qua A, vuông góc với d và cắt trục Oy có phương trình là

A
\(\left\{ \begin{array}{l}

x = t\\

y = - 2 + 4t\\

z = 3t

\end{array} \right..\)
B
\(\left\{ \begin{array}{l}

x = - 1 + 2t\\

y = 2t\\

z = 3t

\end{array} \right..\)
C
\(\left\{ \begin{array}{l}

x = - 1 + 2t\\

y = - 2t\\

z = t

\end{array} \right..\)
D
\(\left\{ \begin{array}{l}

x = 1 - t\\

y = 2 - 4t\\

z = 3 - 3t

\end{array} \right..\)

Question 36

Câu 36:

Cho hàm số f(x) có bảng biến thiên như sau:

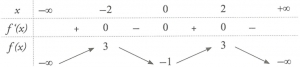
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Số nghiệm thực của phương trình \(2f\left( x \right) – 3 = 0\) là

A
4.
B
1.
C
3.
D
2.

Question 37

Câu 37:

Cho phương trình \(\left( {2\log _2^2x – 3{{\log }_2}x – 2} \right)\sqrt {{3^x} – m} = 0\) (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt?

A
80
B
79
C
Vô số
D
81

Question 38

Câu 38:

Trong không gian Oxyz, hình chiếu vuông góc của điểm \(M\left( {2;1; – 1} \right)\) trên trục Oz có tọa độ là

A
\(\left( {2;1;0} \right).\)
B
\(\left( {0;0; - 1} \right).\)
C
\(\left( {2;0;0} \right).\)
D
\(\left( {0;1;0} \right).\)

Question 39

Câu 39:

Số cách chọn 2 học sinh từ 7 học sinh là

A
\(C_7^2.\)
B
\(A_7^2.\)
C
\({7^2}.\)
D
\({2^7}.\)

Question 40

Câu 40:

Trong không gian Oxyz, cho điểm \(A\left( {0;4; – 3} \right).\) Xét đường thẳng d thay đổi, song song với trục Oz và cách trục Oz một khoảng bằng 3. Khi khoảng cách từ A đến d nhỏ nhất, d đi qua điểm nào dưới đây?

A
\(Q\left( {0;5; - 3} \right).\)
B
\(N\left( {0;3; - 5} \right).\)
C
\(M\left( {0; - 3; - 5} \right).\)
D
\(P\left( { - 3;0; - 3} \right).\)

Question 41

Câu 41:

Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \frac{{3x + 1}}{{{{\left( {x – 1} \right)}^2}}}\) trên khoảng \(\left( {1;\,\, + \infty } \right)\) là

A
\(3\ln \left( {x - 1} \right) + \frac{2}{{x - 1}} + C\)
B
\(3\ln \left( {x - 1} \right) - \frac{1}{{x - 1}} + C\)
C
\(3\ln \left( {x - 1} \right) + \frac{1}{{x - 1}} + C\)
D
\(3\ln \left( {x - 1} \right) - \frac{2}{{x - 1}} + C\)

Question 42

Câu 42:

Thể tích khối lăng trụ có diện tích đáy B và có chiều cao h là

A
\(3Bh.\)
B
\(Bh.\)
C
\(\frac{1}{3}Bh.\)
D
\(\frac{4}{3}Bh.\)

Question 43

Câu 43:

Trong không gian Oxyz, cho đường thẳng \(d:\frac{{x – 2}}{{ – 1}} = \frac{{y – 1}}{2} = \frac{{z + 3}}{1}.\) Vectơ nào dưới đây là một vectơ chỉ phương của d?

A
\(\overrightarrow {{u_1}} = \left( {2;1; - 3} \right).\)
B
\(\overrightarrow {{u_3}} = \left( { - 1;2;1} \right).\)
C
\(\overrightarrow {{u_4}} = \left( {1;2; - 3} \right).\)
D
\(\overrightarrow {{u_2}} = \left( {2;1;1} \right).\)

Question 44

Câu 44:

Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên \(\left[ {0;6} \right]\). Đồ thị của hàm số \(y = f’\left( x \right)\) trên đoạn \(\left[ {0;6} \right]\) được cho bởi hình vẽ bên.

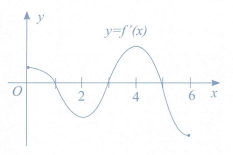
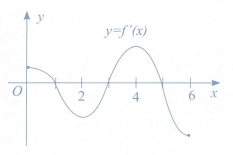
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Hàm số \(y = {\left[ {f\left( x \right)} \right]^2} + 2021\) có tối đa bao nhiêu điểm cực trị

trên đoạn \(y = f’\left( x \right)\)?

A
4.
B
7.
C
3.
D
6.

Question 45

Câu 45:

Cho hàm số \(y = f\left( x \right),\) hàm số \(y = f’\left( x \right)\) liên tục trên và có đồ thị như hình vẽ dưới

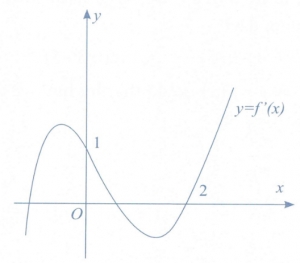
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Bất phương trình \(f\left( x \right) < x + m\) (m là tham số thực) nghiệm đúng với mọi \(x \in \left( {0;2} \right)\) khi và chỉ khi

A
\(m \ge f\left( 2 \right) - 2.\)
B
\(m \ge f\left( 0 \right).\)
C
\(m > f\left( 2 \right) - 2.\)
D
\(m > f\left( 0 \right).\)

Question 46

Câu 46:

Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

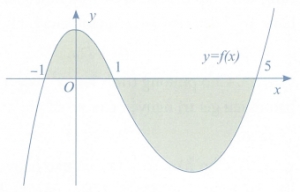
Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Tổng số các đường tiệm cận đứng và tiệm cạn ngang của đồ thị hàm số đã cho là

A
4.
B
2.
C
3.
D
1.

Question 47

Câu 47:

Cho hai số dương x, y thỏa mãn \({\log _2}{\left( {4x + y + 2xy + 2} \right)^{y + 2}} = 8 – \left( {2x – 2} \right)\left( {y + 2} \right)\). Giá trị nhỏ nhất của \(P = 2x + y\) là số có dạng \(M = a\sqrt b + c\) với . Khi đó \(S = a + b + c\) bằng

A
\(S = 3.\)
B
\(S = 7.\)
C
\(S = 19.\)
D
\(S = 17.\)

Question 48

Câu 48:

Hàm số \(y = {2^{{x^2} – 3x}}\) có đạo hàm là

A
\(\left( {{x^2} - 3x} \right){2^{{x^2} - 3x + 1}}.\)
B
\(\left( {2x - 3} \right){2^{{x^2} - 3x}}.\)
C
\({2^{{x^2} - 3x}}\ln 2.\)
D
\(\left( {2x - 3{\rm{ }}} \right){2^{{x^2} - 3x}}.ln2\)

Question 49

Câu 49:

Gọi \({z_1}\) và \({z_2}\)là các nghiệm của phương trình \({z^2} – 4z + 9 = 0\). Gọi \(M,{\rm{ }}N\) là các điểm biểu diễn của \({z_1}\) và \({z_2}\) trên mặt phẳng phức. Khi đó độ dài của \(MN\) là

A
\(MN = - 2\sqrt 5 \).
B
\(MN = 4\).
C
\(MN = 5\).
D
\(MN = 2\sqrt 5 \).

Question 50

Câu 50:

Thể tích của khối nón có chiều cao h và bán kính đáy r là

A
\(\frac{1}{3}\pi {r^2}h.\)
B
\(\pi {r^2}h.\)
C
\(\frac{4}{3}\pi {r^2}h.\)
D
\(2\pi {r^2}h.\)

Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 1)

Giải thích & Đáp án chi tiết