Đề Thi Thử Tốt Nghiệp THPT 2022 Online Môn Toán Bám Sát Đề Tham Khảo-Đề 1
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-thpt-2022-online-mon-toan-bam-sat-de-tham-khao-de-1
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT 2022 Online Môn Toán Bám Sát Đề Tham Khảo-Đề 1
\( - \frac{1}{2}\sin 2x + C\).
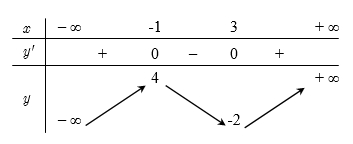
 Số điểm cực của hàm số \(y = f\left( x \right)\) là:
Số điểm cực của hàm số \(y = f\left( x \right)\) là:\(5\).
\(S = \left( {\frac{1}{2};\,5} \right)\).
\(1\).
\(D = \left( {\frac{3}{2}; + \infty } \right)\).
\(x = 3\).
\(29\)
\(36\).
\(\overrightarrow n = \left( { - 2;0; - 3} \right)\).
\(\left( {5; - 1; - 1} \right)\).
\(T\left( {2; - 1} \right)\).
\(y = \frac{1}{2}\).
\(\frac{1}{2}{\log _2}\left( {2a} \right)\).
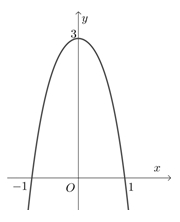
\(y = {x^3} + 3{x^2} - 3\).
\(E\left( {2; - 2;3} \right)\).
\(C_n^k = \frac{{\left( {n + k} \right)!}}{{n!k!}}\).
\(\frac{{{a^3}}}{3}\).
\(y' = \frac{{{{2022}^x}}}{{{\text{ln}}\,2022}}.\)
 Hàm số đã cho đồng biến trong khoảng nào?
Hàm số đã cho đồng biến trong khoảng nào?\(\left( { - 1;0} \right)\).
\(3a\).
\(18.\)
\(4\).
\(\int {{e^x}dx = \frac{1}{{{e^{ - x}}}} + C} \).
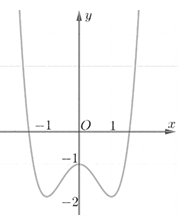
 Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?\(x = - 1\)
\( - 7\).
\(y = {x^3} - 2{{\text{x}}^2} + 6{\text{x}} - 1\).
\(a = {b^3}\).
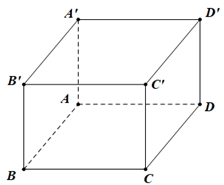
\({90^o}\).
\( - 3\).
Cắt nhau.
\(3.\)
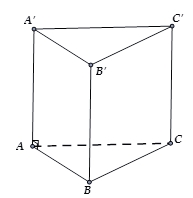 Khoảng cách từ \(C\) đến mặt phẳng \(\left( {ABB'A'} \right)\) bằng
Khoảng cách từ \(C\) đến mặt phẳng \(\left( {ABB'A'} \right)\) bằng\(2\sqrt 3 .\)
\(\frac{{19}}{{40}}\).
\(x - y - 2{\text{z}} - 3 = 0\).
\(18\).
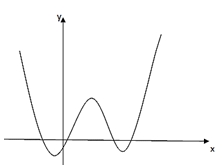 Số giao điểm của đồ thị hàm số \(y = {\left[ {f'\left( x \right)} \right]^2} – f''\left( x \right).f\left( x \right)\) và trục \(Ox\) là:
Số giao điểm của đồ thị hàm số \(y = {\left[ {f'\left( x \right)} \right]^2} – f''\left( x \right).f\left( x \right)\) và trục \(Ox\) là:\(2\).
\(I = 6\).
\(\frac{{{a^3}}}{3}\).
\(4\).
\(2\).
\(\frac{{71}}{6}\).
\(\left\{ \begin{gathered}x = - 3 + 3t \hfill \\y = 5 - 2t \hfill \\z = - 1 + t \hfill \\\end{gathered} \right..\)
\(\frac{{16\sqrt {13} }}{3}\pi {a^2}\).
\(2\).
\(1\).
\(27.\)
\(5\).
\(\left( { - 1;2;3} \right)\)
\(M(1;0)\).
\(\frac{{32\pi }}{3}\).
