Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 2)
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-thpt-2021-online-mon-toan-de-2
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT 2021 Online Môn Toán (Đề 2)
\(h = \frac{{\sqrt 3 a}}{6}\).
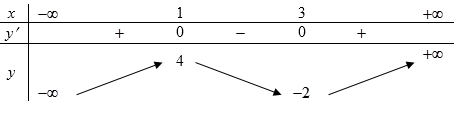 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?Hàm số đạt cực đại tại x = 1 .
\(y = - \frac{1}{3}\).
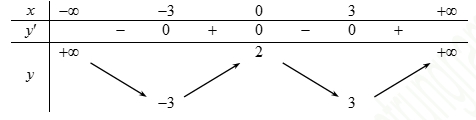 Tìm tất cả giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) – m = 0\) có bốn nghiệm phân biệt.
Tìm tất cả giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) – m = 0\) có bốn nghiệm phân biệt.\(m < - 2\).
\( - 1 + 2i\)
\(3\) triệu 600 ngàn đồng.
\(V = \frac{4}{3}\pi {r^2}h\).
\(y = {\left( {0,7} \right)^x}\).
\(45^\circ \).
12.
\(3\).
\(\frac{{2\sqrt 3 }}{3}{a^3}.\).
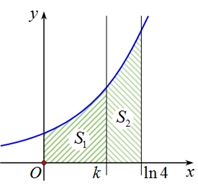 Tìm \(k\) để \({S_1} = 2{S_2}\).
Tìm \(k\) để \({S_1} = 2{S_2}\).\(k = \ln \frac{8}{3}\).
16
\(m \ne 2\).
\(\log _2^2x - {\log _2}x + 6 = 0\)
\(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 3\).
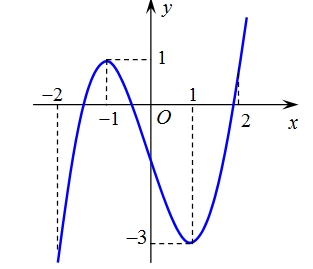 Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?\(\left( { - 2;1} \right)\).
\( - 5i\).
4
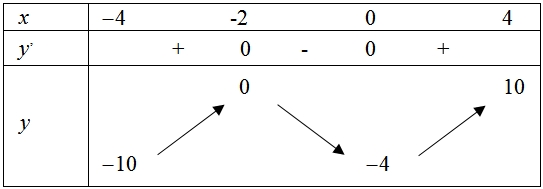 Phát biểu nào sau đây đúng?
Phát biểu nào sau đây đúng?Hàm số không có GTLN, GTNN trên \(( - 4;4)\).
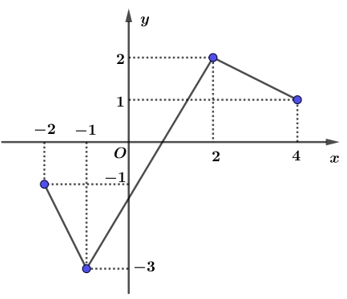 Tìm \(\mathop {\max }\limits_{\left[ { – 2;{\rm{4}}} \right]} \left| {f\left( x \right)} \right|\).
Tìm \(\mathop {\max }\limits_{\left[ { – 2;{\rm{4}}} \right]} \left| {f\left( x \right)} \right|\).\(\left| {f\left( 0 \right)} \right|\).
\({\log _b}x = {\log _b}a.{\log _a}x\).
\(11x + 7y - 2z + 7 = 0\).
\(\frac{{8\pi }}{3}\).
\(\left( { - 2;0} \right)\)
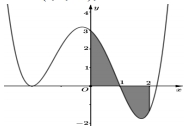 Diện tích của hình phẳng giới hạn bới đồ thị \(\left( C \right)\) và hai đường thẳng \(x = 0\), \(x = 2\)(phần tô đen) là
Diện tích của hình phẳng giới hạn bới đồ thị \(\left( C \right)\) và hai đường thẳng \(x = 0\), \(x = 2\)(phần tô đen) là\(S = \int_0^2 {f\left( x \right){\rm{d}}x} \).
\(F\left( x \right) = - \frac{{\cos 2x}}{2} + {x^2} + C\)
\(5\)
\(x = 6\).
Một đường tròn.
\(\left( { - \infty ; - 3} \right)\)
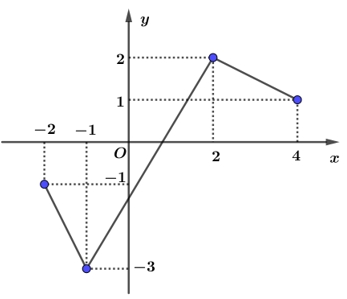 Hỏi hàm số đó là hàm số nào?
Hỏi hàm số đó là hàm số nào?\(y = - {x^3} + 3x.\)
\(\left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = 1 - 2t}\\{z = 2 + 3t}\end{array}} \right.\).
\(\vec c = \left( {8; - 2; - 6} \right)\).
\(\frac{{2a\sqrt 5 }}{5}\).
\(\frac{{{x^n}}}{{{y^n}}} = {\left( {\frac{x}{y}} \right)^n}\)
\(x \ne k2\pi \).
\({a^{\frac{5}{6}}}\).
\(2x + 7y + 4z - - 4 = 0\)
\( - 2\)
\(6\pi \).
\(\frac{{3{a^3}}}{{\sqrt 7 }}\).
34.
\(m \ge 3\)
\(\cos x - x + C\).
\(1\)
\(I\left( {1; - 1;1} \right)\), \(R = 2\).
\(36\pi \).
\(m > - 3\).
