Đề Thi Thử TN 2022 Online Môn Toán Theo Đề Minh Họa-Đề 3
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tn-2022-online-mon-toan-theo-de-minh-hoa-de-3
Đề Kiểm Tra: Đề Thi Thử TN 2022 Online Môn Toán Theo Đề Minh Họa-Đề 3
\(z = \frac{1}{{1 - 3i}}\)
\(\sqrt 6 \)
\(M\left( { - 1;2} \right)\).
\(S = \pi {a^2}.\)
\(2{x^2} - \cos x + C\).
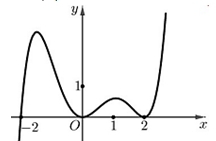
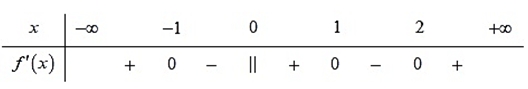 Hàm số đã cho có bao nhiêu điểm cực đại?
Hàm số đã cho có bao nhiêu điểm cực đại?4
\(x \leqslant 7.\)
\(V = abc\).
\(D = \left( { - \infty ;2} \right)\).
\(x = 5\).
\(17\).
\( - 5 + i\).
\(\overrightarrow {{n_1}} = \left( { - 3; - 1; - 1} \right)\)
\(\left( {1;2;3} \right)\).
\(Q\left( {5;1} \right)\)
\(x = 3\)
\(1 - \frac{1}{2}\ln a\)
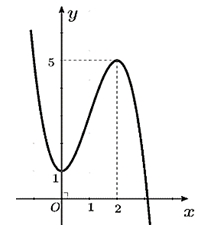
\(y = {x^3} - 3{x^2} + 1\).
\(\overrightarrow {m{\text{ }}} = \left( {1;1;1} \right)\).
\(24\)
\(24\).
\(y' = {13^x}\ln 13\).
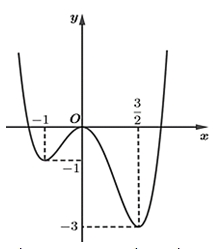
\(\left( {\frac{3}{2}; + \infty } \right)\)
\(6\pi \).
\(12\).
22
\(\int {f\left( x \right){\text{d}}x} = \frac{1}{5}\ln \left( {5x + 4} \right) + C\).
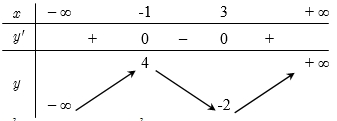 Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?\(x = - 1\)
\(f\left( 3 \right)\).
\(y = {x^4} + {x^2} + 2\).
\({\log _c}a = \frac{2}{3}\).
\(\cos \alpha = \frac{{\sqrt 3 }}{3}.\)
\(\frac{{10}}{3}\).
\(x - 4y + 2z + 25 = 0.\)
\(1\).
30°
\(\frac{4}{7}.\)
\(\left\{ \begin{gathered} x = - 1 \hfill \\ y = 2 + t \hfill \\ z = 2 \hfill \\\end{gathered} \right.\left( {t \in \mathbb{R}} \right)\)
\(P = 6\).
8
\(\frac{1}{4}\)
\(\frac{{{a^3}}}{6}\).
4.
\({\text{4}}\).
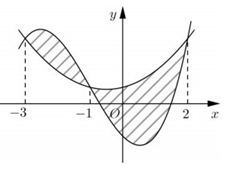
\(\frac{{253}}{{48}}\)
\(\Delta :\frac{{x - 2}}{1} = \frac{{y + 2}}{3} = \frac{{z - 1}}{4}\).
\(\ell = a.\)
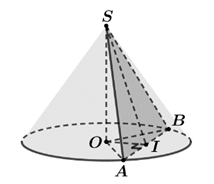 Tam giác \(SAB\) cân và có \(\widehat {SAB} = {60^0}\) nên là tam giác đều.Suy ra \(AI = \frac{1}{2}SA = \frac{R}{{\sqrt 3 }}.\)Trong tam giác vuông \(OIA,\) ta có\(O{A^2} = O{I^2} + I{A^2} \Leftrightarrow {R^2} = {a^2} + \frac{{{R^2}}}{3} \Rightarrow R = \frac{{\sqrt 3 a}}{{\sqrt 2 }}.\)Suy ra \(\ell = SA = a\sqrt 2 .\)
Tam giác \(SAB\) cân và có \(\widehat {SAB} = {60^0}\) nên là tam giác đều.Suy ra \(AI = \frac{1}{2}SA = \frac{R}{{\sqrt 3 }}.\)Trong tam giác vuông \(OIA,\) ta có\(O{A^2} = O{I^2} + I{A^2} \Leftrightarrow {R^2} = {a^2} + \frac{{{R^2}}}{3} \Rightarrow R = \frac{{\sqrt 3 a}}{{\sqrt 2 }}.\)Suy ra \(\ell = SA = a\sqrt 2 .\)510048.
\(3x + 4y - 2 = 0\).
\({\text{3}}\).
