Đề Thi Thử Tốt Nghiệp 2022 Online Môn Toán Bám Sát Đề Tham Khảo-Đề 2
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-2022-online-mon-toan-bam-sat-de-tham-khao-de-2
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp 2022 Online Môn Toán Bám Sát Đề Tham Khảo-Đề 2
\(3 + 4i\)
\(\left( { - 1;3;0} \right)\).
\(\left( {0;2} \right)\).
\(S = 16\pi \).
\(\frac{1}{4}{x^4} + \frac{1}{2}{x^2} + C\)
 Hàm số \(y = f(x)\) có bao nhiêu điểm cực trị?
Hàm số \(y = f(x)\) có bao nhiêu điểm cực trị?4.
\(S = \left( {\frac{1}{2};2} \right)\).
\(V = 3{a^3}\sqrt 2 \)
\(\mathbb{R}\backslash \left\{ { - 4;1} \right\}.\)
\(x = 4\)
\(6\).
\(2.\)
\(\overrightarrow n = \left( {3;\,6;\, - 2} \right)\)
\(\left( {0;\, - 2;\,3} \right)\).
\(z = \frac{7}{3} - i\).
\(x = 2;y = - 1\).
\(4b - 1\).
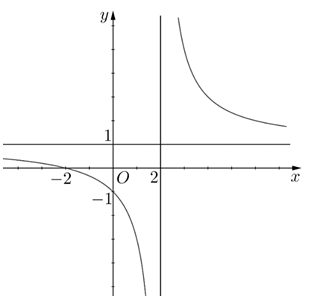
\(y = \frac{{x + 2}}{{x - 2}}\).
\(M\left( { - 2;1;3} \right)\)
\(C_8^2\).
\(\frac{{{a^3}}}{4}\)
\(y' = \frac{1}{{x\ln 10}}\)
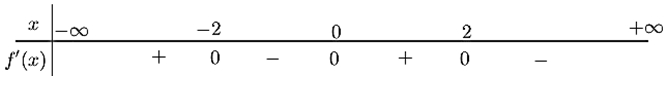 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?\(\left( { - 2;0} \right)\).
\(\pi {a^3}\).
\( - 9.\)
\(5\).
\(F\left( x \right) = {x^2} + {e^x} + 2022\).
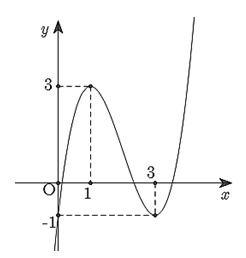 Điểm cực tiểu của hàm số đã cho là
Điểm cực tiểu của hàm số đã cho là\(x = 3\).
\(x = - 2\).
\(y = {x^3} + x\)
\({a^2} = b\).
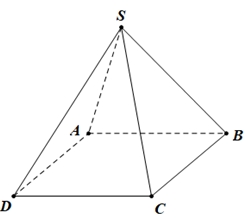 Góc giữa hai đường thẳng \(SC\) và \(AB\) bằng
Góc giữa hai đường thẳng \(SC\) và \(AB\) bằng\({60^0}\).
\(1\).
\(2x - y + 3z - 9 = 0\).
\(\sqrt {146} \).
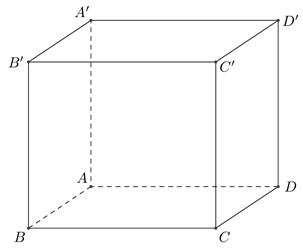
\(\sqrt 2 a\).
\(\frac{4}{{19}}\).
\(\frac{{x + 2}}{1} = \frac{{y - 1}}{{ - 3}} = \frac{{z - 3}}{5}\).
27.
\(\left[ {{{\log }_2}\left( {{x^2} + 1} \right) – {{\log }_2}\left( {x + 31} \right)} \right]\left( {32 – {2^{x – 1}}} \right) \geqslant 0\)
\( \Leftrightarrow \left[ \begin{gathered}
\left\{ \begin{gathered}
x > – 31 \hfill \\
{\log _2}\left( {{x^2} + 1} \right) \geqslant {\log _2}\left( {x + 31} \right) \hfill \\
32 \geqslant {2^{x – 1}} \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
x > – 31 \hfill \\
{\log _2}\left( {{x^2} + 1} \right) \leqslant {\log _2}\left( {x + 31} \right) \hfill \\
32 \leqslant {2^{x – 1}} \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
\left\{ \begin{gathered}
x > – 31 \hfill \\
{x^2} – x – 30 \geqslant 0 \hfill \\
x – 1 \leqslant 5 \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
x > – 31 \hfill \\
{x^2} – x – 30 \leqslant 0 \hfill \\
x – 1 \geqslant 5 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
\left\{ \begin{gathered}
x > – 31 \hfill \\
\left[ \begin{gathered}
x \leqslant – 5 \hfill \\
x \geqslant 6 \hfill \\
\end{gathered} \right. \hfill \\
x \leqslant 6 \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
x > – 31 \hfill \\
x \in \left[ { – 5;6} \right] \hfill \\
x \geqslant 6 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\) \( \Leftrightarrow \left[ \begin{gathered}
31 < x \leqslant - 5 \hfill \\
x = 6 \hfill \\
\end{gathered} \right.\)
Do \(x\) nguyên nên \(x \in \left\{ { - 30; - 29; - 28;...; - 5;6} \right\}\).
Vậy có 27 giá trị nguyên của \(x\) thỏa mãn bất phương trình đã cho.
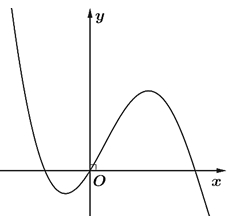 Số nghiệm thực phân biệt của phương trình \(3f\left( x \right) + 4 = 0\) là
Số nghiệm thực phân biệt của phương trình \(3f\left( x \right) + 4 = 0\) là\(2\).
Ta có \(f’\left( x \right) = 4a{x^3} + 3b{x^2} + 2cx = x\left( {4a{x^2} + 3bx + 2c} \right)\).
\(f’\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
4a{x^2} + 3bx + 2c = 0\left( 1 \right) \hfill \\
\end{gathered} \right.\).
Từ đồ thị hàm số \(y = f’\left( x \right)\) suy ra:
+) \(\mathop {\lim }\limits_{x \to – \infty } f’\left( x \right) = \mathop {\lim }\limits_{x \to – \infty } \left( {4a{x^3} + 3b{x^2} + 2cx} \right) = + \infty \Rightarrow a < 0\)
+) Đồ thị hàm số \(y = f’\left( x \right)\)cắt trục hoành tại 3 điểm phân biệt có hoành độ âm, dương, bằng 0 nên phương trình (1) sẽ có hai nghiệm \({x_1} < 0 < {x_2}\). Khi đó ta có bảng biến thiên như sau:
\(\frac{{41}}{4}\).
\(\frac{{17}}{{24}}\).
9.
\(\sqrt 5 \).
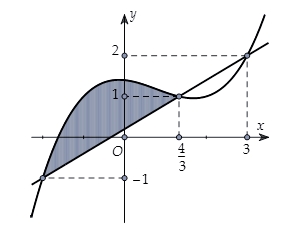 Biết diện tích hình \(S\)(được tô đậm) bằng \(\frac{{250}}{{81}}\). Tính \(\int\limits_0^2 {f\left( x \right){\text{d}}x} \).
Biết diện tích hình \(S\)(được tô đậm) bằng \(\frac{{250}}{{81}}\). Tính \(\int\limits_0^2 {f\left( x \right){\text{d}}x} \).\(\frac{{34}}{{15}}\).
\(\frac{{x + 2}}{1} = \frac{{y - 2}}{7} = \frac{{z - 5}}{3}\).
\(20\sqrt 3 \pi \).
\(7\).
\(39\).
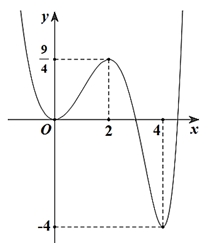 Có bao nhiêu giá trị thực của tham số \(m\)thuộc khoảng \(\left( { – 9;9} \right)\) thỏa mãn \(2m \in \mathbb{Z}\) và hàm số \(y = \left| {2f\left( {4{x^3} + 1} \right) + m – \frac{1}{2}} \right|\) có 5 điểm cực trị ?
Có bao nhiêu giá trị thực của tham số \(m\)thuộc khoảng \(\left( { – 9;9} \right)\) thỏa mãn \(2m \in \mathbb{Z}\) và hàm số \(y = \left| {2f\left( {4{x^3} + 1} \right) + m – \frac{1}{2}} \right|\) có 5 điểm cực trị ?26.
