Đề Thi Thử Tốt Nghiệp 2022 Môn Toán Online Bám Sát Đề Tham Khảo(Đề 4)
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-2022-mon-toan-online-bam-sat-de-tham-khao-de-4
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp 2022 Môn Toán Online Bám Sát Đề Tham Khảo(Đề 4)
\(\overline z = - 2 + i\).
\(( - 2; - 4; - 1)\)
\(y = - {x^2} + x - 1\).
\(V = \pi {a^3}\)
\(6x + \cos x + C\).
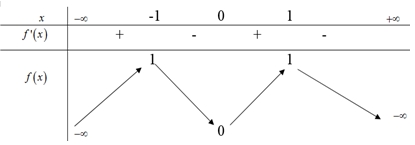 Hàm số đã cho đạt cực tiểu tại
Hàm số đã cho đạt cực tiểu tại\(x = 0\)
\(\left[ {10\,;\, + \infty } \right)\).
\(2\).
\(\log \left( {3a} \right) = \frac{1}{3}\log a\).
\(x = \frac{{10}}{3}\).
\(I = 6\).
\( - 2.\)
\(\overrightarrow n = \left( {6; - 3; - 9} \right)\).
\(I\left( {\, - 2;8;8\,} \right)\).
\(\frac{1}{{\sqrt 5 }}\).
\(y = - 3\).
\(P = {x^{\frac{{19}}{6}}}\).
\(A\left( {2\,;\,0} \right)\).
\({\vec u_3} = \left( {4;5; - 7} \right)\).
\(A_{10}^7\).
\(4cm\).
\(y' = \frac{{{6^x}}}{{\ln 6}}\).
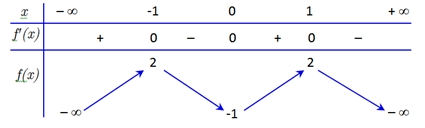 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?\(\left( {0;1} \right)\).
\(2\pi {a^3}\).
\(3\).
\({u_1} = - 1\)và \(d = - 1.\)
\(\int {f\left( x \right){\text{d}}x = \frac{{{{\text{e}}^{3x}}}}{3}} + C\).
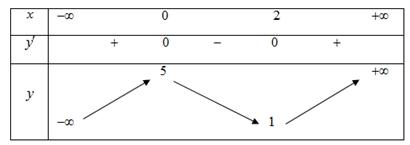
Hàm số đạt cực đại tại \(x = 0\).
\( - 29\).
\(f\left( x \right) = \frac{{2x - 1}}{{x + 1}}\).
\(3\).
\(30^\circ \).
Nên \(A'A \bot B'D'\) \( \Rightarrow \measuredangle \left( {A'A,B'D'} \right) = 90^\circ \) .
1.
\(N\left( {2;1;1} \right)\).
\(1\)
\(\frac{{4a}}{7}\).
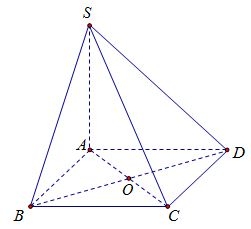 Do \(ABCD\) là hình bình hành\( \Rightarrow AC \cap BD = O\) là trung điểm của \(AC\) và \(BD\)\( \Rightarrow d\left( {C,\left( {SBD} \right)} \right) = d\left( {A,\left( {SBD} \right)} \right) = \frac{{6a}}{7}\).
Do \(ABCD\) là hình bình hành\( \Rightarrow AC \cap BD = O\) là trung điểm của \(AC\) và \(BD\)\( \Rightarrow d\left( {C,\left( {SBD} \right)} \right) = d\left( {A,\left( {SBD} \right)} \right) = \frac{{6a}}{7}\).\(\frac{{91}}{{266}}\).
\(\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 3}} = \frac{{z + 3}}{4}\)
\(3\).
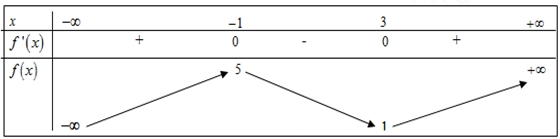 Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| – 2 = 0\) là
Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| – 2 = 0\) là\(2\).
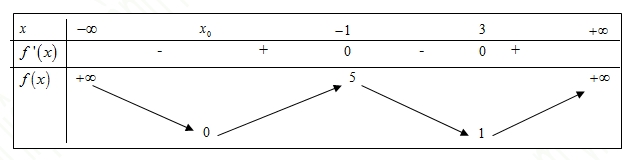 Gọi \({x_0}\)là giá trị thỏa mãn \(f\left( {{x_0}} \right) = 0\).Dựa vào bảng biến thiên của hàm số \(y = \left| {f\left( x \right)} \right|\) ta đưa ra kết luận về số nghiệm của phương trình \(\left| {f\left( x \right)} \right| – 2 = 0\) là \(4\) nghiệm.
Gọi \({x_0}\)là giá trị thỏa mãn \(f\left( {{x_0}} \right) = 0\).Dựa vào bảng biến thiên của hàm số \(y = \left| {f\left( x \right)} \right|\) ta đưa ra kết luận về số nghiệm của phương trình \(\left| {f\left( x \right)} \right| – 2 = 0\) là \(4\) nghiệm.\(3 - \ln 15\).
\(V = \frac{{{a^3}\sqrt 2 }}{6}\).
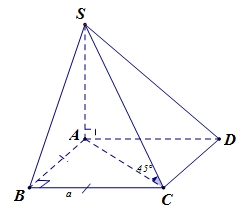 Ta có: góc giữa đường thẳng \(SC\) và \(\left( {ABCD} \right)\) là góc \(\widehat {SCA} = 45^\circ \)\( \Rightarrow SA = AC\)\( = a\sqrt 2 \).Vậy \({V_{S.ABCD}} = \frac{1}{3}.{a^2}.a\sqrt 2 \)\( = \frac{{{a^3}\sqrt 2 }}{3}\).
Ta có: góc giữa đường thẳng \(SC\) và \(\left( {ABCD} \right)\) là góc \(\widehat {SCA} = 45^\circ \)\( \Rightarrow SA = AC\)\( = a\sqrt 2 \).Vậy \({V_{S.ABCD}} = \frac{1}{3}.{a^2}.a\sqrt 2 \)\( = \frac{{{a^3}\sqrt 2 }}{3}\).\(12\).
\(\sqrt {2022} - 1\).
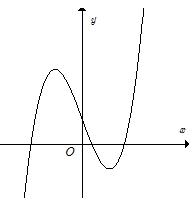
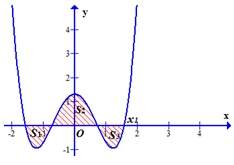 Gọi \({S_1}\), \({S_2}\), \({S_3}\) là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của \(m\) để \({S_1} + {S_3} = {S_2}\) là
Gọi \({S_1}\), \({S_2}\), \({S_3}\) là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của \(m\) để \({S_1} + {S_3} = {S_2}\) là\(\frac{5}{2}\)
\(\frac{{x - 1}}{3} = \frac{{y + 1}}{2} = \frac{z}{1}\).
\(V = \frac{{768}}{{125}}\pi \,{\text{c}}{{\text{m}}^{\text{3}}}\)
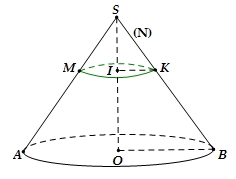 Đường sinh của hình nón lớn là: \(l = SB\)\( = \sqrt {{h^2} + {r^2}} \)\( = \sqrt {{8^2} + {6^2}} \)\( = 10\,{\text{cm}}\).Gọi \({l_2}\), \({r_2}\), \({h_2}\) lần lượt là đường sinh, bán kính đáy và chiều cao của hình nón \(\left( N \right)\).\({l_2}\, = SK = 4\,{\text{cm}}\)Ta có: \(\Delta SOB\) và \(\Delta SIK\) đồng dạng nên: \(\frac{{SI}}{{SO}} = \frac{{IK}}{{OB}} = \frac{{SK}}{{SB}} = \frac{4}{{10}} = \frac{2}{5}\).\( \Rightarrow \frac{{{h_2}}}{h} = \frac{{{r_2}}}{r} = \frac{{{l_2}}}{l} = \frac{4}{{10}} = \frac{2}{5}\)\( \Rightarrow \left[ \begin{gathered} {h_2} = \frac{2}{5}h = \frac{{16}}{5} \hfill \\ {r_2} = \frac{2}{5}.r = \frac{{12}}{5} \hfill \\ \end{gathered} \right.\).Thể tích khối nón \(\left( N \right)\)là: \({V_{(N)}} = \frac{1}{3}.\pi .r_2^2.{h_2}\)\( = \frac{1}{3}.\pi .{\left( {\frac{{12}}{5}} \right)^2}.\frac{{16}}{5}\)\( = \frac{{768}}{{125}}\pi \,{\text{c}}{{\text{m}}^{\text{3}}}\).
Đường sinh của hình nón lớn là: \(l = SB\)\( = \sqrt {{h^2} + {r^2}} \)\( = \sqrt {{8^2} + {6^2}} \)\( = 10\,{\text{cm}}\).Gọi \({l_2}\), \({r_2}\), \({h_2}\) lần lượt là đường sinh, bán kính đáy và chiều cao của hình nón \(\left( N \right)\).\({l_2}\, = SK = 4\,{\text{cm}}\)Ta có: \(\Delta SOB\) và \(\Delta SIK\) đồng dạng nên: \(\frac{{SI}}{{SO}} = \frac{{IK}}{{OB}} = \frac{{SK}}{{SB}} = \frac{4}{{10}} = \frac{2}{5}\).\( \Rightarrow \frac{{{h_2}}}{h} = \frac{{{r_2}}}{r} = \frac{{{l_2}}}{l} = \frac{4}{{10}} = \frac{2}{5}\)\( \Rightarrow \left[ \begin{gathered} {h_2} = \frac{2}{5}h = \frac{{16}}{5} \hfill \\ {r_2} = \frac{2}{5}.r = \frac{{12}}{5} \hfill \\ \end{gathered} \right.\).Thể tích khối nón \(\left( N \right)\)là: \({V_{(N)}} = \frac{1}{3}.\pi .r_2^2.{h_2}\)\( = \frac{1}{3}.\pi .{\left( {\frac{{12}}{5}} \right)^2}.\frac{{16}}{5}\)\( = \frac{{768}}{{125}}\pi \,{\text{c}}{{\text{m}}^{\text{3}}}\).\(m \in \left( {2;3} \right)\).
\(\left\{ {3;5;6;29} \right\}.\)
4.
