Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-thpt-2023-mon-toan-online-de-1
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1
\(25\).
\(\left( { - 1; - 2;5} \right).\)
Điểm \(N\left( { - 1; - 2} \right)\)
\(V = \frac{{24\pi {R^3}}}{3}\).
\(F\left( x \right) = \frac{{{x^4}}}{4} + \frac{{3{x^2}}}{2} + 2x + C\).
Hàm số \(f\left( x \right)\) có điểm cực đại là \(x = 4\).
\(S = ( - \infty ; - 3)\).
\(4\).
\(D = \left( {\frac{1}{2};\,\, + \infty } \right)\).
\(\left\{ {0;3} \right\}.\)
\(I = 6\).
\(z = 5i\).
\(\vec n = \left( {2;\,1;\, - 1} \right)\).
\(\overrightarrow a \left( { - 3;2; - 1} \right)\).
\(\left( {2; - 3} \right)\).
\(x = 2\) và \(y = 1\).
\(I = 3\).
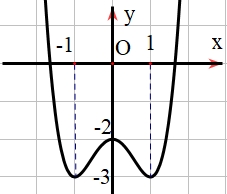
\(y = \frac{{x - 2}}{{x + 1}}\).
\(M(8;\,9;\,10)\)
\(1326.\)
\(\frac{{\sqrt 6 {a^3}}}{3}\).
\(y' = x{\pi ^{x - 1}}\).
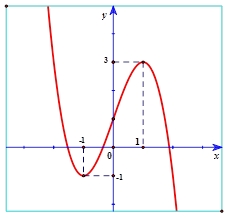 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?Hàm số đồng biến trên khoảng \(\left( { - 1;1} \right).\)
\(\frac{{16}}{3}\pi {a^3}\).
\(32\) .
\(402.\)
\(\int {\sin 2xdx = 2\cos 2x + C,C \in \mathbb{R}} \).
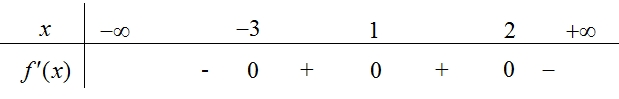 Số điểm cực trị của hàm số \(y = f(x)\) là
Số điểm cực trị của hàm số \(y = f(x)\) là\(3\).
\(\frac{4}{3}\).
\(y = \frac{{x - 1}}{{x + 2}}\).
\(\log a + 2\log b\).
\(45^\circ \).
\(1\).
\(2x + y + 3z - 4 = 0\).
\(8\).
\(h = \frac{a}{2}\).
\(0,4\).
\(d:\frac{{x - 2}}{2} = \frac{{y + 1}}{{ - 3}} = \frac{{z - 3}}{1}\)
\(8\).
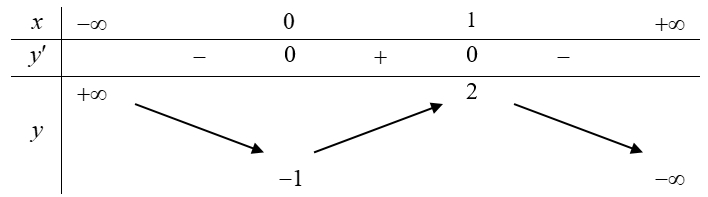 Số nghiệm của phương trình \(f\left( {2 – x} \right) – 1 = 0\) là
Số nghiệm của phương trình \(f\left( {2 – x} \right) – 1 = 0\) là\(3\).
\(12\).
\(\frac{{\sqrt 2 }}{3}{a^3}\).
\(0\).
\(M = 1 + \sqrt {13} \)
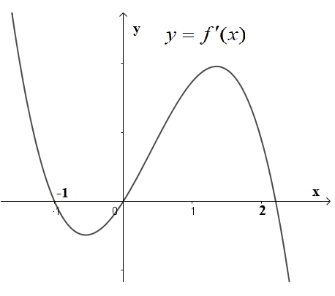
\(a + c > 0\).
\(\Delta :\left\{ \begin{gathered} x = 2 + 2t \hfill \\ y = 2 - t \hfill \\ z = - t \hfill \\ \end{gathered} \right.\).
\(V = \frac{{\pi {a^3}}}{6}\).
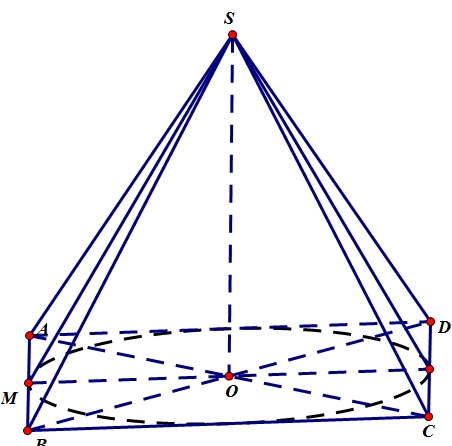 Gọi \(O\) là tâm của hình bình hành \(ABCD\) \( \Rightarrow SO \bot \left( {ABCD} \right)\).Ta có : \(OA = \frac{1}{2}AC\) \( = a\) \( \Rightarrow SO = \sqrt {S{A^2} – A{O^2}} \) \( = a\).Hình nón đỉnh \(S\) có chiều cao \(h = SO\) \( = a\), bán kính đáy \(r = \frac{{a\sqrt 2 }}{2}\), có thể tích là :\(V = \frac{1}{3}{\text{\pi }}{r^2}h\) \( = \frac{{{\text{\pi }}{a^3}}}{6}\).
Gọi \(O\) là tâm của hình bình hành \(ABCD\) \( \Rightarrow SO \bot \left( {ABCD} \right)\).Ta có : \(OA = \frac{1}{2}AC\) \( = a\) \( \Rightarrow SO = \sqrt {S{A^2} – A{O^2}} \) \( = a\).Hình nón đỉnh \(S\) có chiều cao \(h = SO\) \( = a\), bán kính đáy \(r = \frac{{a\sqrt 2 }}{2}\), có thể tích là :\(V = \frac{1}{3}{\text{\pi }}{r^2}h\) \( = \frac{{{\text{\pi }}{a^3}}}{6}\).\(S = 35\).
\(\frac{{\sqrt 7 }}{2}\) .
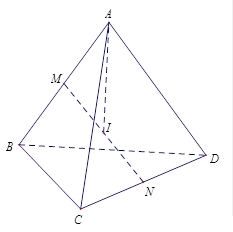 Đặt \(BC = a\); \(CA = b\); \(AB = c\) .Gọi \(M\), \(N\) lần lượt là trrung điểm của \(AB\) và \(CD\).Theo giả thiết ta có tam giác \(\Delta ABC = \Delta CDA\) \(\left( {c.c.c} \right)\)\( \Rightarrow CM = DM\) hay tam giác \(CMD\) cân tại \(M\) \( \Rightarrow MN \bot CD\).Chứng minh tương tự ta cũng có \(MN \bot AB\).Gọi \(I\) là trung điểm của \(MN\) thì \(IA = IB\) và \(IC = ID\).Mặt khác ta lại có \(AB = CD\) nên \(\Delta BMI = \Delta CNI\) \( \Rightarrow IB = IC\) hay \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).Ta có \(I{A^2} = I{M^2} + A{M^2}\)\( = \frac{{M{N^2}}}{4} + \frac{{A{B^2}}}{4}\)\( = \frac{{M{N^2} + {c^2}}}{4}\).Mặt khác \(CM\) là đường trung tuyến của tam giác \(ABC\) nên \(C{M^2} = \frac{{2{a^2} + 2{b^2} – {c^2}}}{4}\) \( \Rightarrow M{N^2} = C{I^2} – C{N^2}\)\( = \frac{{2{a^2} + 2{b^2} – {c^2}}}{4} – \frac{{{c^2}}}{4}\)\( = \frac{{{a^2} + {b^2} – {c^2}}}{2}\).Vậy \(I{A^2} = \frac{{{a^2} + {b^2} + {c^2}}}{8}\).Với \({a^2} + {b^2} + {c^2} = 2{m^2} + 2{\left( {m – 1} \right)^2} + 2{\left( {m + 4} \right)^2}\)\( = 6{\left( {m + 1} \right)^2} + 28\)Vậy \(I{A^2} = \frac{{6{{\left( {m + 1} \right)}^2} + 28}}{8} \geqslant \frac{7}{2}\)\( \Rightarrow I{A_{\min }} = \sqrt {\frac{7}{2}} = \frac{{\sqrt {14} }}{2}\).
Đặt \(BC = a\); \(CA = b\); \(AB = c\) .Gọi \(M\), \(N\) lần lượt là trrung điểm của \(AB\) và \(CD\).Theo giả thiết ta có tam giác \(\Delta ABC = \Delta CDA\) \(\left( {c.c.c} \right)\)\( \Rightarrow CM = DM\) hay tam giác \(CMD\) cân tại \(M\) \( \Rightarrow MN \bot CD\).Chứng minh tương tự ta cũng có \(MN \bot AB\).Gọi \(I\) là trung điểm của \(MN\) thì \(IA = IB\) và \(IC = ID\).Mặt khác ta lại có \(AB = CD\) nên \(\Delta BMI = \Delta CNI\) \( \Rightarrow IB = IC\) hay \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).Ta có \(I{A^2} = I{M^2} + A{M^2}\)\( = \frac{{M{N^2}}}{4} + \frac{{A{B^2}}}{4}\)\( = \frac{{M{N^2} + {c^2}}}{4}\).Mặt khác \(CM\) là đường trung tuyến của tam giác \(ABC\) nên \(C{M^2} = \frac{{2{a^2} + 2{b^2} – {c^2}}}{4}\) \( \Rightarrow M{N^2} = C{I^2} – C{N^2}\)\( = \frac{{2{a^2} + 2{b^2} – {c^2}}}{4} – \frac{{{c^2}}}{4}\)\( = \frac{{{a^2} + {b^2} – {c^2}}}{2}\).Vậy \(I{A^2} = \frac{{{a^2} + {b^2} + {c^2}}}{8}\).Với \({a^2} + {b^2} + {c^2} = 2{m^2} + 2{\left( {m – 1} \right)^2} + 2{\left( {m + 4} \right)^2}\)\( = 6{\left( {m + 1} \right)^2} + 28\)Vậy \(I{A^2} = \frac{{6{{\left( {m + 1} \right)}^2} + 28}}{8} \geqslant \frac{7}{2}\)\( \Rightarrow I{A_{\min }} = \sqrt {\frac{7}{2}} = \frac{{\sqrt {14} }}{2}\).
\(1\).
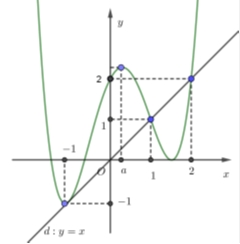 Từ đồ thị hàm số \(y = f'\left( x \right)\) và đồ thị hàm số \(y = x\) ta thấy \(f'\left( x \right) – x > 0\) với \(\forall x \in \left( { – \infty ;1} \right) \cup \left( {2; + \infty } \right)\)\(f'\left( x \right) – x < 0\) với \(\forall x \in \left( {1;2} \right)\)Ta có bảng biến thiên của \(g\left( x \right)\)
Từ đồ thị hàm số \(y = f'\left( x \right)\) và đồ thị hàm số \(y = x\) ta thấy \(f'\left( x \right) – x > 0\) với \(\forall x \in \left( { – \infty ;1} \right) \cup \left( {2; + \infty } \right)\)\(f'\left( x \right) – x < 0\) với \(\forall x \in \left( {1;2} \right)\)Ta có bảng biến thiên của \(g\left( x \right)\)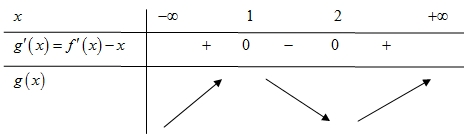 Vậy đồ thị hàm số \(y = g\left( x \right)\) có hai điểm cực trị.
Vậy đồ thị hàm số \(y = g\left( x \right)\) có hai điểm cực trị.