Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 2
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-thpt-nam-2023-mon-toan-online-de-2
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 2
\(7\)
\(R = 9\).
Điểm \(Q\left( { - 2; - 15} \right)\)
\(\frac{{128}}{3}\pi {a^3}\)
\(\int {{e^x}} dx = {e^x} + C\).
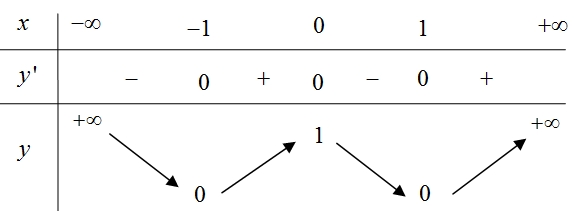 Giá trị cực đại của hàm số đã cho là
Giá trị cực đại của hàm số đã cho là\(x = 1\).
\(\left( {4; + \infty } \right)\).
\(V = 10\).
\(\mathbb{R}\backslash \left\{ { - \frac{1}{2};\frac{1}{2}} \right\}\).
\(3\).
\(1\).
\(z = - \frac{1}{{10}} + \frac{7}{{10}}i\).
\(\overrightarrow n = \left( {2;\; - 3;\;1} \right)\).
\(1\).
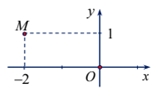
\(z = - 2 + i\).
\(x = - 5\)
\(\log a - \log b\).
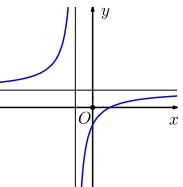
\(y = \frac{{x - 1}}{{x + 1}}.\)
\(\overrightarrow u = \left( {1;\, - 2;\,2} \right)\).
\(A_{30}^4\).
\(6{a^3}\).
\(y' = \frac{1}{{x.\log 2023}}\).
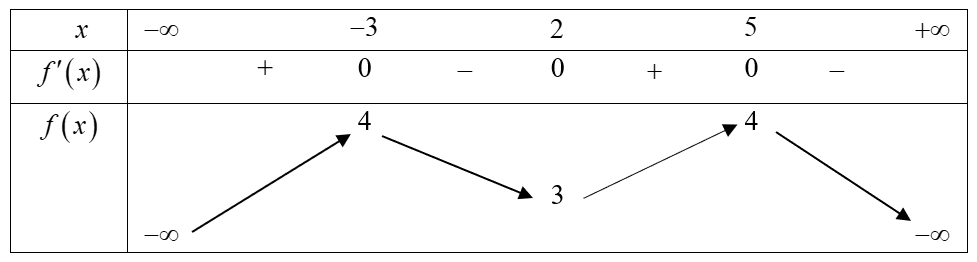 Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số đã cho đồng biến trên khoảng nào dưới đây?\(\left( {3;4} \right)\).
\(\pi {R^3}\).
\(I = 8\).
\(d = 7.\)
\(F(x) = \frac{1}{2}\ln \left| {2x + 1} \right| + C\).
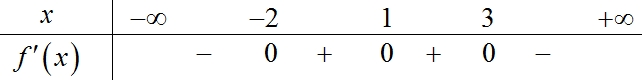 Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?\(2\).
\( - 2\)
\(y\, = \, - {x^3} + 3{x^2} - 9x + 1\).
\({a^{\frac{7}{3}}}\).
\(30^\circ \).
\(I = 13\).
\(3x + y - 2z - 4 = 0\)
\(12\).
\(\frac{{a\sqrt {10} }}{2}\).
\(\frac{2}{{25}}\).
\(\left\{ \begin{gathered} x = 1 + t \hfill \\ y = - 3 - t \hfill \\ z = 4 - 8t \hfill \\ \end{gathered} \right.\,\,\,\,\,\,\,\,\,\,t \in \mathbb{R}\).
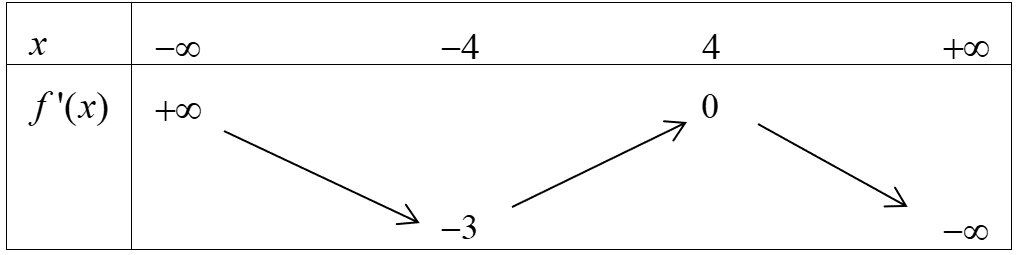 Bất phương trình \(f\left( x \right) < m - {e^{ - x}}\) đúng với mọi \(x \in \left( { - 2;2} \right)\) khi và chỉ khi
Bất phương trình \(f\left( x \right) < m - {e^{ - x}}\) đúng với mọi \(x \in \left( { - 2;2} \right)\) khi và chỉ khi\(m > f\left( 2 \right) + \frac{1}{{{e^2}}}\)
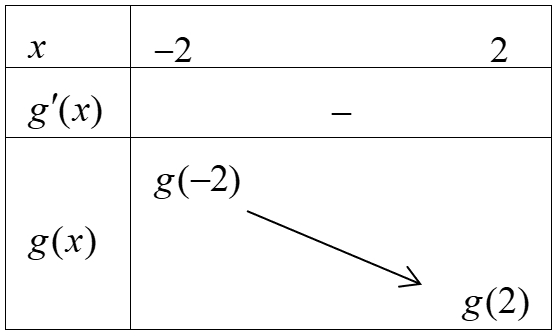 Từ bảng biến thiên ta có \(m \geqslant g( – 2) \Leftrightarrow m \geqslant f( – 2) + {e^2}\).
Từ bảng biến thiên ta có \(m \geqslant g( – 2) \Leftrightarrow m \geqslant f( – 2) + {e^2}\).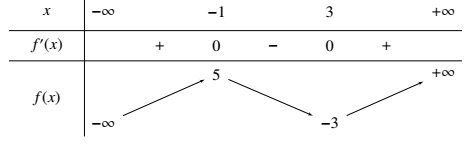 Phương trình \(\left| {f\left( {1 – 3x} \right) + 1} \right| = 3\) có bao nhiêu nghiệm?
Phương trình \(\left| {f\left( {1 – 3x} \right) + 1} \right| = 3\) có bao nhiêu nghiệm?\(4\)
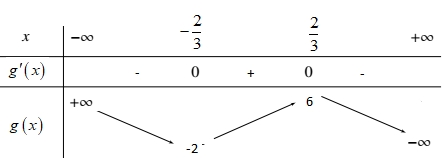 Dựa vào bảng biến thiên suy ra phương trình \(\left| {f\left( {1 – 3x} \right) + 1} \right| = 3\) có \(4\) nghiệm.
Dựa vào bảng biến thiên suy ra phương trình \(\left| {f\left( {1 – 3x} \right) + 1} \right| = 3\) có \(4\) nghiệm.\(4374\)
\(V = \frac{{{a^3}\sqrt 6 }}{{24}}\)
\(w = {2^{51}}i\).
\(m = 4\), \(n = - 4\).
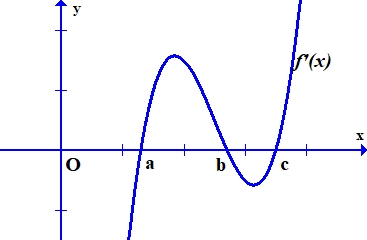 Hỏi phương trình \(f\left( x \right) = 0\) có tất cả bao nhiêu nghiệm biết \(f\left( a \right) > 0\)?
Hỏi phương trình \(f\left( x \right) = 0\) có tất cả bao nhiêu nghiệm biết \(f\left( a \right) > 0\)?\(1\).
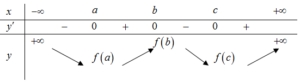
Mặt khác
\(\int\limits_a^b {f'\left( x \right){\text{d}}x} > \int\limits_b^c {f'\left( x \right){\text{d}}x} \Rightarrow \left. {f\left( x \right)} \right|_a^b > – \left. {f\left( x \right)} \right|_b^c \Leftrightarrow f\left( b \right) – f\left( a \right) > – f\left( c \right) + f\left( b \right) \Leftrightarrow f\left( a \right) < f\left( c \right)\) Mà \(f\left( a \right) > 0\) nên phương trình vô nghiệm.
\(\frac{{x + 4}}{2} = \frac{{y + 1}}{1} = \frac{{z + 5}}{{ - 1}}\)
\(8\pi {\mkern 1mu} {\mkern 1mu} {\text{d}}{{\text{m}}^3}\).
\(m = 1\)
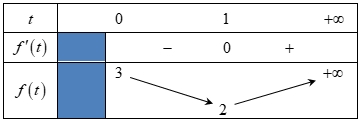 ycbt\( \Leftrightarrow 1009m \geqslant \mathop {\min }\limits_{t > 0} f\left( t \right) = 2 \Leftrightarrow m \geqslant \frac{2}{{1009}}\).Vậy \(m = 1\) là số nguyên dương nhỏ nhất thỏa yêu cầu bài toán.
ycbt\( \Leftrightarrow 1009m \geqslant \mathop {\min }\limits_{t > 0} f\left( t \right) = 2 \Leftrightarrow m \geqslant \frac{2}{{1009}}\).Vậy \(m = 1\) là số nguyên dương nhỏ nhất thỏa yêu cầu bài toán.\(S = \frac{{12}}{5}\).
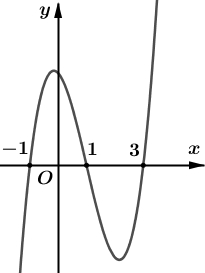
\(3\).
