Đề Thi Thử Tốt Nghiệp THPT 2023 Online Môn Toán-Đề 3
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-thpt-2023-online-mon-toan-de-3
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT 2023 Online Môn Toán-Đề 3
\( - 5i\)
\(\sqrt 7 \).
\(O\left( {0;\,0;\,0} \right)\).
\(V = \frac{{8\pi }}{3}\).
\(\int f (x)dx = 4{x^{\frac{1}{4}}} + C\).
\(2\).
\(\left( { - \infty ;\frac{1}{{25}}} \right)\).
\(\frac{{{a^3}\sqrt 3 }}{3}\).
\(\mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\).
\(x = 2\).
\( - 5\).
\(22\).
\(\overrightarrow {{n_4}} = \left( {3\,;2\,; - 6} \right)\).
\(m = - 1\).
\( - \frac{1}{2}\).
\(x = - 2,\,y = - 3\).
\(\frac{3}{{{{2022}^2}}}\).
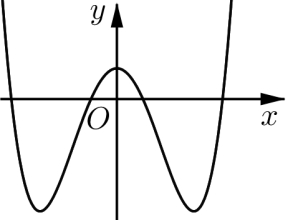
\(y = 2{x^4} - 4{x^2} + 1\).
Điểm \(P\left( { - 2;1; - 3} \right)\).
\(A_n^k = \frac{{n!}}{{(k - n)!}}\).
\(9{a^3}\).
\(y' = \frac{{{x^2}}}{{{x^2} + 2023}}\).
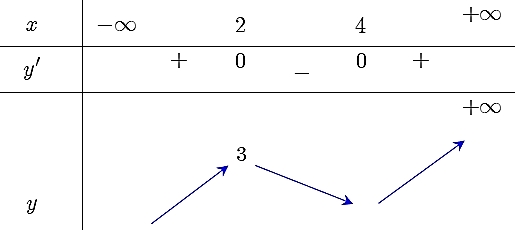 Hàm số nghịch biến trên khoảng nào sau đây?
Hàm số nghịch biến trên khoảng nào sau đây?\(\left( {4; + \infty } \right)\).
\(\frac{1}{{{l^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{R^2}}}\).
\(36\).
\(2\).
\(\int {f\left( x \right){\text{d}}x} = 2x - \frac{1}{2}\sin 2x + C\).
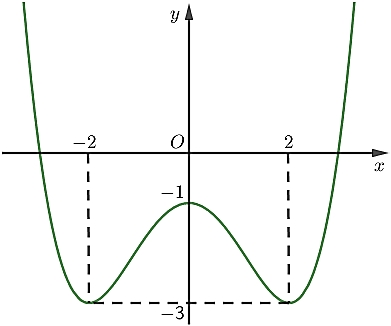
\(2\).
\( - 4\).
\(y = - 2{x^3} + 3{x^2} - 6x\).
\(a + b = 1\).
\(60^\circ \).
\(\frac{{ - 291}}{2}\).
\(\left\{ \begin{gathered} x = - 1 - t \hfill \\ y = 5 \hfill \\ z = 4 + 3t \hfill \\ \end{gathered} \right.\).
\(9\).
\(\sqrt 2 \).
\(\frac{5}{9}\).
\(\frac{{x + 1}}{1} = \frac{{y + 2}}{2} = \frac{z}{{ - 1}}\).
\(6\).
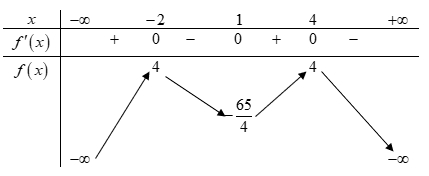 Số nghiệm thực phân biệt của phương trình là
Số nghiệm thực phân biệt của phương trình là\(11\).
\( - 1\).
\(9\sqrt 6 {a^3}\).
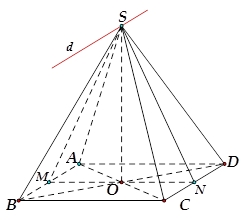 Gọi \(O = AC \cap BD\) và \(M,N\) lần lượt là trung điểm \(AB,CD\). Do \(AC = 6a \Rightarrow AB = \frac{{AC}}{{\sqrt 2 }} = 3a\sqrt 2 \). Đồng thời \(\left( {SAB} \right) \cap \left( {SCD} \right) = d\parallel \,AB\parallel CD\)Dễ dàng chứng minh \(SM \bot AB\) và \(SN \bot CD\) (do \(\Delta SAB,\Delta SCD\)cân tại \(S\)).Suy ra \(\widehat {\left[ {\left( {SAB} \right),\left( {SCD} \right)} \right]} = \widehat {\left( {SM;SN} \right)} = {60^0}\). Từ đó suy ra \(\Delta SMN\) đều hay \(SO = \frac{{MN\sqrt 3 }}{2} = \frac{{AB\sqrt 3 }}{2} = \frac{{3a\sqrt 6 }}{2}\).Vậy \({V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.\frac{{3a\sqrt 6 }}{2}.{\left( {3a\sqrt 2 } \right)^2} = 9\sqrt 6 {a^3}\).
Gọi \(O = AC \cap BD\) và \(M,N\) lần lượt là trung điểm \(AB,CD\). Do \(AC = 6a \Rightarrow AB = \frac{{AC}}{{\sqrt 2 }} = 3a\sqrt 2 \). Đồng thời \(\left( {SAB} \right) \cap \left( {SCD} \right) = d\parallel \,AB\parallel CD\)Dễ dàng chứng minh \(SM \bot AB\) và \(SN \bot CD\) (do \(\Delta SAB,\Delta SCD\)cân tại \(S\)).Suy ra \(\widehat {\left[ {\left( {SAB} \right),\left( {SCD} \right)} \right]} = \widehat {\left( {SM;SN} \right)} = {60^0}\). Từ đó suy ra \(\Delta SMN\) đều hay \(SO = \frac{{MN\sqrt 3 }}{2} = \frac{{AB\sqrt 3 }}{2} = \frac{{3a\sqrt 6 }}{2}\).Vậy \({V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.\frac{{3a\sqrt 6 }}{2}.{\left( {3a\sqrt 2 } \right)^2} = 9\sqrt 6 {a^3}\).\(2\).
\(4\sqrt {13} \).
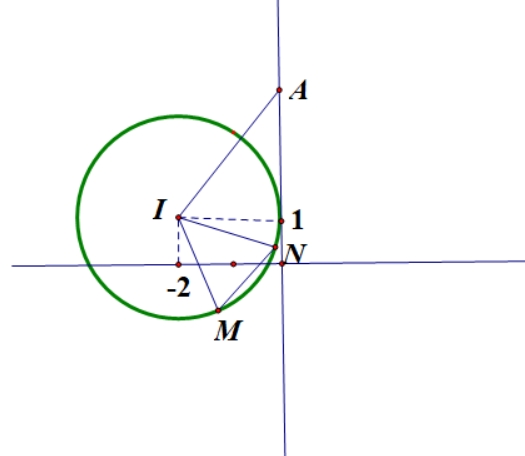
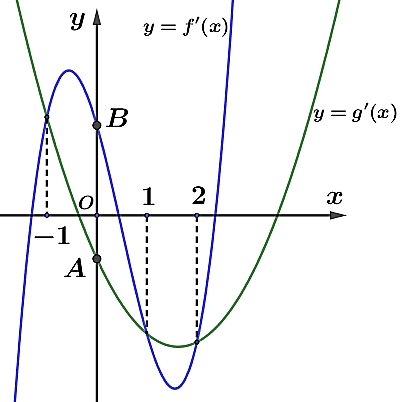
\(\frac{{512}}{{45}}\).
\(\frac{{x - 3}}{2} = \frac{y}{{ - 3}} = \frac{{z + 1}}{1}\).
\(45\pi {a^3}\).
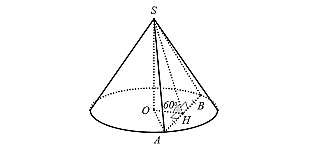 Xét hình nón đỉnh \(S\) có chiều cao \(h = SO = 3a\). Thiết diện của hình nón cắt bởi mặt phẳng \(\left( P \right)\)là tam giác \(SAB\) vuông cân tại \(S\).Kẻ \(OH \bot AB\) và \(SO \bot AB\) nên \(AB \bot \left( {SHO} \right) \Rightarrow AB \bot SH\)Vậy góc giữa mặt phẳng \(\left( P \right)\)và mặt phẳng đáy bằng \(\widehat {SHO} = {60^0}\).Xét \(\Delta OHS\)vuông tại \(O\)có \(OH = SO.\cot \widehat {SHO} = 3a.\cot {60^0} = a\sqrt 3 \); \(SH = \sqrt {O{H^2} + S{O^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {3a} \right)}^2}} = 2a\sqrt 3 \)Tam giác \(SAB\) vuông cân tại \(S\)nên suy ra \(HA = HB = HS = 2a\sqrt 3 \).Xét tam giác \(HAO\) vuông tại \(H\), ta có:\(R = OA = \sqrt {O{H^2} + H{A^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {2a\sqrt 3 } \right)}^2}} = a\sqrt {15} \)Thể tích của khối nón được giới hạn bởi hình nón là: \(V = \frac{1}{3}h.\pi {R^2} = \frac{1}{3}.3a.\pi .{\left( {a\sqrt {15} } \right)^2} = 15\pi {a^3}.\)
Xét hình nón đỉnh \(S\) có chiều cao \(h = SO = 3a\). Thiết diện của hình nón cắt bởi mặt phẳng \(\left( P \right)\)là tam giác \(SAB\) vuông cân tại \(S\).Kẻ \(OH \bot AB\) và \(SO \bot AB\) nên \(AB \bot \left( {SHO} \right) \Rightarrow AB \bot SH\)Vậy góc giữa mặt phẳng \(\left( P \right)\)và mặt phẳng đáy bằng \(\widehat {SHO} = {60^0}\).Xét \(\Delta OHS\)vuông tại \(O\)có \(OH = SO.\cot \widehat {SHO} = 3a.\cot {60^0} = a\sqrt 3 \); \(SH = \sqrt {O{H^2} + S{O^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {3a} \right)}^2}} = 2a\sqrt 3 \)Tam giác \(SAB\) vuông cân tại \(S\)nên suy ra \(HA = HB = HS = 2a\sqrt 3 \).Xét tam giác \(HAO\) vuông tại \(H\), ta có:\(R = OA = \sqrt {O{H^2} + H{A^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {2a\sqrt 3 } \right)}^2}} = a\sqrt {15} \)Thể tích của khối nón được giới hạn bởi hình nón là: \(V = \frac{1}{3}h.\pi {R^2} = \frac{1}{3}.3a.\pi .{\left( {a\sqrt {15} } \right)^2} = 15\pi {a^3}.\)\(6\).
Xét hàm số \(f\left( b \right) = {5^{{a^2}}} – {4^{ – a}}.{\left( {\frac{4}{5}} \right)^b} – 26.{\left( {\frac{1}{5}} \right)^b}\) có tập xác định \(\mathbb{R}\), và\(f'\left( b \right) = {4^{ – a}}\;{\left( {\frac{4}{5}} \right)^b}\;\ln \left( {\frac{5}{4}} \right) + 26\;{\left( {\frac{1}{5}} \right)^b}\;\ln 5 > 0\). Suy ra: \(f\left( b \right)\) đồng biến trên \(\mathbb{R}\).
Ta có: * \(f\left( {2 – {a^2}} \right) = \frac{{{5^2} – {4^{2 – a – {a^2}}} – 26}}{{{5^{2 – {a^2}}}}} = \frac{{ – 1 – {4^{2 – a – {a^2}}}}}{{{5^{2 – {a^2}}}}} < 0\)* \(f\left( {3 - {a^2}} \right) = \frac{{{5^3} - {4^{3 - a - {a^2}}} - 26}}{{{5^{3 - {a^2}}}}} = \frac{{99 - {4^{3 - a - {a^2}}}}}{{{5^{3 - {a^2}}}}} > 0\)
Do đó \(b = 2 – {a^2}\) là số nguyên lớn nhất để \(\left( * \right)\) đúng.
Theo đề: tồn tại ít nhất bốn số nguyên \(b \in \left( { – 10;10} \right)\), ta xét:
\({b_1} = – 1 – {a^2};{b_2} = – {a^2};{b_3} = 1 – {a^2};{b_4} = 2 – {a^2}\) và \({b_1},{b_2},{b_3},{b_4} \in \left( { – 10;10} \right)\)
Suy ra: \({a^2} < 9\) mà \(a \in \mathbb{Z}\) nên \(a \in \left\{ {0; \pm 1; \pm 2} \right\}\).
Vậy có 5 giá trị nguyên \(a\) thỏa mãn đề bài.
\(84\).
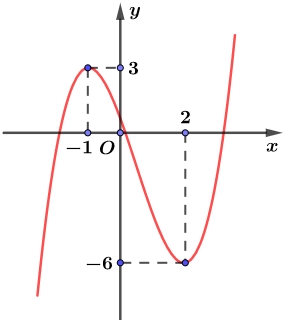 Tổng tất cả các giá trị nguyên của tham số \(m\)để hàm số \(g\left( x \right) = f\left( {\left| {{f^2}\left( x \right) – 4f\left( x \right) – m} \right|} \right)\) có \(17\) điểm cực trị là
Tổng tất cả các giá trị nguyên của tham số \(m\)để hàm số \(g\left( x \right) = f\left( {\left| {{f^2}\left( x \right) – 4f\left( x \right) – m} \right|} \right)\) có \(17\) điểm cực trị là\(1652\).
Dễ thấy \(\left( 1 \right)\) có 2 nghiệm đơn (vì có 2 cực trị) và \(\left( 2 \right)\) có 3 nghiệm đơn Vậy tổng số nghiệm đơn của phương trình \(\left( 3 \right);\,\left( 4 \right);\,\left( 5 \right)\) là 12 thì thỏa mãn
Đặt \(u = u\left( x \right) = {f^2}\left( x \right) – 4f\left( x \right) \Rightarrow u' = 2f'\left( x \right)\left( {f\left( x \right) – 2} \right) \Rightarrow u' = 0 \Leftrightarrow \left[ \begin{gathered} x \in \left\{ { – 1;2} \right\} \hfill \\ x \in \left\{ {a;b;c} \right\} \hfill \\ \end{gathered} \right.\).
Các nghiệm trên được sắp thứ tự từ nhỏ đến lớn như sau: \(a < - 1 < b < 2 < c\).
Bảng biến thiên của hàm số \(u = {f^2}\left( x \right) – 4f\left( x \right)\).
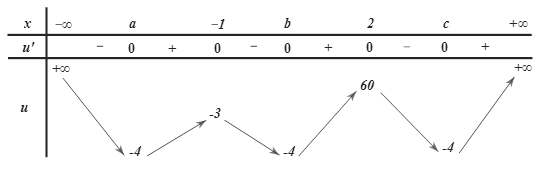 Vậy số giao điểm của các đường thẳng \(y = m – 2;y = m;y = m + 2\) với đồ thị \(u\left( x \right)\) là 12 điểm phân biệt\( \Leftrightarrow \left\{ \begin{gathered} – 3 \leqslant m – 2 < 60 \hfill \\ - 3 \leqslant m + 2 < 60 \hfill \\ \end{gathered} \right. \Leftrightarrow - 1 \leqslant m < 58 \Rightarrow m \in \left\{ { - 1;0;1;...;57} \right\} \Rightarrow S = 1652\).
Vậy số giao điểm của các đường thẳng \(y = m – 2;y = m;y = m + 2\) với đồ thị \(u\left( x \right)\) là 12 điểm phân biệt\( \Leftrightarrow \left\{ \begin{gathered} – 3 \leqslant m – 2 < 60 \hfill \\ - 3 \leqslant m + 2 < 60 \hfill \\ \end{gathered} \right. \Leftrightarrow - 1 \leqslant m < 58 \Rightarrow m \in \left\{ { - 1;0;1;...;57} \right\} \Rightarrow S = 1652\).