Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Question 1

Câu 1:

Cho số phức \(z = \sqrt 7 – 3i\). Tính \(\left| z \right|\) .

A
\(\left| z \right| = 3\).
B
\(\left| z \right| = 5\).
C
\(\left| z \right| = - 4\).
D
\(\left| z \right| = 4\).

Answer

\(\left| z \right| = - 4\).

Question 2

Câu 2:

Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \((S)\) có phương trình \({x^2} + {y^2} + {z^2} + 4x – 2y – 4 = 0\). Tính bán kính \(R\) của \((S).\)

A
\(3\).
B
\(9\).
C
\(2\).
D
\(1\).

Answer

Điểm \(M\left( {1; - 1} \right)\)

Answer

\({a^3}\).

Answer

\(\int {{x^2}} dx = 2x + C\).

Answer

\(x = - 2\).

Answer

\(x > 3\).

Answer

\(8{a^3}\).

Answer

\(\left( { - 3; + \infty } \right)\).

Answer

\(x = 65\).

Answer

\(I = 0\).

Answer

\(\bar z = 48 - 37i\).

Answer

\(\overrightarrow n = \left( { - 3;4;5} \right)\).

Answer

\(\overrightarrow a \left( {2; - 3; - 1} \right)\).

Answer

\(x = - 2\).

Answer

\(\log \left( {a{b^2}} \right) = \log a + 2\log b\).

Answer

\(y = \frac{{2x}}{{3x - 3}}\).

Answer

\(\,N\left( {0; - 1; - 2} \right)\).

Answer

\(C_{30}^3\)

Answer

\(3c{m^3}\).

Answer

\(y' = \frac{{{5^x}}}{{\ln 5}}\)

Answer

Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).

Answer

\(V = 120\pi \,{\text{c}}{{\text{m}}^3}\).

Answer

\(P = - 4\).

Answer

\(d = 4.\)

Answer

\(F(x) = \frac{1}{3}{(x + 1)^2}\).

Answer

\(2M - m = \frac{{ - 13}}{3}\).

Answer

Hàm số đồng biến trên \(\mathbb{R}\).

Answer

\(a{b^2}\).

Answer

\(90^\circ \).

Answer

\(2x + y + 3z + 6 = 0\).

Answer

\(d = \frac{{a\sqrt 5 }}{2}.\)

Answer

\(\frac{{13}}{{27}}\).

Answer

\(\left\{ \begin{gathered} x = 3 + t \hfill \\ y = 2 - t \hfill \\ z = - 1 - t \hfill \\ \end{gathered} \right.,t \in R\).

Answer

\(3\) điểm.

Answer

\(I = 8\).

Answer

\(\frac{{{a^3}\sqrt {15} }}{6}\).

Answer

\(P = 3\).

Answer

\(\sqrt {17} - 3\)

Answer

\(f\left( a \right) > f\left( c \right) > f\left( b \right)\).

Answer

\(\left\{ \begin{gathered} x = 3 + t \hfill \\ y = t \hfill \\ z = 1 \hfill \\ \end{gathered} \right.\).

Answer

\(\frac{{1200}}{{13}}\).

Answer

\(m \ne 2\).

Answer

\(\sqrt 7 \).

Question 3

Câu 3:

Điểm nào dưới đây thuộc đồ thị hàm số \(y = {x^4} – 2{x^2} + 3\) ?

A
Điểm \(N\left( { - 1;1} \right)\)
B
Điểm \(M\left( {1; - 1} \right)\)
C
Điểm \(Q\left( {0; - 3} \right)\)
D
Điểm \(P\left( { - 2;17} \right)\)

Question 4

Câu 4:

Khối cầu \(\left( S \right)\) có diện tích mặt cầu bằng \(16\pi \) (đvdt). Tính thể tích khối cầu.

A
\(6{a^3}\) .
B
\({a^3}\).
C
\(8{a^3}\).
D
\(8a\).

Question 5

Câu 5:

Họ nguyên hàm của hàm số \(f\left( x \right) = {x^2}\) là

A
\(\int {{x^2}} dx = 2x + C\).
B
\(\int {{x^2}} dx = \frac{{{x^3}}}{3}\).
C
\(\int {{x^2}} dx = \frac{{{x^2}}}{2} + C\).
D
\(\int {{x^2}} dx = \frac{{{x^3}}}{3} + C\).

Question 6

Câu 6:

Cho hàm số \(y = f\left( x \right)\) có đồ thị Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

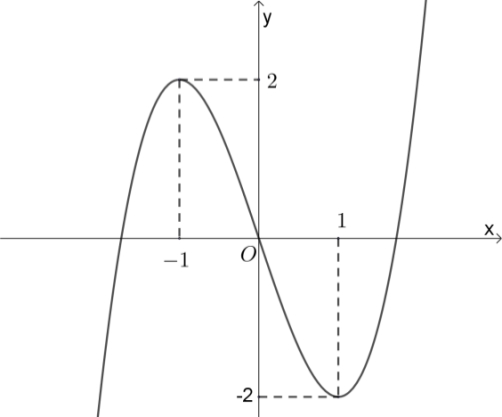Hàm số đã cho đạt cực đại tại

A
\(x = - 2\).
B
\(x = 2\).
C
\(x = - 1\).
D
\(x = 1\).

Question 7

Câu 7:

Các giá trị \(x\) thỏa mãn bất phương trình \({\log _2}\left( {3x – 1} \right) > 3\) là :

A
\(x > 3\).
B
\(x > \frac{{10}}{3}\).
C
\(\frac{1}{3} < x < 3\).
D
\(x < 3\).

Question 8

Câu 8:

Thể tích của khối lập phương cạnh \(2a\) bằng

A
\({a^3}\).
B
\(8{a^3}\).
C
\(8a\).
D
\(6{a^3}\) .

Question 9

Câu 9:

Tập xác định của hàm số \(y = {\left( {3 + x} \right)^\pi }\) là

A
\(\mathbb{R}\backslash \left\{ { - 3} \right\}\).
B
\(\mathbb{R}\).
C
\(\left( { - 3; + \infty } \right)\).
D
\(\left( { - \infty ; - 3} \right)\).

Question 10

Câu 10:

Nghiệm của phương trình \({\log _4}\left( {x – 1} \right) = 3\) là

A
\(x = 66\).
B
\(x = 63\).
C
\(x = 68\).
D
\(x = 65\).

Question 11

Câu 11:

Cho \(\int\limits_a^d {f\left( x \right){\text{d}}x} = 5\), \(\int\limits_b^d {f\left( x \right){\text{d}}x} = 2\) với \(a < d < b\). Tính \(I = \int\limits_a^b {f\left( x \right){\text{d}}x} \).

A
\(I = 0\).
B
\(I = 7.\).
C
\(I = - 3\).
D
\(I = 3\).

Question 12

Câu 12:

Cho số phức \({z_1} = 3 + 2i\), \(\,{z_2} = 6 + 5i\). Tìm số phức liên hợp của số phức \(z = 6{z_1} + 5{z_2}\)

A
\(\bar z = 51 + 40i\).
B
\(\bar z = 51 - 40i\).
C
\(\bar z = 48 + 37i\).
D
\(\bar z = 48 - 37i\).

Question 13

Câu 13:

Trong không gian với hệ toạ độ \(Oxyz\), cho phương trình mặt phẳng \(\left( P \right):\,2x – 3y + 4z + 5 = 0\). Vectơ nào sau đây là một véctơ pháp tuyến của mặt phẳng \(\left( P \right)\).

A
\(\overrightarrow n = \left( { - 4; - 3;2} \right)\).
B
\(\overrightarrow n = \left( {2; - 3;5} \right)\).
C
\(\overrightarrow n = \left( {2; - 3;4} \right)\).
D
\(\overrightarrow n = \left( { - 3;4;5} \right)\).

Question 14

Câu 14:

Trong không gian với trục hệ tọa độ \(Oxyz\), cho \(\overrightarrow a = – \overrightarrow i + 2\overrightarrow j – 3\overrightarrow k .\) Tọa độ của vectơ \(\overrightarrow a \) là:

A
\(\overrightarrow a \left( {2; - 3; - 1} \right)\).
B
\(\overrightarrow a \left( { - 3;2; - 1} \right)\).
C
\(\overrightarrow a \left( { - 1;2; - 3} \right)\).
D
\(\overrightarrow a \left( {2; - 1; - 3} \right)\).

Question 15

Câu 15:

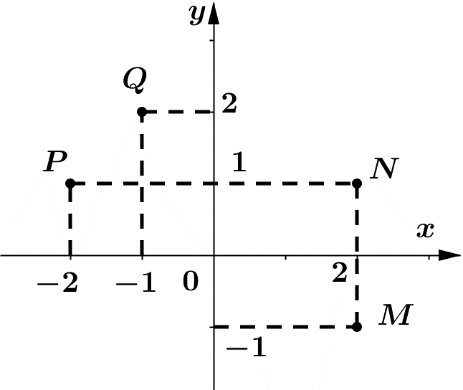
Điểm nào trong hình vẽ bên là điểm biểu diễn của số phức \(z = – 1 + 2i?\) Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

A
\(Q\).
B
\(M\).
C
\(P\).
D
\(N\).

Question 16

Câu 16:

Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x – 4}}{{x + 2}}\) là

A
\(y = 2\).
B
\(x = - 2\).
C
\(y = - 2\).
D
\(x = 2\).

Question 17

Câu 17:

Với \(a,\,b\, > 0\) tùy ý, mệnh đề nào dưới đây đúng?

A
\(\log \left( {ab} \right) = \log a.\log b\).
B
\(\log \left( {a{b^2}} \right) = 2\log a + 2\log b\).
C
\(\log \left( {a{b^2}} \right) = \log a + 2\log b\).
D
\(\log \left( {ab} \right) = \log a - \log b\).

Question 18

Câu 18:

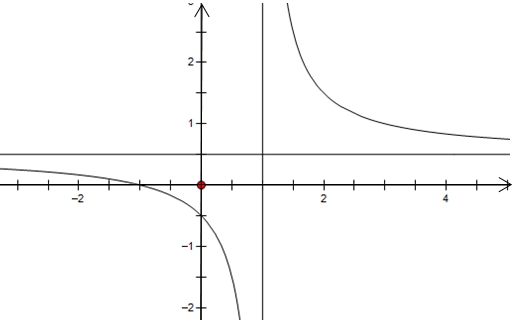
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

A
\(y = \frac{{2x - 4}}{{x - 1}}\).
B
\(y = \frac{{x + 2}}{{2x - 1}}\).
C
\(y = \frac{{2x}}{{3x - 3}}\).
D
\(y = \frac{{x + 1}}{{2x - 2}}\).

Question 19

Câu 19:

Trong không gian với hệ trục tọa độ \(Oxyz\), cho đường thẳng \(d:\frac{{x – 1}}{2} = \frac{y}{1} = \frac{{z + 1}}{2}\). Điểm nào sau đây thuộc được thẳng \(d\)?

A
\(\,M\left( {2;1;0} \right)\).
B
\(\,P\left( {3;1;1} \right)\).
C
\(\,N\left( {0; - 1; - 2} \right)\).
D
\(\,Q\left( {3;2;2} \right)\).

Question 20

Câu 20:

Cần chọn 3 người đi công tác từ một tổ có 30 người, khi đó số cách chọn là:

A
\(10\)
B
\(A_{30}^3\)
C
\({3^{30}}\)
D
\(C_{30}^3\)

Question 21

Câu 21:

Cho khối chóp có diện tích đáy bằng \(6c{m^2}\) và có chiều cao là \(2cm\). Thể tích của khối chóp đó là:

A
\(12c{m^3}\).
B
\(3c{m^3}\).
C
\(4c{m^3}\).
D
\(6c{m^3}\).

Question 22

Câu 22:

Đạo hàm của hàm số \(y = {5^x} + 2023\) là :

A
\(y' = {5^x}\)
B
\(y' = \frac{{{5^x}}}{{\ln 5}}\)
C
\(y' = {5^x}.\ln 5\)
D
\(y' = \frac{{{5^x}}}{{5\ln 5}}\)

Question 23

Câu 23:

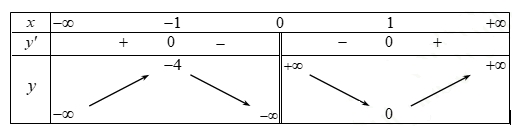
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên dưới.Mệnh đề nào sau đây đúng? Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

A
Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
B
Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
C
Hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\).
D
Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).

Question 24

Câu 24:

Tính thể tích \(V\) của khối trụ có bán kính đáy \(r = 10\,{\text{cm}}\) và chiều cao \(h = 6\,{\text{cm}}\).

A
\(V = 600\pi \,{\text{c}}{{\text{m}}^3}\).
B
\(V = 200\pi \,{\text{c}}{{\text{m}}^3}\).
C
\(V = 360\pi \,{\text{c}}{{\text{m}}^3}\).
D
\(V = 120\pi \,{\text{c}}{{\text{m}}^3}\).

Question 25

Câu 25:

Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ {0\,;\,10} \right]\) thỏa mãn \(\int\limits_0^{10} {f\left( x \right)\,{\text{d}}x} = 7\), \(\int\limits_2^6 {f\left( x \right)\,{\text{d}}x} = 3\). Tính \(P = \int\limits_0^2 {f\left( x \right)\,{\text{d}}x} + \int\limits_6^{10} {f\left( x \right)\,{\text{d}}x} \).

A
\(P = - 4\).
B
\(P = 5\).
C
\(P = 4\).
D
\(P = 7\).

Question 26

Câu 26:

Một cấp số cộng có \(8\) số hạng. Số hạng đầu là 5, số hạng thứ tám là 40. Khi đó công sai \(d\) của cấp số cộng đó là bao nhiêu?

A
\(d = 5.\)
B
\(d = 4.\)
C
\(d = 7.\)
D
\(d = 6.\)

Question 27

Câu 27:

Một nguyên hàm của hàm số \(f(x) = {(x + 1)^3}\) là

A
\(F(x) = 4{(x + 1)^4}\).
B
\(F(x) = \frac{1}{4}{(x + 1)^4}\).
C
\(F(x) = \frac{1}{3}{(x + 1)^2}\).
D
\(F(x) = 3{(x + 1)^2}\).

Question 28

Câu 28:

Cho hàm số \(y = f\left( x \right)\) có đồ thị trên một khoảng \(K\) như hình vẽ bên.

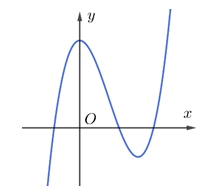
Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Trên \(K\), hàm số có bao nhiêu cực trị?

A
\(1\).
B
\(0\).
C
\(2\).
D
\(3\).

Question 29

Câu 29:

Gọi \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = \frac{{3x – 1}}{{x – 3}}\) trên đoạn \(\left[ {0\,;\,2} \right]\). Tính \(2M – m\) .

A
\(2M - m = \frac{{17}}{3}\).
B
\(2M - m = \frac{{ - 14}}{3}\).
C
\(2M - m = \frac{{ - 13}}{3}\).
D
\(2M - m = \frac{{16}}{3}\).

Question 30

Câu 30:

Cho hàm số \(y = \frac{{2x – 1}}{{x + 1}}\). Mệnh đề nào dưới đây là đúng.

A
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
B
Hàm số đồng biến trên \(\mathbb{R}\).
C
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
D
Hàm số luôn nghịch biến trên \(\mathbb{R}\).

Question 31

Câu 31:

Nếu \({\log _7}x = {\log _7}a{b^2} – {\log _7}{a^3}b\)\(\left( {a,b > 0} \right)\) thì \(x\) nhận giá trị bằng.

A
\({a^2}b\).
B
\({a^{ - 2}}b\).
C
\(a{b^2}\).
D
\({a^2}{b^2}\).

Question 32

Câu 32:

Cho khối chóp \(S.ABC\) có \(SA\, \bot \,\,\left( {ABC} \right)\), tam giác \(ABC\) vuông tại \(B\), \(AC = \,2a\), \(BC = a\),\(\,SB = 2a\sqrt 3 \). Tính góc giữa \(SA\,\)và mặt phẳng \(\,\left( {SBC} \right)\).

A
\(45^\circ \) .
B
\(90^\circ \).
C
\(30^\circ \).
D
\(60^\circ \).

Question 33

Câu 33:

Cho \(\int\limits_0^1 {\left[ {f\left( x \right) – 2g\left( x \right)} \right]{\text{d}}x} = 12\)và \(\int\limits_0^1 {g\left( x \right){\text{d}}x} = 5\), khi đó \(\int\limits_0^1 {f\left( x \right){\text{d}}x} \)bằng

A
\( - 2\).
B
\(12\).
C
\(22\).
D
\(2\).

Question 34

Câu 34:

Trong không gian với hệ tọa độ \({\text{O}}xyz\), cho điểm \(D\left( { – 2;1; – 1} \right)\) và đường thẳng \(d:\frac{{x – 1}}{2} = \frac{{y + 2}}{{ – 1}} = \frac{{z – 3}}{3}\). Mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(D\) và vuông góc \(d\) có phương trình là

A
\(2x - y + 3z - 8 = 0\).
B
\(2x - y - 3z + 2 = 0\).
C
\(2x - y + 3z + 8 = 0\).
D
\(2x + y + 3z + 6 = 0\).

Question 35

Câu 35:

Cho hai số phức \({z_1} = 2 + i\) và \({z_2} = – 3 + i\). Phần ảo của số phức \({z_1}\overline {{z_2}} \) bằng

A
\(5i\).
B
\(5\).
C
\( - 5i\).
D
\( - 5\).

Question 36

Câu 36:

Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\) và chiều cao bằng \(a\sqrt 2 \) . Tính khoảng cách \(d\) từ tâm \(O\) của đáy \(ABCD\) đến một mặt bên theo \(a\) .

A
\(d = \frac{{a\sqrt 2 }}{3}.\)
B
\(d = \frac{{a\sqrt 3 }}{2}.\)
C
\(d = \frac{{2a\sqrt 5 }}{3}.\)
D
\(d = \frac{{a\sqrt 5 }}{2}.\)

Question 37

Câu 37:

Chọn ngẫu nhiên hai số khác nhau từ 27 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng:

A
\(\frac{{13}}{{27}}\).
B
\(\frac{{14}}{{27}}\).
C
\(\frac{1}{2}\).
D
\(\frac{{365}}{{729}}\).

Question 38

Câu 38:

Trong không gian với hệ tọa độ \(Oxyz\), phương trình nào dưới đây là phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {1;0;1} \right)\) và \(B\left( {3;2; – 1} \right)\).

A
\(\left\{ \begin{gathered} x = 1 + t \hfill \\ y = 1 + t \hfill \\ z = - 1 - t \hfill \\ \end{gathered} \right.,t \in R\).
B
\(\left\{ \begin{gathered} x = 3 + t \hfill \\ y = 2 - t \hfill \\ z = - 1 - t \hfill \\ \end{gathered} \right.,t \in R\).
C
\(\left\{ \begin{gathered} x = 1 - t \hfill \\ y = - t \hfill \\ z = 1 + t \hfill \\ \end{gathered} \right.,t \in R\).
D
\(\left\{ \begin{gathered} x = 2 + t \hfill \\ y = 2 + t \hfill \\ z = - 2 - t \hfill \\ \end{gathered} \right.,t \in R\).

Question 39

Câu 39:

Số nghiệm nguyên của bất phương trình \({\left( {17 – 12\sqrt 2 } \right)^x} \geqslant {\left( {3 + \sqrt 8 } \right)^{{x^2}}}\) là

A
\(2\).
B
\(4\).
C
\(1\).
D
\(3\).

Question 40

Câu 40:

Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình bên.

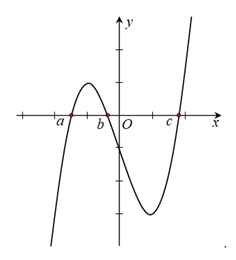
Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Biết \(f\left( a \right) > 0\), hỏi đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại nhiều nhất bao nhiêu điểm?

A
\(1\) điểm.
B
\(3\) điểm.
C
\(2\) điểm.
D
\(4\) điểm.

.

Theo hình vẽ ta có : \(\int\limits_a^b {f’\left( x \right){\text{d}}x} = \left. {\left[ {f\left( x \right)} \right]} \right|_a^b = f\left( b \right) – f\left( a \right) > 0\).
Hay : \(f\left( b \right) > f\left( a \right) > 0\).Tương tự : \(f\left( c \right) < f\left( b \right)\).Hàm số có hay hàm số có \(3\) điểm cực trị tại \(x = a,x = b,x = c\).Tóm lại, hàm số \(f\left( x \right)\) phải thỏa mãn các điều kiện sau:Hàm số có 3 điểm cực trị tại \(x = a,x = b,x = c\) thỏa \(a < b < c\).\(f\left( b \right) > f\left( a \right) > 0\).\(f\left( c \right) < f\left( b \right)\).Là hàm số bậc bốn có hệ số \(a > 0\).Từ đó, ta có thể lập được bảng biến thiên như sau : 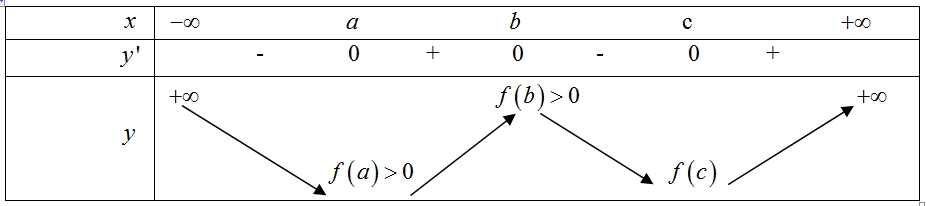Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

.Vậy đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại nhiều nhất 2 điểm.

Question 41

Câu 41:

Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có\(\int\limits_0^1 {f(x)dx = 2} \) , \(\int\limits_0^3 {f(x)dx = 6} \). Tính \(I = \int\limits_{ – 1}^1 {f\left( {\left| {2x – 1} \right|} \right)} dx\).

A
\(I = \frac{3}{2}\).
B
\(I = 4\).
C
\(I = 16\).
D
\(I = 8\).

Đặt \(t = 2x – 1 \Rightarrow dt = 2dx\).Đổi cận: \(\left\{ \begin{gathered} x = – 1 \Rightarrow t = – 3 \hfill \\ x = 1 \Rightarrow t = 1 \hfill \\ \end{gathered} \right.\)Ta có: \(I = \frac{1}{2}\int\limits_{ – 3}^1 {f\left( {\left| t \right|} \right)} dt = \frac{1}{2}\left( {\int\limits_{ – 3}^0 {f( – t) + \int\limits_0^1 {f(t)} } } \right)dt\,\,\,(1)\).+ \(\int\limits_0^1 {f(t)} dt = \int\limits_0^1 {f(x)} dx = 2\) .+ Tính \(\int\limits_{ – 3}^0 {f( – t)dt} \) : Đặt \(z = – t \Rightarrow dz = – dt \Rightarrow \int\limits_{ – 3}^0 {f( – t)dt = – } \int\limits_3^0 {f(z)dz = } \int\limits_0^3 {f(z)dz} = 6\).Thay vào (1) ta được \(I = 4\).

Question 42

Câu 42:

Cho hình chóp \(S.ABCD\) với \(ABCD\) là hình vuông cạnh \(a\). Mặt bên \(SAB\) là tam giác cân tại \(S\) và nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Cạnh bên \(SC\) tạo với đáy một góc \(60^\circ \). Tính thể tích khối chóp \(S.ABCD\).

A
\(\frac{{{a^3}\sqrt 3 }}{6}\).
B
\(\frac{{{a^3}\sqrt {15} }}{6}\).
C
\(\frac{{{a^3}\sqrt 6 }}{3}\).
D
\(\frac{{{a^3}\sqrt {15} }}{2}\).

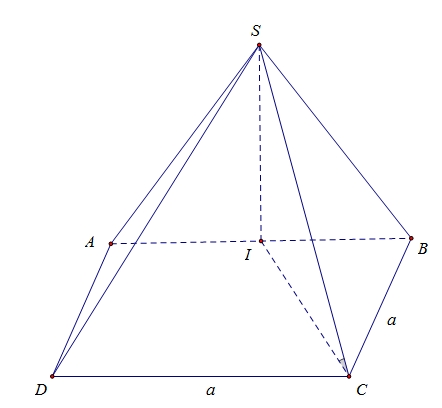Gọi \(I\) là trung điểm của \(AB\).Ta có: \(\Delta SAB\) cân tại \(S\) \( \Rightarrow \) \(SI \bot AB\) \(\left( 1 \right)\)Mặt khác: \(\left\{ \begin{gathered} \left( {SAB} \right) \bot \left( {ABCD} \right) \hfill \\ \left( {SAB} \right) \cap \left( {ABCD} \right) = AB \hfill \\ \end{gathered} \right.\) \(\left( 2 \right)\)Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra: \(SI \bot \left( {ABCD} \right)\)\( \Rightarrow SI\) là chiều cao của hình chóp \(S.ABCD\)\( \Rightarrow \)\(IC\) là hình chiếu của \(SC\) lên mặt phẳng \(\left( {ABCD} \right)\)\( \Rightarrow \widehat {\left( {SC,\left( {ABCD} \right)} \right)} = \widehat {\left( {SC,IC} \right)} = \widehat {SCI} = 60^\circ \)Xét \(\Delta IBC\) vuông tại \(B\), ta có: \(IC = \sqrt {I{B^2} + B{C^2}} = \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {a^2}} = \frac{{a\sqrt 5 }}{2}\)Xét \(\Delta SIC\) vuông tại \(I\), ta có: \(SI = IC.\tan 60^\circ = \frac{{a\sqrt 5 }}{2}.\sqrt 3 = \frac{{a\sqrt {15} }}{2}\)Vậy thể tích khối chóp \(S.ABCD\) là: \(V = \frac{1}{3}.{S_{ABCD}}.SI = \frac{1}{3}.{a^2}.\frac{{a\sqrt {15} }}{2} = \frac{{{a^3}\sqrt {15} }}{6}\).

Question 43

Câu 43:

Gọi \({z_1}\), \({z_2}\) là hai nghiệm phức của phương trình \({z^2} – z + 1 = 0\). Tính giá trị của \(P = \left| {z_1^{2023} – z_2^{2023}} \right|\).

A
\(P = 3\).
B
\(P = 2\sqrt 3 \).
C
\(P = \sqrt 3 \).
D
\(P = 0\).

\({z^2} – z + 1 = 10\)\( \Rightarrow \left[ \begin{gathered} {z_1} = \frac{1}{2} + \frac{{\sqrt 3 }}{2}i \hfill \\ {z_2} = \frac{1}{2} – \frac{{\sqrt 3 }}{2}i \hfill \\ \end{gathered} \right.\).Ta có: \({z_1}^{2023} = {\left( {\frac{{1 + \sqrt 3 i}}{2}} \right)^{2023}}\)\( = {\left[ {{{\left( {\frac{{1 + \sqrt 3 i}}{2}} \right)}^3}} \right]^{674}}\frac{{\left( {1 + \sqrt 3 i} \right)}}{2}\)\( = \frac{{{{\left( { – 8} \right)}^{674}}\left( {1 + \sqrt 3 i} \right)}}{{{2^{2023}}}}\).\({z_2}^{2023} = {\left( {\frac{{1 – \sqrt 3 i}}{2}} \right)^{2023}}\)\( = {\left[ {{{\left( {\frac{{1 – \sqrt 3 i}}{2}} \right)}^3}} \right]^{674}}\frac{{\left( {1 – \sqrt 3 i} \right)}}{2}\)\( = \frac{{{{\left( { – 8} \right)}^{674}}\left( {1 – \sqrt 3 i} \right)}}{{{2^{2023}}}}\).Suy ra: \(P = \left| {z_1^{2023} – z_2^{2023}} \right| = \left| {\frac{{{{\left( { – 8} \right)}^{674}}\left( {1 + \sqrt 3 i} \right)}}{{{2^{2023}}}} – \frac{{{{\left( { – 8} \right)}^{674}}\left( {1 – \sqrt 3 i} \right)}}{{{2^{2023}}}}} \right|\)\( = \left| {\frac{1}{{{2^{2023}}}}.{{\left( { – 8} \right)}^{674}}\left( {2\sqrt 3 i} \right)} \right| = \left| {\frac{1}{{{2^{2023}}}}{{.2}^{2022}}\left( {2\sqrt 3 i} \right)} \right| = \sqrt 3 \).

Question 44

Câu 44:

Cho số phức \(z\) thỏa mãn \(\left| {z – 1 – i} \right| = 1\), số phức \(w\) thỏa mãn \(\left| {\bar w – 2 – 3i} \right| = 2\). Tìm giá trị nhỏ nhất của \(\left| {z – w} \right|\).

A
\(\sqrt {13} - 3\)
B
\(\sqrt {17} - 3\)
C
\(\sqrt {13} + 3\)
D
\(\sqrt {17} + 3\)

Gọi \(M\left( {x;y} \right)\) biểu diễn số phức \(z = x + iy\) thì \(M\) thuộc đường tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {1;1} \right)\), bán kính \({R_1} = 1\).\(N\left( {x';y'} \right)\) biểu diễn số phức \(w = x' + iy'\) thì \(N\) thuộc đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( {2; – 3} \right)\), bán kính \({R_2} = 2\). Giá trị nhỏ nhất của \(\left| {z – w} \right|\) chính là giá trị nhỏ nhất của đoạn \(MN\).Ta có \(\overrightarrow {{I_1}{I_2}} = \left( {1; – 4} \right)\)\( \Rightarrow {I_1}{I_2} = \sqrt {17} \)\( > {R_1} + {R_2}\)\( \Rightarrow \left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) ở ngoài nhau. \( \Rightarrow M{N_{\min }}\)\( = {I_1}{I_2} – {R_1} – {R_2}\)\( = \sqrt {17} – 3\)

Question 45

Câu 45:

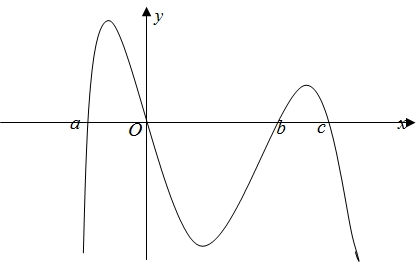
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Biết phương trình \(f'\left( x \right) = 0\) có bốn nghiệm phân biệt \(a\),\(0\),\(b\),\(c\) với \(a < 0 < b < c\). Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

A
\(f\left( b \right) > f\left( a \right) > f\left( c \right)\).
B
\(f\left( a \right) > f\left( b \right) > f\left( c \right)\).
C
\(f\left( a \right) > f\left( c \right) > f\left( b \right)\).
D
\(f\left( c \right) > f\left( a \right) > f\left( b \right)\).

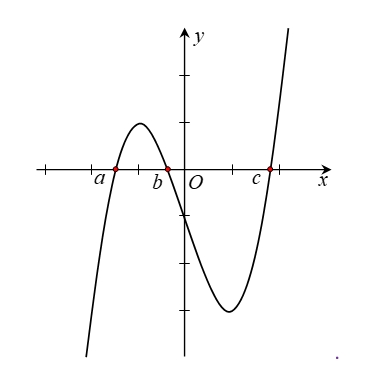
Bảng biến thiên của \(y = f\left( x \right)\): Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Do đó ta có \(f\left( c \right) > f\left( b \right)\) (1)Ta gọi \({S_1},{S_2},{S_3}\) lần lượt là các phần diện tích giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và trục hoành như hình bên.\({S_2} > {S_1} + {S_3} \Leftrightarrow – \int\limits_0^b {f'\left( x \right){\text{d}}x} > \int\limits_a^0 {f'\left( x \right){\text{d}}x} + \int\limits_b^c {f'\left( x \right){\text{d}}x} \Leftrightarrow \left. { – f\left( x \right)} \right|_0^b > \left. {f\left( x \right)} \right|_a^0 + \left. {f\left( x \right)} \right|_b^c\) \( \Leftrightarrow f\left( 0 \right) – f\left( b \right) > f\left( 0 \right) – f\left( a \right) + f\left( c \right) – f\left( b \right)\) \( \Rightarrow f\left( a \right) > f\left( c \right)\) (2)Từ (1) và (2) suy ra \(f\left( a \right) > f\left( c \right) > f\left( b \right)\).

Question 46

Câu 46:

Trong không gian với hệ toạ độ \(Oxyz\), cho đường thẳng \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( P \right):z – 1 = 0\) và \(\left( Q \right):x + y + z – 3 = 0\). Gọi \(d\) là đường thẳng nằm trong mặt phẳng \(\left( P \right)\), cắt đường thẳng \(\frac{{x – 1}}{1} = \frac{{y – 2}}{{ – 1}} = \frac{{z – 3}}{{ – 1}}\) và vuông góc với đường thẳng \(\Delta \). Phương trình của đường thẳng \(d\) là

A
\(\left\{ \begin{gathered} x = 3 + t \hfill \\ y = t \hfill \\ z = 1 + t \hfill \\ \end{gathered} \right.\).
B
\(\left\{ \begin{gathered} x = 3 - t \hfill \\ y = t \hfill \\ z = 1 \hfill \\ \end{gathered} \right.\).
C
\(\left\{ \begin{gathered} x = 3 + t \hfill \\ y = t \hfill \\ z = 1 \hfill \\ \end{gathered} \right.\).
D
\(\left\{ \begin{gathered} x = 3 + t \hfill \\ y = - t \hfill \\ z = 1 + t \hfill \\ \end{gathered} \right.\).

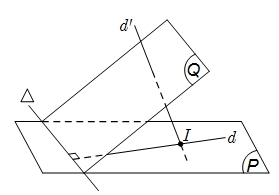Đặt \({\vec n_P} = \left( {0;0;1} \right)\) và \({\vec n_Q} = \left( {1;1;1} \right)\) lần lượt là véctơ pháp tuyến của \(\left( P \right)\) và \(\left( Q \right)\).Do \(\Delta = \left( P \right) \cap \left( Q \right)\) nên \(\Delta \) có một véctơ chỉ phương \({\vec u_\Delta } = \left[ {{{\vec n}_P},{{\vec n}_Q}} \right] = \left( { – 1;1;0} \right)\).Đường thẳng \(d\) nằm trong \(\left( P \right)\) và \(d \bot \Delta \) nên \(d\) có một véctơ chỉ phương là \({\vec u_d} = \left[ {{{\vec n}_P},{{u'}_\Delta }} \right]\) \( = \left( { – 1; – 1;0} \right)\).Gọi \(d':\frac{{x – 1}}{1} = \frac{{y – 2}}{{ – 1}} = \frac{{z – 3}}{{ – 1}}\) và \(A = d' \cap d \Rightarrow A = d' \cap \left( P \right)\)Xét hệ phương trình \(\left\{ \begin{gathered} z – 1 = 0 \hfill \\ \frac{{x – 1}}{1} = \frac{{y – 2}}{{ – 1}} = \frac{{z – 3}}{{ – 1}} \hfill \\ \end{gathered} \right.\)\( \Leftrightarrow \left\{ \begin{gathered} z = 1 \hfill \\ y = 0 \hfill \\ x = 3 \hfill \\ \end{gathered} \right.\)\( \Rightarrow A\left( {3;0;1} \right)\).Do đó phương trình đường thẳng \(d:\left\{ \begin{gathered} x = 3 + t \hfill \\ y = t \hfill \\ z = 1 \hfill \\ \end{gathered} \right.\).

Question 47

Câu 47:

Một tam giác \(ABC\) vuông tại \(A\) có \(AB = 5\), \(AC = 12\). Cho tam giác \(ABC\) quay quanh cạnh huyền \(BC\) ta được khối tròn xoay có thể tích bằng:

A
\(\frac{{1200}}{{13}}\).
B
\(\frac{{2400\pi }}{{13}}\).
C
\(\frac{{1200\pi }}{{13}}\).
D
\(\frac{{3600\pi }}{{13}}\).

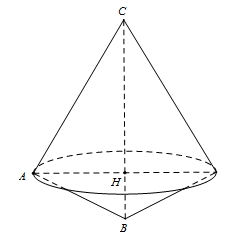Gọi \(AH\) là đường cao của tam giác \(ABC\) thì khối tròn xoay tạo thành là 2 khối nón có chung đáy với bán kính là \(R = AH = \frac{{5.12}}{{\sqrt {{5^2} + {{12}^2}} }} = \frac{{60}}{{13}}\) và các chiều cao lần lượt là \({h_1} = BH\), \({h_2} = CH\) thỏa \({h_1} + {h_2} = BC = 13\).Vậy thể tích khối tròn xoay là \(V = \frac{1}{3}\pi {R^2}\left( {{h_1} + {h_2}} \right) = \frac{1}{3}\pi {\left( {\frac{{60}}{{13}}} \right)^2}.13 = \frac{{1200\pi }}{{13}}\).

Question 48

Câu 48:

Tìm tất cả giá trị của \(m\) để bất phương trình \({9^x} – 2\left( {m + 1} \right){3^x} – 3 – 2m > 0\) nghiệm đúng với mọi số thực \(x\).

A
\(m < - \frac{3}{2}\).
B
\(m \in \left( { - 5 - 2\sqrt 3 ;\, - 5 + 2\sqrt 3 } \right)\).
C
\(m \ne 2\).
D
\(m \leqslant - \frac{3}{2}\).

Đặt \(t = {3^x}\), \(t > 0\). Khi đó, bất phương trình trở thành:\({t^2} – 2\left( {m + 1} \right)t – 3 – 2m > 0\)\( \Leftrightarrow \left( {t + 1} \right)\left( {t – 3 – 2m} \right) > 0\) \( \Leftrightarrow t – 3 – 2m > 0\)\( \Leftrightarrow t > 3 + 2m\) \(\left( 1 \right)\) (Do \(t > 0\)).Để bất phương trình đã cho nghiệm đúng với mọi \(x \in \mathbb{R}\) thì \(\left( 1 \right)\) phải nghiệm đúng với mọi \(t \in \left( {0;\, + \infty } \right)\).Điều này tương đương với \(3 + 2m \leqslant 0\) \( \Leftrightarrow m \leqslant – \frac{3}{2}\).Vậy giá trị cần tìm của \(m\) là \(m \leqslant – \frac{3}{2}\).

Question 49

Câu 49:

Trong không gian \(Oxyz\), cho điểm \(M\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};0} \right)\) và mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} = 8\). Một đường thẳng đi qua điểm \(M\) và cắt \(\left( S \right)\) tại hai điểm phân biệt \(A\), \(B\). Diện tích lớn nhất của tam giác \(OAB\) bằng

A
\(2\sqrt 2 \).
B
\(2\sqrt 7 \).
C
\(4\).
D
\(\sqrt 7 \).

Mặt cầu \(\left( S \right)\) có tâm \(O\left( {0;0;0} \right)\) và bán kính \(R = 2\sqrt 2 \).Ta có: \(\overrightarrow {OM} = \left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};0} \right)\)\( \Rightarrow OM = 1 < R\)\( \Rightarrow \) điểm \(M\) nằm trong mặt cầu \(\left( S \right)\).Gọi \(H\) là trung điểm \(AB \Rightarrow OH \leqslant OM\).Đặt \(OH = x \Rightarrow 0 \leqslant x \leqslant 1\).Đặt \(\widehat {AOH} = \alpha \Rightarrow \sin \alpha = \frac{{AH}}{{OA}} = \frac{{\sqrt {O{A^2} - O{H^2}} }}{{OA}} = \frac{{\sqrt {8 - {x^2}} }}{{2\sqrt 2 }}\); \(\cos \alpha = \frac{{OH}}{{OA}} = \frac{x}{{2\sqrt 2 }}\).Suy ra \(\sin \widehat {AOB} = 2\sin \alpha \cos \alpha = \frac{{x\sqrt {8 - {x^2}} }}{4}\).Ta có: \({S_{\Delta OAB}} = \frac{1}{2}OAOB.\sin \widehat {AOB} = x\sqrt {8 - {x^2}} \) với \(0 \leqslant x \leqslant 1\).Xét hàm số \(f\left( x \right) = x\sqrt {8 - {x^2}} \) trên đoạn \(\left[ {0;1} \right]\)\(f'\left( x \right) = \sqrt {8 - {x^2}} - \frac{{{x^2}}}{{\sqrt {8 - {x^2}} }} = \frac{{8 - 2{x^2}}}{{\sqrt {8 - {x^2}} }} > 0,\forall x \in \left[ {0;1} \right]\)\( \Rightarrow \mathop {\max }\limits_{\left[ {0;1} \right]} f\left( x \right) = f\left( 1 \right) = \sqrt 7 \)Vậy diện tích lớn nhất của tam giác \(OAB\) bằng \(\sqrt 7 \).

Question 50

Câu 50:

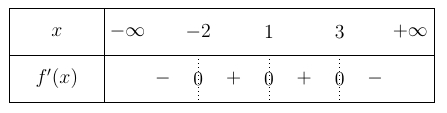Cho hàm số \(y = f\left( x \right)\)có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu \(f'\left( x \right)\) như sau Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Hỏi hàm số \(y = f\left( {{x^2} – 2x} \right)\) có bao nhiêu điểm cực tiểu?

A
\(2\).
B
\(4\).
C
\(1\).
D
\(3\).

Đặt \(g\left( x \right) = f\left( {{x^2} – 2x} \right)\). Ta có \(g'\left( x \right) = \left( {2x – 2} \right)f'\left( {{x^2} – 2x} \right)\).\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ {x^2} – 2x = – 2 \hfill \\ {x^2} – 2x = 1 \hfill \\ {x^2} – 2x = 3 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ {x^2} – 2x + 2 = 0 \hfill \\ {x^2} – 2x – 1 = 0 \hfill \\ {x^2} – 2x – 3 = 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = 1 \pm \sqrt 2 \hfill \\ x = – 1 \hfill \\ x = 3 \hfill \\ \end{gathered} \right.\).Trong đó các nghiệm \( – 1,\,\,1,\,\,3\) là nghiệm bội lẻ và \(1 \pm \sqrt 2 \) là nghiệm bội chẵn. Vì vậy hàm số \(g'\left( x \right)\) chỉ đổi dấu khi đi qua các nghiệm \( – 1,\,\,1,\,\,3\).Ta có \(g'\left( 0 \right) = – 2f'\left( 0 \right) < 0\) (do \(f'\left( 0 \right) > 0\)).Bảng xét dấu \(g'\left( x \right)\) Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Vậy hàm số \(y = f\left( {{x^2} – 2x} \right)\) có đúng \(1\) điểm cực tiểu là \(x = 1\).

Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Giải thích & Đáp án chi tiết