Đề Ôn Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 7
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-on-thi-tot-nghiep-thpt-2023-mon-toan-online-de-7
Đề Kiểm Tra: Đề Ôn Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 7
\(\sqrt 5 \).
\(r = \sqrt[{}]{2}\).
Điểm \(M( - 1;0)\).
\(36\pi \)
\(I = {3^x} + C\).
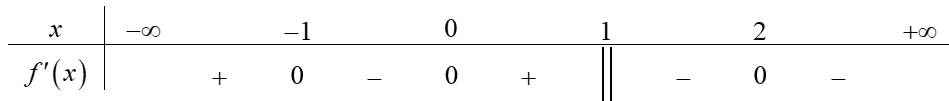 Số điểm cực đại của hàm số đã cho là
Số điểm cực đại của hàm số đã cho là\(2\).
\(x > - \frac{2}{3}\)
\(6{a^3}\).
\(D = \left( { - \infty ;2} \right)\).
\(S = \emptyset \).
\(I = 122\).
\(w = 6 - 9i\).
\(\vec n = \left( { - 2;\, - 1;\,1} \right)\).
\(\left( {3\,;\,5\,;\,1} \right)\).
\( - 1\).
\(x = - 1\); \(y = - 2\).
\(3 + {\log _a}b\)
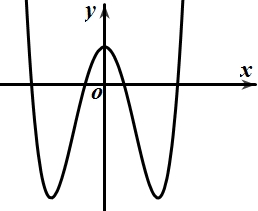
\(y = {x^4} + 2{x^2} + 1\).
\(P\left( {2;1; - 3} \right).\)
\(6!\).
\(6{a^3}\)
\(f'\left( x \right) = \frac{{3\ln 2}}{{\left( {3x - 1} \right)}}\).
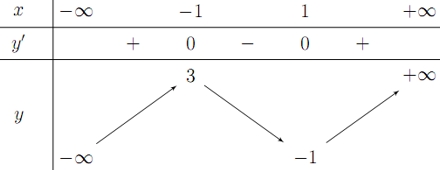 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?Hàm số đồng biến trên khoảng \(\left( { - 1;\; + \infty } \right)\).
\(S = 70{\text{\pi }}\,\left( {{\text{c}}{{\text{m}}^{\text{2}}}} \right)\).
\(I = \frac{{11}}{2}\).
\( - 2\).
\(6x + \cos x + C\).
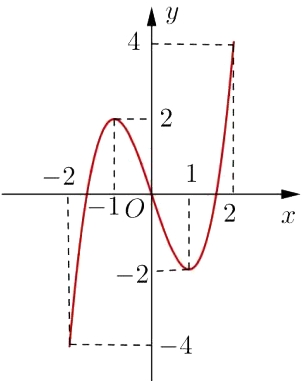
\(M\left( {1; - 2} \right)\).
\(x = 1\).
\(y = \frac{{x - 2}}{{x + 1}}\).
\(x = {a^5} + {b^3}\)
\({45^{\text{o}}}\).
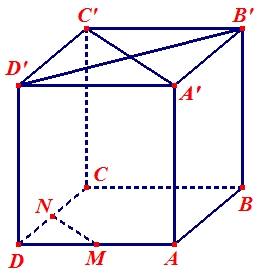 Ta có \(MN//A'C'\)mà \(A'C' \bot B'D'\)\( \Rightarrow MN \bot B'D'\).
Ta có \(MN//A'C'\)mà \(A'C' \bot B'D'\)\( \Rightarrow MN \bot B'D'\).\( - 133\).
\(2x + y - 2z + 1 = 0.\)
\(\frac{{\text{2}}}{{\text{5}}}\).
\(\frac{{a\sqrt {57} }}{{19}}\).
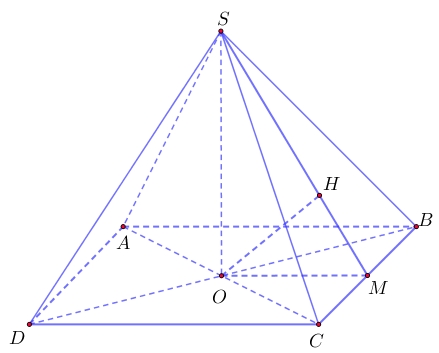 Vẽ \(OM \bot BC\)tại \(M\) thì \(\left( {SMO} \right) \bot BC\)\( \Rightarrow \left( {SMO} \right) \bot \left( {SBC} \right)\), vẽ \(OH \bot SM\) tại \(H\)\( \Rightarrow OH \bot \left( {SBC} \right)\)\( \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH\)Ta có \(AC = a\sqrt 3 \), \(OC = \frac{{a\sqrt 3 }}{2}\), \(OB = \frac{a}{2}\), \(OM.BC = OB.OC\)\( \Rightarrow OM = \frac{{OB.OC}}{{BC}}\)\( = \frac{{a\sqrt 3 }}{4}\).\(OH = \frac{{SO.MO}}{{\sqrt {S{O^2} + M{O^2}} }}\)\( = \frac{{a.\frac{{a\sqrt 3 }}{4}}}{{\sqrt {{a^2} + \frac{{3{a^2}}}{{16}}} }}\)\( = \frac{{a.\frac{{a\sqrt 3 }}{4}}}{{\sqrt {{a^2} + \frac{{3{a^2}}}{{16}}} }}\)\( = \frac{{a\sqrt {57} }}{{19}}\).
Vẽ \(OM \bot BC\)tại \(M\) thì \(\left( {SMO} \right) \bot BC\)\( \Rightarrow \left( {SMO} \right) \bot \left( {SBC} \right)\), vẽ \(OH \bot SM\) tại \(H\)\( \Rightarrow OH \bot \left( {SBC} \right)\)\( \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH\)Ta có \(AC = a\sqrt 3 \), \(OC = \frac{{a\sqrt 3 }}{2}\), \(OB = \frac{a}{2}\), \(OM.BC = OB.OC\)\( \Rightarrow OM = \frac{{OB.OC}}{{BC}}\)\( = \frac{{a\sqrt 3 }}{4}\).\(OH = \frac{{SO.MO}}{{\sqrt {S{O^2} + M{O^2}} }}\)\( = \frac{{a.\frac{{a\sqrt 3 }}{4}}}{{\sqrt {{a^2} + \frac{{3{a^2}}}{{16}}} }}\)\( = \frac{{a.\frac{{a\sqrt 3 }}{4}}}{{\sqrt {{a^2} + \frac{{3{a^2}}}{{16}}} }}\)\( = \frac{{a\sqrt {57} }}{{19}}\).\(\frac{3}{{10}}\).
\(\frac{{x - 1}}{1} = \frac{{y - 2}}{2} = \frac{z}{{ - 1}}.\)
\(3\)
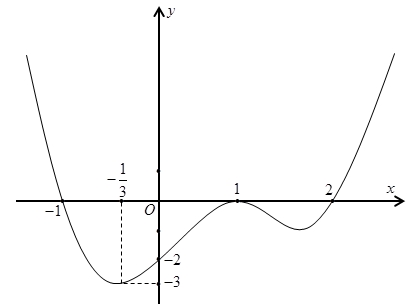 Đặt \(g\left( x \right) = f\left( {f'\left( x \right) – 1} \right).\) Gọi \(S\)là tập nghiệm của phương trình \(g'\left( x \right) = 0.\) Số phần tử của tập \(S\) là
Đặt \(g\left( x \right) = f\left( {f'\left( x \right) – 1} \right).\) Gọi \(S\)là tập nghiệm của phương trình \(g'\left( x \right) = 0.\) Số phần tử của tập \(S\) là\(9\).
\(\frac{{149}}{{225}}\).
\(V = \frac{{{a^3}\sqrt {15} }}{6}\)
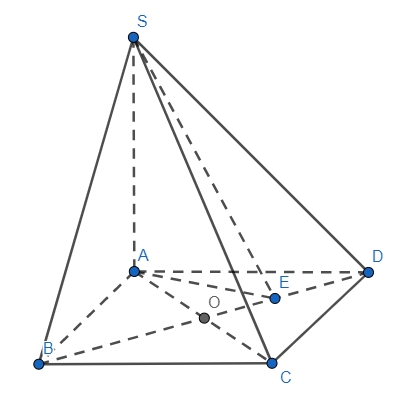 Kẻ \(AE \bot BD\)\(\left( {\widehat {\left( {SBD} \right),\left( {ABCD} \right)}} \right) = \widehat {SEA} = {60^0}\)Xét \(\Delta ABD\) vuông tại \(A\)\(AE = \frac{{AD.AB}}{{\sqrt {A{D^2} + A{B^2}} }} = \frac{{2{a^2}}}{{a\sqrt 5 }} = \frac{{2a\sqrt 5 }}{5}\)Xét \(\Delta SAE\) vuông tại \(A\)\(SA = AE.\tan {60^0} = \frac{{2a\sqrt 5 }}{5}.\sqrt 3 = \frac{{2a\sqrt {15} }}{5}\)Khi đó thể tích \(S.ABCD\)\(V = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}.\frac{{2a\sqrt {15} }}{5}.2{a^2} = \frac{{4{a^3}\sqrt {15} }}{{15}}\)
Kẻ \(AE \bot BD\)\(\left( {\widehat {\left( {SBD} \right),\left( {ABCD} \right)}} \right) = \widehat {SEA} = {60^0}\)Xét \(\Delta ABD\) vuông tại \(A\)\(AE = \frac{{AD.AB}}{{\sqrt {A{D^2} + A{B^2}} }} = \frac{{2{a^2}}}{{a\sqrt 5 }} = \frac{{2a\sqrt 5 }}{5}\)Xét \(\Delta SAE\) vuông tại \(A\)\(SA = AE.\tan {60^0} = \frac{{2a\sqrt 5 }}{5}.\sqrt 3 = \frac{{2a\sqrt {15} }}{5}\)Khi đó thể tích \(S.ABCD\)\(V = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}.\frac{{2a\sqrt {15} }}{5}.2{a^2} = \frac{{4{a^3}\sqrt {15} }}{{15}}\)\(P = - 10\).
\(\frac{{x - 1}}{3} = \frac{{y + 1}}{2} = \frac{z}{1}\)
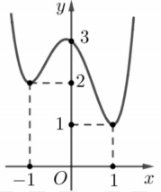 Có bao nhiêu giá trị nguyên của \(m \in \left[ { – 10;10} \right]\) để hàm số \(g\left( x \right) = \frac{1}{3}{f^3}\left( x \right) + \frac{1}{2}m.{f^2}\left( x \right) + 3f\left( x \right) – 1\) nghịch biến trên khoảng \(\left( {0;1} \right)?\)
Có bao nhiêu giá trị nguyên của \(m \in \left[ { – 10;10} \right]\) để hàm số \(g\left( x \right) = \frac{1}{3}{f^3}\left( x \right) + \frac{1}{2}m.{f^2}\left( x \right) + 3f\left( x \right) – 1\) nghịch biến trên khoảng \(\left( {0;1} \right)?\)\(15\).
\(\frac{{2\sqrt 3 }}{3}\).
\(\frac{{32}}{3}\).
\(2\).
\(3\).
\(27.\)
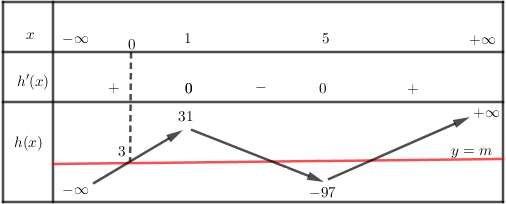 Dựa vào bảng biến thiên suy ra phương trình \(\left( 1 \right)\) có ba nghiệm dương phân biệt khi và chỉ khi \(3 < m < 31\), vậy có 27 giá trị nguyên của \(m\) thỏa yêu cầu bài toán.
Dựa vào bảng biến thiên suy ra phương trình \(\left( 1 \right)\) có ba nghiệm dương phân biệt khi và chỉ khi \(3 < m < 31\), vậy có 27 giá trị nguyên của \(m\) thỏa yêu cầu bài toán.