Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Question 1

Câu 1:

Cho số phức \(z = 3 + 2i\). Tính \(\left| z \right|\).

A
\(\left| z \right| = 13\).
B
\(\left| z \right| = \sqrt 5 \).
C
\(\left| z \right| = \sqrt {13} \).
D
\(\left| z \right| = 5\).

Answer

\(\left| z \right| = \sqrt 5 \).

Question 2

Câu 2:

Trong không gian \(Oxyz\), mặt cầu \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z + 3} \right)^2} = 4\) có tâm và bán kính lần lượt là

A
\(I\left( {1;2; - 3} \right)\), \(R = 2\).
B
\(I\left( {1;2; - 3} \right)\), \(R = 4\).
C
\(I\left( { - 1; - 2;3} \right)\), \(R = 4\).
D
\(I\left( { - 1; - 2;3} \right)\), \(R = 2\).

Answer

\(I\left( {1;2; - 3} \right)\), \(R = 2\).

Question 3

Câu 3:

Điểm nào dưới đây thuộc đồ thị hàm số \(y = {x^4} – 2{x^2} + 3\) ?

A
Điểm \(Q\left( {0; - 3} \right)\)
B
Điểm \(P\left( {2; - 11} \right)\)
C
Điểm \(N\left( { - 1;2} \right)\)
D
Điểm \(M\left( {1; - 2} \right)\)

Answer

Điểm \(P\left( {2; - 11} \right)\)

Question 4

Câu 4:

Một khối cầu có bán kính \(\frac{R}{2}\) thì có thể tích \(V\) bằng bao nhiêu?

A
\(V = \frac{{{R^3}\pi }}{2}\).
B
\(V = \frac{{{R^3}\pi }}{6}\).
C
\(V = \frac{{{R^3}\pi }}{3}\).
D
\(V = 4\pi {R^2}\).

Answer

\(V = \frac{{{R^3}\pi }}{3}\).

Question 5

Câu 5:

Một nguyên hàm của hàm số \(f(x) = 2x + 1\) là

A
\(F(x) = {x^2} + C\).
B
\(F(x) = {x^2} + x\).
C
\(F(x) = {x^2} + 1\).
D
\(F(x) = 2{x^2} + x\).

Answer

\(F(x) = {x^2} + C\).

Question 6

Câu 6:

Cho hàm số có bảng biến thiên như sau Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

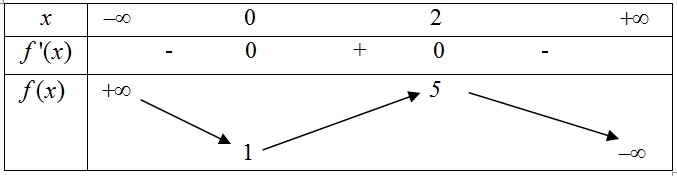Hàm số có cực đại là

A
\(y = 5\).
B
\(x = 2\).
C
\(x = 0\).
D
\(y = 1\).

Answer

\(y = 5\).

Question 7

Câu 7:

Tập nghiệm của bất phương trình \({\left( {\frac{1}{2}} \right)^x} > 4\) là

A
\(\left( { - \infty ; - 2} \right)\).
B
\(\left( { - 2; + \infty } \right)\).
C
\(\left( {2; + \infty } \right)\).
D
\(\left( { - \infty ;2} \right)\).

Answer

\(\left( { - 2; + \infty } \right)\).

Question 8

Câu 8:

Khối chóp có đáy là hình vuông cạnh \(a\) và chiều cao bằng \(4a\). Thể tích khối chóp đã cho bằng

A
\(\frac{4}{3}{a^3}\).
B
\(16{a^3}\).
C
\(\frac{{16s}}{3}{a^3}\).
D
\(4{a^3}\).

Answer

\(\frac{4}{3}{a^3}\).

Question 9

Câu 9:

Tập xác định của hàm số \(y = {\left( {1 – 2x} \right)^{\sqrt 5 }}\) là

A
\(\left( {\frac{1}{2}; + \infty } \right)\).
B
\(\left( { - \infty ;\frac{1}{2}} \right)\).
C
\(\mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\).
D
\(\mathbb{R}\).

Answer

\(\mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\).

Question 10

Câu 10:

Tập nghiệm \(S\) của phương trình \({\log _3}\left( {x – 1} \right) = 2.\)

A
\(S = \left\{ {10} \right\}\).
B
\(S = \emptyset \).
C
\(S = \left\{ 6 \right\}\)
D
\(S = \left\{ 7 \right\}\).

Answer

\(S = \left\{ {10} \right\}\).

Question 11

Câu 11:

Cho \(f\left( x \right)\), \(g\left( x \right)\) là các hàm số liên tục trên đoạn \(\left[ {a;b} \right]\) với \(a < b,\)\(\int\limits_a^b {f\left( x \right){\text{d}}x} = 3\) và \(\int\limits_a^b {g\left( x \right){\text{d}}x} = 1\). Tính \(I = \int\limits_a^b {\left[ {3f\left( x \right) - 5g\left( x \right)} \right]{\text{d}}x} \).

A
\(I = 6\).
B
\(I = 8\).
C
\(I = 4\).
D
\(I = 2\).

Answer

\(I = 4\).

Question 12

Câu 12:

Cho hai số phức \({z_1} = 2 + 3i\), \({z_2} = – 4 – 5i\). Số phức \(z = {z_1} + {z_2}\) là

A
\(z = 2 + 2i\).
B
\(z = - 2 - 2i\).
C
\(z = - 2 + 2i\).
D
\(z = 2 - 2i\).

Answer

\(z = - 2 - 2i\).

Question 13

Câu 13:

Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right)\): \( – 3x + 2z – 1 = 0\). Vectơ \(\overrightarrow n \) nào sau đây là một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\).

A
\(\overrightarrow n = \left( { - 3;2; - 1} \right)\)
B
\(\overrightarrow n = \left( { - 3;0;2} \right)\)
C
\(\overrightarrow n = \left( {3;0;2} \right)\)
D
\(\overrightarrow n = \left( {3;2; - 1} \right)\)

Answer

\(\overrightarrow n = \left( {3;0;2} \right)\)

Question 14

Câu 14:

Trong không gian \(Oxyz\), cho các vectơ \(\overrightarrow a = \left( {1;\, – 1;\,2} \right)\), \(\overrightarrow b = \left( {3;\,0;\, – 1} \right)\) và \(\overrightarrow c = \left( { – 2;\,5;\,1} \right)\). Toạ độ của vectơ \(\overrightarrow u = \overrightarrow a + \overrightarrow b – \overrightarrow c \) là:

A
\(\overrightarrow u = \left( {0;\,6;\, - 6} \right)\)
B
\(\overrightarrow u = \left( {6;\,0;\, - 6} \right)\)
C
\(\overrightarrow u = \left( {6;\, - 6;\,0} \right)\)
D
\(\overrightarrow u = \left( { - 6;\,6;\,0} \right)\)

Answer

\(\overrightarrow u = \left( {6;\,0;\, - 6} \right)\)

Question 15

Câu 15:

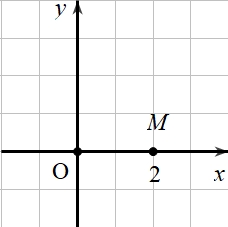
Điểm M là biểu diễn của số phức z trong hình vẽ bên dưới. Chọn khẳng định đúng Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

A
\(z = 2i\).
B
\(z = 0\).
C
\(z = 2 + 2i\).
D
\(z = 2\).

Answer

\(z = 2 + 2i\).

Question 16

Câu 16:

Đồ thị hàm số \(y = \frac{{x + 1}}{{2 – x}}\) có tiệm cận ngang là đường thẳng:

A
\(y = \frac{1}{2}.\)
B
\(x = 2.\)
C
\(y = 2.\)
D
\(y = - 1.\)

Answer

\(x = 2.\)

Question 17

Câu 17:

Với \(a\) là số thực dương, \(\log _3^2\left( {{a^2}} \right)\)bằng:

A
\(2\log _3^2a\).
B
\(\frac{4}{9}{\log _3}a\).
C
\(4\log _{_3}^2a\).
D
\(4{\log _3}a\).

Answer

\(\frac{4}{9}{\log _3}a\).

Question 18

Câu 18:

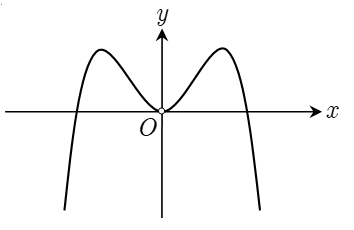
Đường cong ở hình bên là đồ thị của hàm số nào? Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

A
\(f(x) = {x^4} + 2{x^2}\).
B
\(f(x) = {x^4} - 2{x^2}\).
C
\(f(x) = - {x^4} + 2{x^2}\).
D
\(f(x) = - {x^4} + 2{x^2} - 1\).

Answer

\(f(x) = - {x^4} + 2{x^2} - 1\).

Question 19

Câu 19:

Trong không gian với hệ trục tọa độ \(Oxyz\), cho đường thẳng \(d:\left\{ \begin{gathered} x = 1 \hfill \\ y = 2 + 3t \hfill \\ z = 5 – t \hfill \\ \end{gathered} \right.\) \(\left( {t \in \mathbb{R}} \right)\). Vectơ chỉ phương của \(d\) là

A
\(\,\overrightarrow {{u_4}} = \left( {1;2;5} \right)\).
B
\(\,\overrightarrow {{u_2}} = \left( {1;3; - 1} \right)\).
C
\(\,\overrightarrow {{u_3}} = \left( {1; - 3; - 1} \right)\).
D
\(\,\overrightarrow {{u_1}} = \left( {0;3; - 1} \right)\).

Answer

\(\,\overrightarrow {{u_2}} = \left( {1;3; - 1} \right)\).

Question 20

Câu 20:

Cho \(A\) là tập hợp gồm 20 điểm phân biệt. Số đoạn thẳng có hai điểm đầu mút phân biệt thuộc tập \(A\) là:

A
\(170\)
B
\(160\)
C
\(190\)
D
\(360\)

Answer

\(\frac{{{a^3}\sqrt 3 }}{4}\).

Answer

\(y' = - \frac{4}{5}{e^{4x}}\).

Answer

\(\left( { - 1;0} \right)\).

Answer

\(36\pi {a^3}\).

Answer

\({u_4} = 8\)

Answer

\(\int f (x){\mkern 1mu} {\text{d}}x = {x^2} + \frac{1}{2}\cos 2x + C\).

Answer

\(M + 2m = 39\)

Answer

\(\left( {0; + \infty } \right)\).

Answer

\({a^5}{b^4}\).

Answer

\(\cot \varphi = 2\).

Answer

\(\left( P \right)\): \(x - y + 2z + 2 = 0\)

Answer

\(w = 10 + 10i\).

Answer

\(2\sqrt 5 a\).

Answer

\(\frac{3}{4}\).

Answer

\(\frac{{x - 2}}{{ - 1}} = \frac{{y + 4}}{3} = \frac{{z - 1}}{2}\)

Answer

\(3\sqrt 3 {a^3}\).

Answer

\(P = 2\).

Answer

\(m = 2\sqrt 2 - 2\).

Answer

\(f\left( { - 2} \right) < f\left( 2 \right) < f\left( { - 1} \right) < f\left( 6 \right)\).

Answer

\(\left\{ \begin{gathered} x = 1 - t \hfill \\ y = 2 - t \hfill \\ z = 2 \hfill \\ \end{gathered} \right.\).

Answer

\(V = 2\frac{{\pi \sqrt 2 {a^3}}}{9}\).

Answer

\(\left( {\frac{5}{3};\frac{7}{3};\frac{7}{3}} \right)\).

Question 21

Câu 21:

Cho hình lăng trụ đều \(ABC.A'B'C'\) có cạnh đáy và cạnh bên cùng bằng \(a\). Tính thể tích của khối lăng trụ đó.

A
\(\frac{{{a^3}\sqrt 6 }}{{12}}\).
B
\(\frac{{{a^3}\sqrt 6 }}{4}\).
C
\(\frac{{{a^3}\sqrt 3 }}{{12}}\).
D
\(\frac{{{a^3}\sqrt 3 }}{4}\).

Question 22

Câu 22:

Tính đạo hàm của hàm số \(y = \frac{1}{5}{e^{4x}}\).

A
\(y' = - \frac{1}{{20}}{e^{4x}}\).
B
\(y' = \frac{4}{5}{e^{4x}}\).
C
\(y' = - \frac{4}{5}{e^{4x}}\).
D
\(y' = \frac{1}{{20}}{e^{4x}}\).

Question 23

Câu 23:

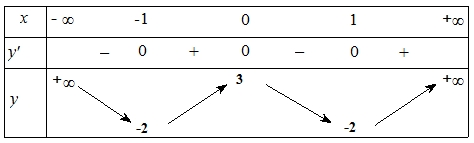Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên bên dưới. Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A
\(\left( { - 1;0} \right)\).
B
\(\left( {1; + \infty } \right)\).
C
\(\left( { - \infty ;0} \right)\).
D
\(\left( {0;1} \right)\).

Question 24

Câu 24:

Cho khối trụ tròn xoay có bán kính đáy bằng \(3a\), chiều cao bằng \(4a\), với \(0 < a \in \mathbb{R}\). Thể tích của khối trụ tròn xoay đã cho bằng

A
\(48\pi {a^3}\).
B
\(18\pi {a^3}\).
C
\(36\pi {a^3}\).
D
\(12\pi {a^3}\).

Question 25

Câu 25:

Nếu \(\int\limits_1^3 {f\left( x \right){\text{d}}x} = – 4\) thì \(\int\limits_1^3 {2f\left( x \right){\text{d}}x} \) bằng

A
\(2\)
B
\(8\)
C
\( - 8\)
D
\( - 2\)

Question 26

Câu 26:

Cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\), công sai \(d = 5\), số hạng thứ tư là

A
\({u_4} = 23\)
B
\({u_4} = 8\)
C
\({u_4} = 18\)
D
\({u_4} = 14\)

Question 27

Câu 27:

Họ nguyên hàm của hàm số \(f(x) = x – \sin 2x\) là

A
\(\int f (x){\mkern 1mu} {\text{d}}x = \frac{{{x^2}}}{2} - \frac{1}{2}\cos 2x + C\).
B
\(\int f (x){\mkern 1mu} {\text{d}}x = {x^2} + \frac{1}{2}\cos 2x + C\).
C
\(\int f (x){\mkern 1mu} {\text{d}}x = \frac{{{x^2}}}{2} + \frac{1}{2}\cos 2x + C\).
D
\(\int f (x){\mkern 1mu} {\text{d}}x = \frac{{{x^2}}}{2} + \cos 2x + C\).

Question 28

Câu 28:

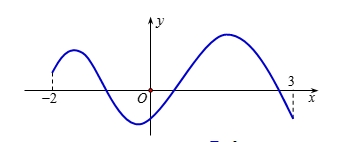Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên đoạn \(\left[ { – 2;3} \right]\) và có đồ thị là đường cong trong hình vẽ bên. Tìm số điểm cực đại của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { – 2;3} \right]\). Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

.

A
\(3\).
B
\(2\).
C
\(1\).
D
\(0\).

Question 29

Câu 29:

Gọi \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} – 3{x^2} – 9x + 35\) trên đoạn \(\left[ { – 4;4} \right]\) . Tính \(M + 2m\) .

A
\(M + 2m = - 40\)
B
\(M + 2m = - 41\)
C
\(M + 2m = 39\)
D
\(M + 2m = - 1\)

Question 30

Câu 30:

Hàm số \(f(x) = {x^4} – 2\) nghịch biến trên khoảng nào?

A
\(\left( {\frac{1}{2}; + \infty } \right)\).
B
\(\left( { - \infty ;0} \right)\).
C
\(\left( {0; + \infty } \right)\).
D
\(\left( { - \infty ;\frac{1}{2}} \right)\).

Question 31

Câu 31:

Nếu \({\log _2}x = 5{\log _2}a + 4{\log _2}b\) (\(a,b > 0\)) thì \(x\) bằng.

A
\({a^4}{b^5}\).
B
\(4a + 5b\).
C
\(5a + 4b\).
D
\({a^5}{b^4}\).

Question 32

Câu 32:

Cho hình chóp \(S.\,ABCD\) có đáy là hình vuông cạnh \(2a\), cạnh bên \(SA\) vuông góc mặt đáy và \(SA = a\). Gọi \(\varphi \) là góc tạo bởi \(SB\) và mặt phẳng \(\left( {ABCD} \right)\). Xác định \(\cot \varphi \)?

A
\(\cot \varphi = 2\).
B
\(\cot \varphi = \frac{{\sqrt 2 }}{4}\).
C
\(\cot \varphi = \frac{1}{2}\).
D
\(\cot \varphi = 2\sqrt 2 \).

Question 33

Câu 33:

Cho \(\int\limits_1^2 {\left[ {4f\left( x \right) – 2x} \right]dx} = 1\). Khi đó \(\int\limits_1^2 {f\left( x \right)} dx\)bằng :

A
\( - 1\).
B
\( - 3\).
C
\(1\).
D
\(3\).

Question 34

Câu 34:

Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d\): \(\frac{{x + 3}}{1} = \frac{{y – 2}}{{ – 1}} = \frac{{z – 1}}{2}\). Mặt phẳng \(\left( P \right)\) đi qua điểm \(M\left( {2;0; – 1} \right)\) và vuông góc với \(d\) có phương trình là

A
\(\left( P \right)\): \(x - y + 2z = 0\)
B
\(\left( P \right)\): \(x - y - 2z = 0\)
C
\(\left( P \right)\): \(2x - z = 0\)
D
\(\left( P \right)\): \(x - y + 2z + 2 = 0\)

Question 35

Câu 35:

Cho số phức \(z = 4 + 6i\). Tìm số phức \(w = i.\bar z + z\)

A
\(w = 10 - 10i\).
B
\(w = - 10 + 10i\).
C
\(w = 10 + 10i\).
D
\(w = - 2 + 10i\).

Question 36

Câu 36:

Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a\), \(AA' = 2a\). Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {A'BC} \right)\)

A
\(\frac{{3\sqrt 5 a}}{5}\).
B
\(2\sqrt 5 a\).
C
\(\frac{{\sqrt 5 a}}{5}\).
D
\(\frac{{2\sqrt 5 a}}{5}\).

Question 37

Câu 37:

Gieo đồng tiền hai lần. Xác suất để sau hai lần gieo thì mặt sấp xuất hiện ít nhất một lần

A
\(\frac{1}{4}\).
B
\(\frac{1}{2}\).
C
\(\frac{3}{4}\).
D
\(\frac{1}{3}\).

Question 38

Câu 38:

Trong không gian với hệ trục \(Oxyz\), cho tam giác \(ABC\) có \(A\left( { – 1;3;2} \right)\), \(B\left( {2;0;5} \right)\) và \(C\left( {0; – 2;1} \right)\). Phương trình trung tuyến \(AM\) của tam giác \(ABC\) là.

A
\(\frac{{x - 1}}{2} = \frac{{y + 3}}{{ - 4}} = \frac{{z + 2}}{1}\)
B
\(\frac{{x - 2}}{{ - 1}} = \frac{{y + 4}}{3} = \frac{{z - 1}}{2}\)
C
\(\frac{{x + 1}}{{ - 2}} = \frac{{y - 3}}{{ - 2}} = \frac{{z - 2}}{{ - 4}}\)
D
\(\frac{{x + 1}}{2} = \frac{{y - 3}}{{ - 4}} = \frac{{z - 2}}{1}\)

Question 39

Câu 39:

Có bao nhiêu số tự nhiên \(x\) không vượt quá \(2023\) thỏa mãn \({\log _2}\left( {\frac{x}{4}} \right)\log _2^2x \geqslant 0\)?

A
\(2021\).
B
\(2025\).
C
\(2023\).
D
\(2024\).

Điều kiện: \(x > 0\). \({\log _2}\left( {\frac{x}{4}} \right)\log _2^2x \geqslant 0\)\( \Leftrightarrow \left( {{{\log }_2}x – {{\log }_2}4} \right)\log _2^2x \geqslant 0\)\( \Leftrightarrow \left[ \begin{gathered} {\log _2}x = 0 \hfill \\ \left\{ \begin{gathered} {\log _2}x – {\log _2}4 \geqslant 0 \hfill \\ {\log _2}x \ne 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.\)\( \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ \left\{ \begin{gathered} x \geqslant 4 \hfill \\ 0 < x \ne 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x \geqslant 4 \hfill \\ \end{gathered} \right.\)(thỏa mãn điều kiện \(x > 0\)). Vậy có \(2021\) số tự nhiên \(x\) thỏa mãn bài ra.

Question 40

Câu 40:

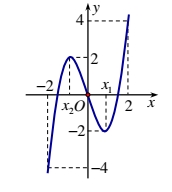Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { – 2;2} \right],\) và có đồ thị là đường cong như trong hình vẽ bên. Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Hỏi phương trình \(\left| {f\left( x \right) – 1} \right| = 2\) có bao nhiêu nghiệm phân biệt trên đoạn \(\left[ { – 2;2} \right].\)

A
\(2\).
B
\(4\).
C
\(3\).
D
\(5\).

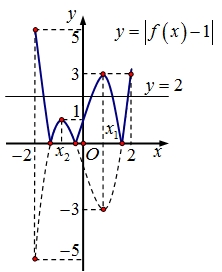* Từ hàm số \(y = f\left( x \right)\) ta suy ra đồ thị hàm số: \(y = \left| {f\left( x \right) – 1} \right|\). Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

* Số nghiệm của phương trình \(\left| {f\left( x \right) – 1} \right| = 2\) bằng số giao điểm của đồ thị hàm số: \(y = \left| {f\left( x \right) – 1} \right|\) và đường thẳng \(y = 2\).* Dựa đồ thị ta có phương trình \(\left| {f\left( x \right) – 1} \right| = 2\) có \(4\) nghiệm phân biệt trên đoạn \(\left[ { – 2;2} \right].\)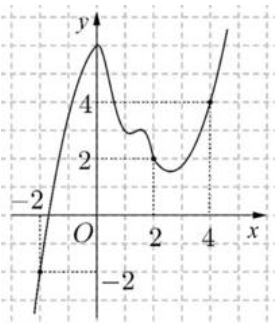

Question 41

Câu 41:

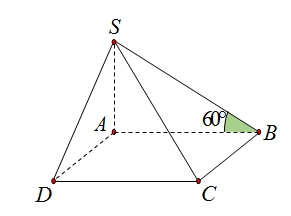Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(R\). Đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên. Khi đó giá trị của biểu thức \(\int\limits_0^4 {f'\left( {x – 2} \right)dx} + \int\limits_0^2 {f'\left( {x – 2} \right)dx} \) bằng bao nhiêu ? Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

A
\(2\).
B
\(6\).
C
\( - 2\).
D
\(10\).

\(\int\limits_0^4 {f'\left( {x – 2} \right)dx} + \int\limits_0^2 {f'\left( {x – 2} \right)dx} = \left. {f\left( {x – 2} \right)} \right|_0^4 + \left. {f\left( {x + 2} \right)} \right|_0^2 = f\left( 4 \right) – f\left( { – 2} \right) = 6\).

Question 42

Câu 42:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), góc giữa SB với mặt phẳng (ABCD) bằng \({60^0}\). Thể tích khối chóp S.ABCD là

A
\(3\sqrt 3 {a^3}\).
B
\(\sqrt 3 {a^3}\).
C
\(\frac{{{a^3}}}{{\sqrt 3 }}\).
D
\(\frac{{{a^3}}}{{3\sqrt 3 }}\).

\({S_{ABCD}} = {a^2}\); \(SA = AB.\tan {60^{\text{o}}} = a\sqrt 3 \) \({V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SA = \frac{{{a^3}}}{{\sqrt 3 }}\)

Question 43

Câu 43:

Cho các số phức \({z_1}\not = 0,\,\,{z_2}\not = 0\) thỏa mãn điều kiện \(\frac{2}{{{z_1}}} + \frac{1}{{{z_2}}} = \frac{1}{{{z_1} + {z_2}}}.\) Tính giá trị của biểu thức \(P = \left| {\frac{{{z_1}}}{{{z_2}}}} \right| + \left| {\frac{{{z_2}}}{{{z_1}}}} \right|.\).

A
\(P =\sqrt 2 \).
B
\(P =\frac{1}{{\sqrt 2 }}\).
C
\(P = 2\).
D
\(P =\frac{{3\sqrt 2 }}{2}\).

\(\frac{2}{{{z_1}}} + \frac{1}{{{z_2}}} = \frac{1}{{{z_1} + {z_2}}}\)\( \Leftrightarrow \frac{{2{z_2} + {z_1}}}{{{z_1}{z_2}}} = \frac{1}{{{z_1} + {z_2}}}\)\( \Leftrightarrow \left( {2{z_2} + {z_1}} \right)\left( {{z_1} + {z_2}} \right) – {z_1}{z_2} = 0\)\( \Leftrightarrow 2{z_1}{z_2} + 2z_2^2 + z_1^2 + {z_1}{z_2} – {z_1}{z_2} = 0\)\( \Leftrightarrow 2{z_1}{z_2} + 2z_2^2 + z_1^2 = 0\)\( \Leftrightarrow {\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^2} + 2\frac{{{z_1}}}{{{z_2}}} + 2 = 0\)\( \Leftrightarrow \left[ \begin{gathered} \frac{{{z_1}}}{{{z_2}}} = – 1 – i \hfill \\ \frac{{{z_1}}}{{{z_2}}} = – 1 + i \hfill \\ \end{gathered} \right.\)\( \Rightarrow \left| {\frac{{{z_1}}}{{{z_2}}}} \right| = \sqrt 2 \); \(\left| {\frac{{{z_2}}}{{{z_1}}}} \right| = \frac{1}{{\left| {\frac{{{z_1}}}{{{z_2}}}} \right|}} = \frac{1}{{\sqrt 2 }}\)\( \Rightarrow P = \sqrt 2 + \frac{1}{{\sqrt 2 }} = \frac{{3\sqrt 2 }}{2}\).

Question 44

Câu 44:

Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1} + 1 – i} \right| = 2\) và \({z_2} = i{z_1}\). Tìm giá trị nhỏ nhất \(m\) của biểu thức \(\left| {{z_1} – {z_2}} \right|\)?

A
\(m = \sqrt 2 - 1\).
B
\(m = 2\sqrt 2 \).
C
\(m = 2\).
D
\(m = 2\sqrt 2 - 2\).

Đặt \({z_1} = a + bi;{\text{ }}a,b \in \mathbb{R}\) \( \Rightarrow {z_2} = – b + ai\) \( \Rightarrow {z_1} – {z_2} = \left( {a + b} \right) + \left( {b – a} \right)i\).Nên \(\left| {{z_1} – {z_2}} \right| = \sqrt {{{\left( {a + b} \right)}^2} + {{\left( {b – a} \right)}^2}} = \sqrt 2 .\left| {{z_1}} \right|\)Ta lại có \(2 = \left| {{z_1} + 1 – i} \right| \leqslant \left| {{z_1}} \right| + \left| {1 – i} \right| = \left| {{z_1}} \right| + \sqrt 2 \)\( \Rightarrow \left| {{z_1}} \right| \geqslant 2 – \sqrt 2 \) . Suy ra \(\left| {{z_1} – {z_2}} \right| = \sqrt 2 .\left| {{z_1}} \right| \geqslant 2\sqrt 2 – 2\).Dấu xảy ra khi \(\frac{a}{1} = \frac{b}{{ – 1}} < 0\).Vậy \(m = \min \left| {{z_1} - {z_2}} \right| = 2\sqrt 2 - 2\).

Question 45

Câu 45:

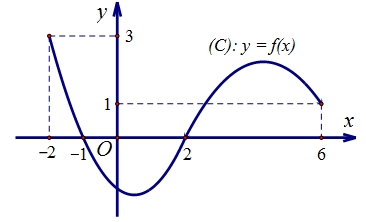
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và đồ thị của \(f'\left( x \right)\) trên đoạn \(\left[ { – 2;6} \right]\) như hình bên dưới. Khẳng định nào dưới đây đúng? Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

A
\(f\left( 6 \right) < f\left( 2 \right) < f\left( { - 2} \right) < f\left( { - 1} \right)\).
B
\(f\left( { - 2} \right) < f\left( 2 \right) < f\left( { - 1} \right) < f\left( 6 \right)\).
C
\(f\left( 2 \right) < f\left( { - 2} \right) < f\left( { - 1} \right) < f\left( 6 \right)\).
D
\(f\left( { - 2} \right) < f\left( { - 1} \right) < f\left( 2 \right) < f\left( 6 \right)\).

Dựa vào đồ thị của hàm \(f'\left( x \right)\) trên đoạn \(\left[ { – 2;6} \right]\) ta suy ra bảng biến thiên của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { – 2;6} \right]\) như sau:Dựa vào bảng biến thiên ta có \(\left\{ \begin{gathered} f\left( { – 2} \right) < f\left( { - 1} \right) \hfill \\ f\left( 2 \right) < f\left( { - 1} \right) \hfill \\ f\left( 2 \right) < f\left( 6 \right) \hfill \\ \end{gathered} \right.\) . 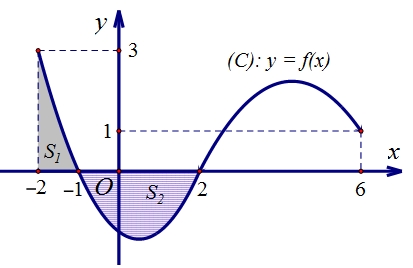Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Chỉ cần so sánh \(f\left( { – 2} \right)\) và \(f\left( 2 \right)\) nữa là xong.Gọi \({\text{cos}}\widehat {CAB} = \frac{{AC}}{{AB}} \Rightarrow AC = a\sqrt 3 \), \({S_2}\) là diện tích hình phẳng được tô đậm như trên hình vẽ.Ta có:\({S_1} = \int\limits_{ – 2}^{ – 1} {\left| {f'\left( x \right)} \right|{\text{d}}x} \)\( = \int\limits_{ – 2}^{ – 1} {f'\left( x \right)dx} \)\( = f\left( { – 1} \right) – f\left( { – 2} \right)\).\({S_2} = \int\limits_{ – 1}^2 {\left| {f'\left( x \right)} \right|{\text{d}}x} \)\( = – \int\limits_{ – 1}^2 {f'\left( x \right){\text{d}}x} \)\( = f\left( { – 1} \right) – f\left( 2 \right)\).Dựa vào đồ thị ta thấy \({S_1} < {S_2}\) nên \(f\left( { - 1} \right) - f\left( { - 2} \right) < f\left( { - 1} \right) - f\left( 2 \right)\)\( \Leftrightarrow f\left( { - 2} \right) > f\left( 2 \right)\).

Question 46

Câu 46:

Trong không gian \(Oxyz\), đường thẳng đi qua điểm \(M\left( {1;2;2} \right)\), song song với mặt phẳng \(\left( P \right):x – y + z + 3 = 0\) đồng thời cắt đường thẳng \(d:\frac{{x – 1}}{1} = \frac{{y – 2}}{1} = \frac{{z – 3}}{1}\) có phương trình là

A
\(\left\{ \begin{gathered} x = 1 - t \hfill \\ y = 2 - t \hfill \\ z = 2 \hfill \\ \end{gathered} \right.\).
B
\(\left\{ \begin{gathered} x = 1 - t \hfill \\ y = 2 - t \hfill \\ z = 3 - t \hfill \\ \end{gathered} \right.\).
C
\(\left\{ \begin{gathered} x = 1 + t \hfill \\ y = 2 - t \hfill \\ z = 3 \hfill \\ \end{gathered} \right.\).
D
\(\left\{ \begin{gathered} x = 1 - t \hfill \\ y = 2 + t \hfill \\ z = 3 \hfill \\ \end{gathered} \right.\).

Gọi đường thẳng cần tìm là \(\Delta \). Gọi \(I = \Delta \cap d\)\( \Rightarrow I \in d\) \( \Leftrightarrow I\left( {1 + t;2 + t;3 + t} \right)\).\(\overrightarrow {MI} = \left( {t;t;1 + t} \right)\) mà \(MI{\text{//}}\left( P \right)\) nên \(\overrightarrow {MI} .{\vec n_{\left( P \right)}} = 0\) \( \Leftrightarrow t – t + \left( {1 + t} \right) = 0\) \( \Leftrightarrow t = – 1\)\( \Rightarrow \overrightarrow {MI} = \left( { – 1; – 1;0} \right)\)Đường thẳng \(\Delta \) đi qua \(M\left( {1;2;2} \right)\) và \(I\) có véctơ chỉ phương là \(\overrightarrow {MI} = \left( { – 1; – 1;0} \right)\) có phương trình tham số là \(\left\{ \begin{gathered} x = 1 – t \hfill \\ y = 2 – t \hfill \\ z = 2 \hfill \\ \end{gathered} \right.\).

Question 47

Câu 47:

Một hình nón có thiết diện tạo bởi mặt phẳng qua trục của hình nón là một tam giác vuông cân với cạnh huyền bằng \(2a\sqrt 2 \). Tính thể tích \(V\) của khối nón.

A
\(V = \frac{{2\pi \sqrt 2 {a^3}}}{3}\).
B
\(V = \frac{{2\pi {a^3}}}{3}\).
C
\(V = 2\frac{{\pi \sqrt 2 {a^3}}}{9}\).
D
\(V = 2\pi \sqrt 2 {a^3}\).

Ta có tam giác \(SMN\) cân tại \(S\). Giả thiết tam giác, suy ra tam giác \(SMN\)vuông cân tại \(S\). Thiết diện qua trục nên tâm \(O\) đường tròn đáy thuộc cạnh huyền \(MN\).Vậy hình nón có bán kính đáy \(R = \frac{1}{2}MN = a\sqrt 2 \), đường cao \(h = \frac{1}{2}MN = a\sqrt 2 \).Thể tích khối nón \(V = \frac{1}{3}\pi {R^2}h = \frac{{2\pi \sqrt 2 {a^3}}}{3}\).

Question 48

Câu 48:

Có bao nhiêu giá trị nguyên dương của tham số \(m\) để bất phương trình \({9^{\sqrt {{x^2} – 3x + m} }} + {2.3^{\sqrt {{x^2} – 3x + m} – 2 + x}} < {3^{2x - 3}}\) có nghiệm?

A
\(1\)
B
\(6\)
C
\(4\)
D
\(9\)

Điều kiện \({x^2} – 3x + m \geqslant 0\) \({9^{\sqrt {{x^2} – 3x + m} }} + {2.3^{\sqrt {{x^2} – 3x + m} – 2 + x}} < {3^{2x - 3}}\)\( \Leftrightarrow {3^{2\left( {\sqrt {{x^2} - 3x + m} - x} \right)}} + \frac{2}{9}{.3^{\sqrt {{x^2} - 3x + m} - x}} - \frac{1}{{27}} < 0\)\( \Leftrightarrow 0 < {3^{\sqrt {{x^2} - 3x + m} - x}} < {3^{ - 2}}\) \( \Leftrightarrow \sqrt {{x^2} - 3x + m} - x < - 2\)\( \Leftrightarrow \sqrt {{x^2} - 3x + m} < x - 2\).\( \Leftrightarrow \left\{ \begin{gathered} {x^2} - 3x + m \geqslant 0 \hfill \\ x - 2 > 0 \hfill \\ {x^2} – 3x + m < {x^2} - 4x + 4 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow \left\{ \begin{gathered} {x^2} - 3x + m \geqslant 0 \hfill \\ x > 2 \hfill \\ x < 4 - m \hfill \\ \end{gathered} \right.\)\( \Rightarrow 4 - m > 2 \Leftrightarrow m < 2\).Do \(m\) nguyên dương nên \(m = 1\) thỏa mãn .

Question 49

Câu 49:

Trong không gian \(Oxyz\), cho mặt phẳng \((P):\;x + 2y + 2z + 4 = 0\) và mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2x – 2y – 2z – 1 = 0.\) Giá trị của điểm \(M\) trên \(\left( S \right)\) sao cho \(d\left( {M,\left( P \right)} \right)\) đạt GTNN là

A
\(\left( {1; - 2;1} \right)\).
B
\(\left( {\frac{1}{3}; - \frac{1}{3}; - \frac{1}{3}} \right)\).
C
\(\left( {\frac{5}{3};\frac{7}{3};\frac{7}{3}} \right)\).
D
\(\left( {1;1;3} \right)\).

Ta có: \(d(M,(P)) = 3 > R = 2 \Rightarrow (P) \cap (S) = \emptyset .\)Đường thẳng \(d\) đi qua \(I\) và vuông góc với \(\left( P \right)\) có pt: \(\left\{ {\begin{array}{*{20}{c}} {x = 1 + t} \\ {y = 1 + 2t} \\ {z = 1 + 2t} \end{array}} \right.,t \in \mathbb{R}.\)Tọa độ giao điểm của \(d\) và \(\left( S \right)\) là \(A\left( {\frac{5}{3};\frac{7}{3};\frac{7}{3}} \right)\), \(B\left( {\frac{1}{3}; – \frac{1}{3}; – \frac{1}{3}} \right)\)Ta có: \(d(A,(P)) = 5 \geqslant d(B,(P)) = 1.\) \( \Rightarrow d(A,(P)) \geqslant d(M,(P)) \geqslant d(B,(P)).\)Vậy: \( \Rightarrow d{(M,(P))_{\min }} = 1 \Leftrightarrow M \equiv B.\)

Question 50

Câu 50:

Cho hàm số \(y = f\left( x \right)\) và đồ thị hình bên là đồ thị của đạo hàm \(f'\left( x \right)\).

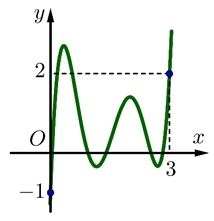
Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Hỏi đồ thị của hàm số \(g\left( x \right) = \left| {2f\left( x \right) – {{\left( {x – 1} \right)}^2}} \right|\) có tối đa bao nhiêu điểm cực trị ?

A
\(7\).
B
\(11\).
C
\(9\).
D
\(8\).

Đặt \(h\left( x \right) = 2f\left( x \right) – {\left( {x – 1} \right)^2} \Rightarrow h'\left( x \right) = 2f'\left( x \right) – 2\left( {x – 1} \right)\). Ta vẽ thêm đường thẳng \(y = x – 1\).
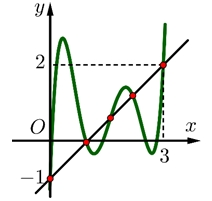
Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Ta có \(h'\left( x \right) = 0\)\( \Leftrightarrow f'\left( x \right) = x – 1\) : phương trình có \(5\) nghiệm bội lẻ.
Lập bảng biến thiên của hàm số \(h\left( x \right)\).
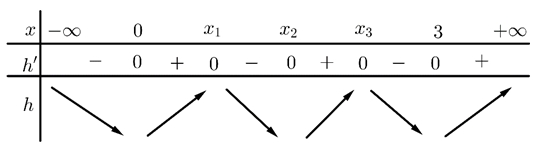
Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Đồ thị hàm số \(g\left( x \right)\) có nhiều điểm cực trị nhất khi \(h\left( x \right)\) có nhiều giao điểm với trục hoành nhất, vậy đồ thị hàm số \(h\left( x \right)\) cắt trục hoành tại nhiều nhất 6 điểm, suy ra đồ thị hàm số \(g\left( x \right)\) có tối đa \(11\) điểm cực trị.

Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Đề Kiểm Tra: Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Giải thích & Đáp án chi tiết