Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-luyen-thi-tn-thpt-nam-2023-mon-toan-online-de-10
Đề Kiểm Tra: Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10
3.
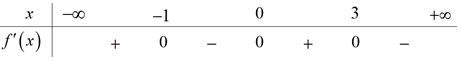 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?\(\left( { - 1;0} \right)\).
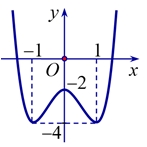
\(x = 1\).
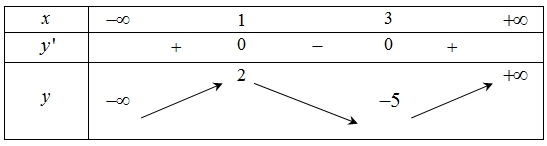 Số điểm cực trị của hàm số đã cho là
Số điểm cực trị của hàm số đã cho là\(1\).
\(y = 1\).
\(\left( {1; + \infty } \right)\).
\(\left( {2; + \infty } \right)\).
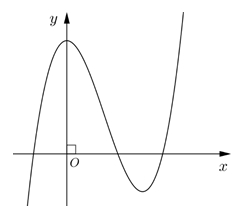
\(y = {x^3} - 3{x^2} + 3\).
\(x = 2\).
\(x = 6\).
\(\left( { - \infty ;3} \right)\).
\(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx - \int\limits_a^b {g\left( x \right)dx} } .\)
\(\int {f\left( x \right)dx} = \frac{{{x^2}}}{2} + \sin x +C.\)
\(7.\)
\(V = \int\limits_a^b {\left| {f(x)} \right|.dx} \)
Phần thực bằng \( - 5\) và Phần ảo bằng \(3i\).
\(w = - 3 - 3i.\)
\(\left| {{z_1} + {z_2}} \right| = \sqrt {13} .\)
\(\left\{ {3;4} \right\}.\)
\(6{a^3}\).
\({S_{xq}} = \pi rl\).
\(V = 32\pi \,\left( {{m^3}} \right)\).
\(\left( {2;\, - 3;\,5} \right)\).
\(\overrightarrow {{n_2}} = ( - 1; - 2;3)\).
\(\frac{{59}}{{5236}}\).
\(45^\circ \).
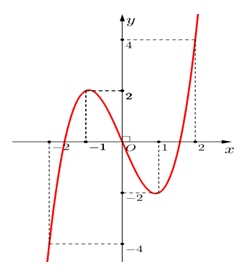
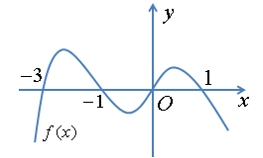
Hàm số \(f(x)\) đồng biến trên khoảng nào dưới đây?
\(\left( { - 2;0} \right)\)
\({y_{CĐ}} = - 1\).
\(x = 4\)
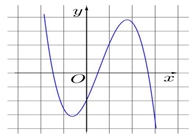
\(a < 0,b > 0,c > 0,d < 0\)..
\(y' = {2^x}\)
\(x > 11.\)
\(11.\)
\(3 - 4i.\)
\(1.\)
\(72\,c{m^3}.\)
\(I(1;0;4).\)
\(I\left( { - 1;2; - 4} \right),R = 2\sqrt 5 \).
\(\,\frac{x}{1} + \frac{y}{{ - 2}} + \frac{z}{3} = 1.\)
\(\frac{a}{2}.\)
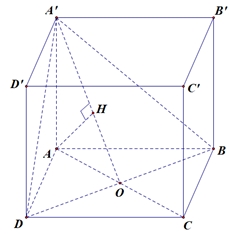 Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Gọi \(O\) là giao điểm của \(AC\) và \(BD\).Ta có
\(\left\{ \begin{array}{l}
BD \bot AO\\
BD \bot AA’
\end{array} \right. \Rightarrow BD \bot \left( {AOA’} \right) \Rightarrow A’O \bot BD\).
Khi đó
\(\left\{ \begin{array}{l}
\left( {AOA’} \right) \bot \left( {A’BD} \right)\\
\left( {AOA’} \right) \cap \left( {A’BD} \right) = A’O\\
Trong\,\left( {AOA’} \right):AH \bot A’O
\end{array} \right.\).
\(27.\)
\(4 + 4\sqrt {13} \).
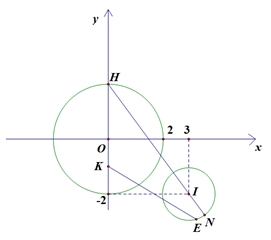 Gọi \(M\left( {x;\,y} \right)\) là điểm biểu diễn của số phức \(z = x + iy\,\left( {x,y \in \mathbb{R}} \right)\), \(E\) là điểm biểu diễn của số phức \(w\). Từ giả thiết suy ra \(M\) thuộc đường tròn tâm \(O\left( {0;\,0} \right)\), bán kính \({R_1} = 2\); \(E\) thuộc đường tròn tâm \(I\left( {3;\, – 2} \right)\), bán kính \({R_2} = 1\);Ta có\(\begin{gathered} P = \left| {{z^2} – 2zw – 4} \right| = \left| {{z^2} – 2zw – {{\left| z \right|}^2}} \right| = \left| {{z^2} – 2zw – z.\overline z } \right| = \left| z \right|.\left| {z – 2w – \overline z } \right| \hfill \\ \,\,\,\,\, = 2.\left| {z – 2w – \overline z } \right| = 2.\left| {2y – 2w} \right| = 4\left| {y – w} \right| = 4KE \geqslant HN \hfill \\ \end{gathered} \)\( \Rightarrow P \geqslant 4\left( {HI + {R_2}} \right) \Leftrightarrow P \geqslant 24\)Trong đó \(K\left( {0;\,y} \right)\), \( – 2 \leqslant y \leqslant 2\), \(H\left( {0;\,2} \right),\,N\) là giao điểm của đường tròn \(\left( I \right)\) và đường thẳng \(IH\), \({x_N} > 3\).
Gọi \(M\left( {x;\,y} \right)\) là điểm biểu diễn của số phức \(z = x + iy\,\left( {x,y \in \mathbb{R}} \right)\), \(E\) là điểm biểu diễn của số phức \(w\). Từ giả thiết suy ra \(M\) thuộc đường tròn tâm \(O\left( {0;\,0} \right)\), bán kính \({R_1} = 2\); \(E\) thuộc đường tròn tâm \(I\left( {3;\, – 2} \right)\), bán kính \({R_2} = 1\);Ta có\(\begin{gathered} P = \left| {{z^2} – 2zw – 4} \right| = \left| {{z^2} – 2zw – {{\left| z \right|}^2}} \right| = \left| {{z^2} – 2zw – z.\overline z } \right| = \left| z \right|.\left| {z – 2w – \overline z } \right| \hfill \\ \,\,\,\,\, = 2.\left| {z – 2w – \overline z } \right| = 2.\left| {2y – 2w} \right| = 4\left| {y – w} \right| = 4KE \geqslant HN \hfill \\ \end{gathered} \)\( \Rightarrow P \geqslant 4\left( {HI + {R_2}} \right) \Leftrightarrow P \geqslant 24\)Trong đó \(K\left( {0;\,y} \right)\), \( – 2 \leqslant y \leqslant 2\), \(H\left( {0;\,2} \right),\,N\) là giao điểm của đường tròn \(\left( I \right)\) và đường thẳng \(IH\), \({x_N} > 3\).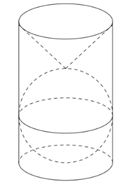
\(\frac{5}{9}\).
\(x + 2y + 2z + 3 = 0\)
\(7.\)
\(125.\)
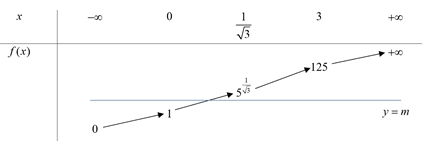 Dựa vào bảng biến thiên, để phương trình có hai nghiệm phân biệt thì\(\left[ \begin{gathered} m = 1 \hfill \\ {5^{\frac{1}{{\sqrt 3 }}}} \leqslant m < 125 \hfill \\ \end{gathered} \right.\), \(m \in {\mathbb{Z}_ + }\) \( \Rightarrow \left[ \begin{gathered} 0 < m \leqslant 1 \hfill \\ 3 \leqslant m \leqslant 124 \hfill \\ \end{gathered} \right.\). Nên có 123 giá trị m thoả mãn.
Dựa vào bảng biến thiên, để phương trình có hai nghiệm phân biệt thì\(\left[ \begin{gathered} m = 1 \hfill \\ {5^{\frac{1}{{\sqrt 3 }}}} \leqslant m < 125 \hfill \\ \end{gathered} \right.\), \(m \in {\mathbb{Z}_ + }\) \( \Rightarrow \left[ \begin{gathered} 0 < m \leqslant 1 \hfill \\ 3 \leqslant m \leqslant 124 \hfill \\ \end{gathered} \right.\). Nên có 123 giá trị m thoả mãn.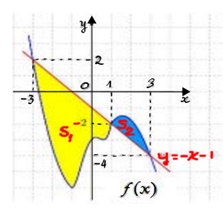
\(M - m + 6\).
\(\frac{{\sqrt 2 + 1}}{9}\).
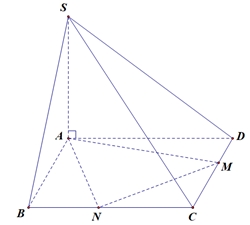 Đặt \(\widehat {BAN} = \alpha \) suy ra \(\widehat {MAD} = 45^\circ – \alpha \).Khi đó \(AN = \frac{{AB}}{{\cos \alpha }} = \frac{1}{{\cos \alpha }}\) và \(AM = \frac{{AD}}{{\cos \left( {45^\circ – \alpha } \right)}} = \frac{1}{{\cos \left( {45^\circ – \alpha } \right)}}\).Do đó diện tích tam giác \(AMN\) bằng \({B_{AMN}} = \frac{1}{2}AM.AN.\sin 45^\circ = \frac{{\sqrt 2 }}{4}.\frac{1}{{\cos \alpha .\cos \left( {45^\circ – \alpha } \right)}}\).Thể tích \(S.AMN\) bằng \({V_{S.AMN}} = \frac{1}{3}{B_{AMN}}.SA = \frac{{\sqrt 2 }}{{12}}.\frac{1}{{\cos \alpha .\cos \left( {45^\circ – \alpha } \right)}}\).Thể tích của khối chóp \(S.AMN\) nhỏ nhất khi \(\cos \alpha .\cos \left( {45^\circ – \alpha } \right)\) lớn nhất.Xét \(f\left( \alpha \right) = \cos \alpha .\cos \left( {45^\circ – \alpha } \right)\) trong đó \(\alpha \in \left( {0^\circ ;45^\circ } \right)\).Ta có \(f'\left( \alpha \right) = \sin \left( {45^\circ – 2\alpha } \right)\); \(f'\left( \alpha \right) = 0 \Leftrightarrow \alpha = \frac{{45^\circ }}{2}\).Bảng biến thiên
Đặt \(\widehat {BAN} = \alpha \) suy ra \(\widehat {MAD} = 45^\circ – \alpha \).Khi đó \(AN = \frac{{AB}}{{\cos \alpha }} = \frac{1}{{\cos \alpha }}\) và \(AM = \frac{{AD}}{{\cos \left( {45^\circ – \alpha } \right)}} = \frac{1}{{\cos \left( {45^\circ – \alpha } \right)}}\).Do đó diện tích tam giác \(AMN\) bằng \({B_{AMN}} = \frac{1}{2}AM.AN.\sin 45^\circ = \frac{{\sqrt 2 }}{4}.\frac{1}{{\cos \alpha .\cos \left( {45^\circ – \alpha } \right)}}\).Thể tích \(S.AMN\) bằng \({V_{S.AMN}} = \frac{1}{3}{B_{AMN}}.SA = \frac{{\sqrt 2 }}{{12}}.\frac{1}{{\cos \alpha .\cos \left( {45^\circ – \alpha } \right)}}\).Thể tích của khối chóp \(S.AMN\) nhỏ nhất khi \(\cos \alpha .\cos \left( {45^\circ – \alpha } \right)\) lớn nhất.Xét \(f\left( \alpha \right) = \cos \alpha .\cos \left( {45^\circ – \alpha } \right)\) trong đó \(\alpha \in \left( {0^\circ ;45^\circ } \right)\).Ta có \(f'\left( \alpha \right) = \sin \left( {45^\circ – 2\alpha } \right)\); \(f'\left( \alpha \right) = 0 \Leftrightarrow \alpha = \frac{{45^\circ }}{2}\).Bảng biến thiên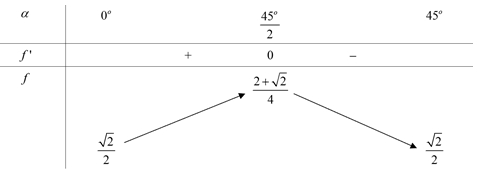 Từ bảng biến thiên ta có \(\mathop {\max }\limits_{\alpha \in \left[ {0^\circ ;45^\circ } \right]} f\left( \alpha \right) = f\left( {\frac{{45^\circ }}{2}} \right) = \frac{{2 + \sqrt 2 }}{4}\).Vậy thể tích nhỏ nhất của \(S.AMN\) bằng \({V_{S.AMN}} = \frac{{\sqrt 2 }}{{12}}.\frac{1}{{\frac{{2 + \sqrt 2 }}{4}}} = \frac{{\sqrt 2 – 1}}{3}\).
Từ bảng biến thiên ta có \(\mathop {\max }\limits_{\alpha \in \left[ {0^\circ ;45^\circ } \right]} f\left( \alpha \right) = f\left( {\frac{{45^\circ }}{2}} \right) = \frac{{2 + \sqrt 2 }}{4}\).Vậy thể tích nhỏ nhất của \(S.AMN\) bằng \({V_{S.AMN}} = \frac{{\sqrt 2 }}{{12}}.\frac{1}{{\frac{{2 + \sqrt 2 }}{4}}} = \frac{{\sqrt 2 – 1}}{3}\).\(T = \frac{{134}}{{25}}\).
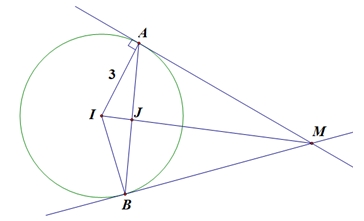 Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1; – 1;2} \right),R = 3,IM = 5\).Gọi \(A,B\) là các tiếp điểm. Khi đó các tiếp điểm của các tiếp tuyến kẻ từ \(M\) tới mặt cầu đường tròn \(\left( C \right)\) có tâm \(J\) là trung điểm của dây \(AB\).Xét \(\Delta IAM\) có \(I{A^2} = IJ.IM \Leftrightarrow I{J^2} = \frac{9}{{25}}\).Phương trình \(IM:\left\{ \begin{gathered} x = 1 \hfill \\ y = – 1 + 4t \hfill \\ z = 2 – 3t \hfill \\ \end{gathered} \right.\). Vì \(J \in IM \Rightarrow J\left( {1;4t – 1;2 – 3t} \right),t \in \mathbb{R}\).Ta có: \(I{J^2} = \frac{9}{{25}} \Leftrightarrow {\left( {4t} \right)^2} + {\left( { – 3t} \right)^2} = \frac{{81}}{{25}} \Leftrightarrow {t^2} = \frac{{81}}{{{{25}^2}}} \Rightarrow \left[ \begin{gathered} t = \frac{9}{{25}} \hfill \\ t = – \frac{9}{{25}} \hfill \\ \end{gathered} \right.\).+) Với \(t = \frac{9}{{25}} \Rightarrow J\left( {1;\frac{{11}}{{25}};\frac{{23}}{{25}}} \right) \Rightarrow T = 2a + b + c = \frac{{84}}{{25}}\).+) Với \(t = – \frac{9}{{25}} \Rightarrow J\left( {1;\frac{{ – 61}}{{25}};\frac{{77}}{{25}}} \right) \Rightarrow T = 2a + b + c = \frac{{66}}{{25}}\). (loại)
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1; – 1;2} \right),R = 3,IM = 5\).Gọi \(A,B\) là các tiếp điểm. Khi đó các tiếp điểm của các tiếp tuyến kẻ từ \(M\) tới mặt cầu đường tròn \(\left( C \right)\) có tâm \(J\) là trung điểm của dây \(AB\).Xét \(\Delta IAM\) có \(I{A^2} = IJ.IM \Leftrightarrow I{J^2} = \frac{9}{{25}}\).Phương trình \(IM:\left\{ \begin{gathered} x = 1 \hfill \\ y = – 1 + 4t \hfill \\ z = 2 – 3t \hfill \\ \end{gathered} \right.\). Vì \(J \in IM \Rightarrow J\left( {1;4t – 1;2 – 3t} \right),t \in \mathbb{R}\).Ta có: \(I{J^2} = \frac{9}{{25}} \Leftrightarrow {\left( {4t} \right)^2} + {\left( { – 3t} \right)^2} = \frac{{81}}{{25}} \Leftrightarrow {t^2} = \frac{{81}}{{{{25}^2}}} \Rightarrow \left[ \begin{gathered} t = \frac{9}{{25}} \hfill \\ t = – \frac{9}{{25}} \hfill \\ \end{gathered} \right.\).+) Với \(t = \frac{9}{{25}} \Rightarrow J\left( {1;\frac{{11}}{{25}};\frac{{23}}{{25}}} \right) \Rightarrow T = 2a + b + c = \frac{{84}}{{25}}\).+) Với \(t = – \frac{9}{{25}} \Rightarrow J\left( {1;\frac{{ – 61}}{{25}};\frac{{77}}{{25}}} \right) \Rightarrow T = 2a + b + c = \frac{{66}}{{25}}\). (loại)\(C_n^5 = \frac{{n!}}{{5!(n - 5)!}}\).
