Đề Luyện Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 9
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-luyen-thi-tot-nghiep-thpt-nam-2023-mon-toan-online-de-9
Đề Kiểm Tra: Đề Luyện Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 9
\(1 - 2i\).
\(I\left( {1; - 2;3} \right);R = 3\).
Điểm \(N(0; - 2)\).
\(\sqrt 2 a\).
\( - \frac{1}{2}\cos 2x + C\).
\(3\).
\(T = \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)\)
\(\frac{{{a^3}\sqrt 3 }}{6}\).
\(D = \mathbb{R}\backslash \left\{ { \pm 1} \right\}\).
\(x = 68\).
\(I = 4\).
\(w = - 4 - 2i\).
\(\overrightarrow n = \left( { - 2;3;4} \right)\).
\(\overrightarrow x = \left( { - 2;\,\, - 1;\,\,19} \right)\)
\( - 5\).
\(1\)
\(3 - {\log _3}a\)
\(y = {x^3} - 3x + 2\).
\({\vec u_3} = ( - 1;2;1)\).
75.
\(\frac{{\sqrt 6 {a^3}}}{3}\).
\(y' = - {17^{ - x}}\ln 17\).
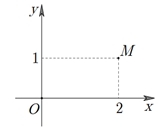
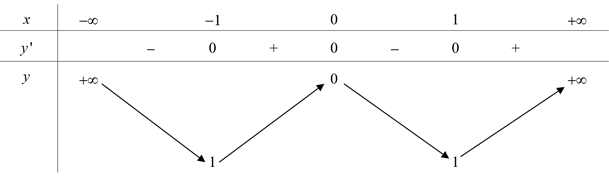 Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?\(\left( {0;1} \right)\).
\(\pi {a^2}\).
\(I = \frac{5}{8}\).
\(12\)
\(\frac{{{x^3}}}{3} - {3^x} + \frac{1}{{{x^2}}} + C,C \in R\)
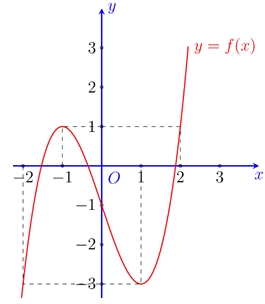
\(y = - 3\).
\(x = 2\).
\(y = x\sqrt {{x^2} + 1} \).
\(3\).
\(60^\circ \).
\(1\).
\(x - 2y + z + 4 = 0\).
\(\frac{{\text{2}}}{{\text{5}}}\).
\(\frac{{2a\sqrt {21} }}{7}\).
\(\frac{{41}}{{126}}\).
\(\left\{ \begin{gathered} x = 1 + 2t \hfill \\ y = - 2 - t \hfill \\ z = 3 + 3t \hfill \\ \end{gathered} \right.\).
4.
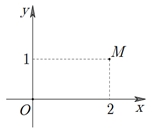
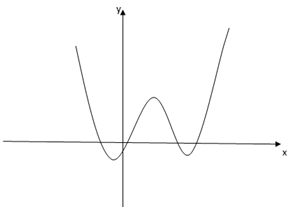 Số giao điểm của đồ thị hàm số \(y = {\left[ {f'\left( x \right)} \right]^2} – f''\left( x \right).f\left( x \right)\) và trục \(Ox\) là:
Số giao điểm của đồ thị hàm số \(y = {\left[ {f'\left( x \right)} \right]^2} – f''\left( x \right).f\left( x \right)\) và trục \(Ox\) là:\(4\).
\( - \frac{{104}}{{225}}\).
\(\frac{{{a^3}\sqrt 6 }}{{12}}\).
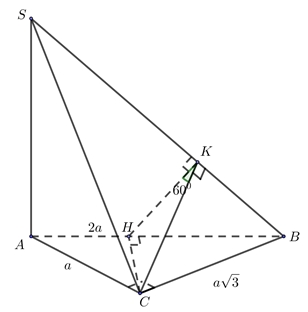 Trong \(\Delta ABC\) kẻ \(CH \bot AB\)\( \Rightarrow CH \bot \left( {SAB} \right)\) \( \Rightarrow CH \bot SB{\kern 1pt} \left( 1 \right)\).\(BC = \sqrt {A{B^2} – A{C^2}} = a\sqrt 3 \),\(BH.BA = B{C^2}\),\( \Rightarrow BH = \frac{{3a}}{2}\), \(CH = \sqrt {B{C^2} – B{H^2}} = \frac{{a\sqrt 3 }}{2}\).Trong \(\Delta SAB\)kẻ \(HK \bot SB\) \( \Rightarrow CK \bot SB{\kern 1pt} \left( 2 \right)\).Từ \(\left( 1 \right),\left( 2 \right)\) \( \Rightarrow HK \bot SB\).Góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBC} \right)\) là \(\widehat {CKH} = 60^\circ \).Trong vuông \(\Delta CKH\) có \(HK = CH.\cot 60^\circ = \frac{a}{2}\), \(BK = \sqrt {B{H^2} – H{K^2}} = a\sqrt 2 \). nên \(\frac{{SA}}{{HK}} = \frac{{AB}}{{BK}} = \frac{{2a}}{{a\sqrt 2 }}\)\( \Rightarrow SA = \frac{a}{{\sqrt 2 }}\)
Trong \(\Delta ABC\) kẻ \(CH \bot AB\)\( \Rightarrow CH \bot \left( {SAB} \right)\) \( \Rightarrow CH \bot SB{\kern 1pt} \left( 1 \right)\).\(BC = \sqrt {A{B^2} – A{C^2}} = a\sqrt 3 \),\(BH.BA = B{C^2}\),\( \Rightarrow BH = \frac{{3a}}{2}\), \(CH = \sqrt {B{C^2} – B{H^2}} = \frac{{a\sqrt 3 }}{2}\).Trong \(\Delta SAB\)kẻ \(HK \bot SB\) \( \Rightarrow CK \bot SB{\kern 1pt} \left( 2 \right)\).Từ \(\left( 1 \right),\left( 2 \right)\) \( \Rightarrow HK \bot SB\).Góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBC} \right)\) là \(\widehat {CKH} = 60^\circ \).Trong vuông \(\Delta CKH\) có \(HK = CH.\cot 60^\circ = \frac{a}{2}\), \(BK = \sqrt {B{H^2} – H{K^2}} = a\sqrt 2 \). nên \(\frac{{SA}}{{HK}} = \frac{{AB}}{{BK}} = \frac{{2a}}{{a\sqrt 2 }}\)\( \Rightarrow SA = \frac{a}{{\sqrt 2 }}\)Thể tích hình chóp \(S.ABC\) là \(V = \frac{1}{3}SA.{S_{\Delta ABC}}\)\( = \frac{1}{3}\frac{a}{{\sqrt 2 }}.\frac{1}{2}.a.\sqrt 3 .a = \frac{{{a^3}\sqrt 6 }}{{12}}\).
\(2.\)
\(\frac{{x - 3}}{1} = \frac{{y + 2}}{{ - 1}} = \frac{{z + 3}}{{ - 2}}\).
\(\frac{{\sqrt 2 }}{2}\).
\(\frac{{16}}{3}\).
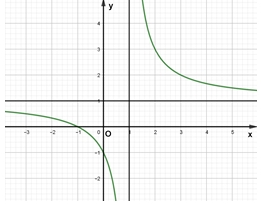
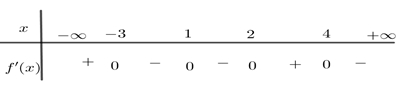 Bất phương trình \({3^{f\left( x \right) + m}} \leqslant 4f\left( x \right) + 1 + 4m\) nghiệm đúng với mọi số thực \(x \in \left( { – 2\,;\,2} \right)\) khi và chỉ khi
Bất phương trình \({3^{f\left( x \right) + m}} \leqslant 4f\left( x \right) + 1 + 4m\) nghiệm đúng với mọi số thực \(x \in \left( { – 2\,;\,2} \right)\) khi và chỉ khi\(m \in \left( { - 2\,;\, - 1} \right)\).
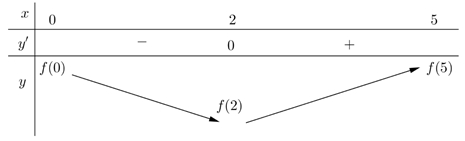 Suy ra \({\min _{\left[ {0\,;\,5} \right]}} = f\left( x \right) = f\left( 2 \right).\,\) Và \({\max _{\left[ {0\,;\,5} \right]}}f\left( x \right) = \max \left\{ {f\left( 0 \right),f\left( 5 \right)} \right\}\).Ta có \(f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right) \Leftrightarrow f\left( 5 \right) – f\left( 0 \right) = f\left( 3 \right) – f\left( 2 \right)\).Vì \(f\left( x \right)\) đồng biến trên đoạn \(\left[ {2\,;\,5} \right]\) nên \(f\left( 3 \right) > f\left( 2 \right) \Rightarrow f\left( 5 \right) – f\left( 0 \right) > 0 \Rightarrow f\left( 5 \right) > f\left( 0 \right)\).Vậy \({\max _{\left[ {0\,;\,5} \right]}}f\left( x \right) = \max \left\{ {f\left( 0 \right),\,f\left( 5 \right)} \right\} = f\left( 5 \right)\).
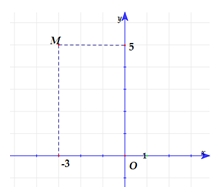
Suy ra \({\min _{\left[ {0\,;\,5} \right]}} = f\left( x \right) = f\left( 2 \right).\,\) Và \({\max _{\left[ {0\,;\,5} \right]}}f\left( x \right) = \max \left\{ {f\left( 0 \right),f\left( 5 \right)} \right\}\).Ta có \(f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right) \Leftrightarrow f\left( 5 \right) – f\left( 0 \right) = f\left( 3 \right) – f\left( 2 \right)\).Vì \(f\left( x \right)\) đồng biến trên đoạn \(\left[ {2\,;\,5} \right]\) nên \(f\left( 3 \right) > f\left( 2 \right) \Rightarrow f\left( 5 \right) – f\left( 0 \right) > 0 \Rightarrow f\left( 5 \right) > f\left( 0 \right)\).Vậy \({\max _{\left[ {0\,;\,5} \right]}}f\left( x \right) = \max \left\{ {f\left( 0 \right),\,f\left( 5 \right)} \right\} = f\left( 5 \right)\).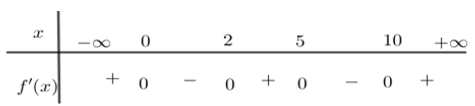 Biết rằng \(f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right)\). Giá trị nhỏ nhất, giá trị lớn nhất của hàm \(y = f\left( x \right)\) trên đoạn \(\left[ {0\,;\,5} \right]\) lần lượt là
Biết rằng \(f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right)\). Giá trị nhỏ nhất, giá trị lớn nhất của hàm \(y = f\left( x \right)\) trên đoạn \(\left[ {0\,;\,5} \right]\) lần lượt là\(f\left( 0 \right)\,,\,f\left( 5 \right)\).
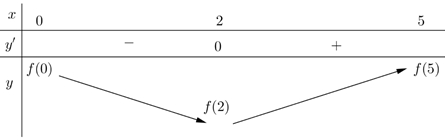 Suy ra \({\min _{\left[ {0\,;\,5} \right]}} = f\left( x \right) = f\left( 2 \right).\,\) Và \({\max _{\left[ {0\,;\,5} \right]}}f\left( x \right) = \max \left\{ {f\left( 0 \right),f\left( 5 \right)} \right\}\).Ta có \(f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right) \Leftrightarrow f\left( 5 \right) – f\left( 0 \right) = f\left( 3 \right) – f\left( 2 \right)\).Vì \(f\left( x \right)\) đồng biến trên đoạn \(\left[ {2\,;\,5} \right]\) nên \(f\left( 3 \right) > f\left( 2 \right) \Rightarrow f\left( 5 \right) – f\left( 0 \right) > 0 \Rightarrow f\left( 5 \right) > f\left( 0 \right)\).Vậy \({\max _{\left[ {0\,;\,5} \right]}}f\left( x \right) = \max \left\{ {f\left( 0 \right),\,f\left( 5 \right)} \right\} = f\left( 5 \right)\).
Suy ra \({\min _{\left[ {0\,;\,5} \right]}} = f\left( x \right) = f\left( 2 \right).\,\) Và \({\max _{\left[ {0\,;\,5} \right]}}f\left( x \right) = \max \left\{ {f\left( 0 \right),f\left( 5 \right)} \right\}\).Ta có \(f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right) \Leftrightarrow f\left( 5 \right) – f\left( 0 \right) = f\left( 3 \right) – f\left( 2 \right)\).Vì \(f\left( x \right)\) đồng biến trên đoạn \(\left[ {2\,;\,5} \right]\) nên \(f\left( 3 \right) > f\left( 2 \right) \Rightarrow f\left( 5 \right) – f\left( 0 \right) > 0 \Rightarrow f\left( 5 \right) > f\left( 0 \right)\).Vậy \({\max _{\left[ {0\,;\,5} \right]}}f\left( x \right) = \max \left\{ {f\left( 0 \right),\,f\left( 5 \right)} \right\} = f\left( 5 \right)\).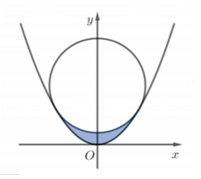
\(\frac{{2\pi + 3\sqrt 3 - 8}}{{12}}\).
\(1\)
