Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Online Môn Toán-Đề 4
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-thi-thu-tot-nghiep-thpt-nam-2023-online-mon-toan-de-4
Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Online Môn Toán-Đề 4
\(\frac{{11}}{5} - \frac{2}{5}i.\)
\(\sqrt 7 \).
\(K\left( {0;\,0;\,1} \right)\).
\(S = 36\pi \,c{m^3}\).
\(\int f (x)dx = - \frac{3}{2}{x^{ - \frac{2}{3}}} + C\).
\(0\).
\(\left( { - \infty ; - 32} \right)\).
\( V=2{a^3}\sqrt 3 \).
\(\mathbb{R}\).
\(x = 3\).
\(11\).
\( - \frac{1}{2}i\).
\(\overrightarrow {{u_4}} = \left( {2\,;3\,;3} \right)\).
\(m = 1\).
\( - \frac{2}{5}\).
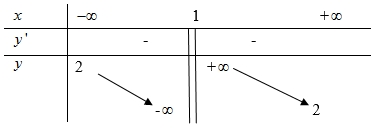 Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho lần lượt là
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho lần lượt là\(x = 2,\,y = 1\).
\(\frac{2}{{1011}}\).
\(y = \frac{{x - 1}}{{x + 1}}\).
Điểm \(P\left( {2;1;1} \right)\).
\({5^5}\).
\(80\).
\(y' = \left( {2x + 1} \right){e^{{x^2} + x}}\).
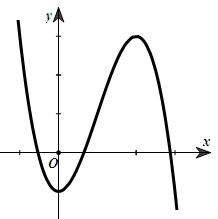
Hàm số \(f\left( x \right)\) đồng biến trên \(\left( {1; + \infty } \right)\).
\(50\pi \).
\(I = \frac{{11}}{2}\).
\(31\).
\(f\left( x \right) = 2 + 2\cos 2x\).

\( - 1\).
\(x = 2\).
\(y = \frac{{x + 4}}{{x + 1}}\).
\({a^5}{b^4}\).
\(60^\circ \).
\(1\).
\(2x - 5y + z - 17 = 0\).
\( - 1 - i\).
\(\frac{{3a\sqrt 2 }}{2}\).
\(\frac{{35}}{{44}}\) .
\(\frac{x}{2} = \frac{{y + 1}}{1} = \frac{{z - 3}}{1}\).
\(0\).
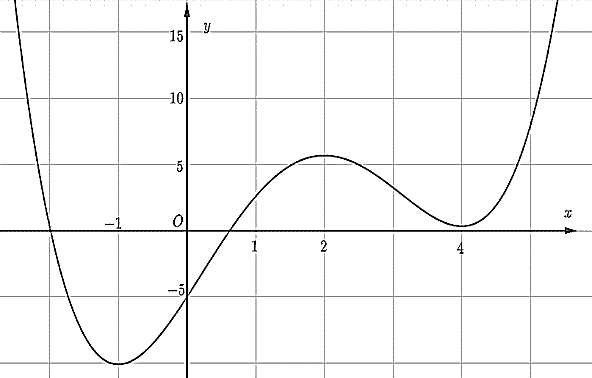 Số nghiệm thực phân biệt của phương trình \({\log _{\sqrt 2 }}(x – 1).f'(f(x)) = 0\) là
Số nghiệm thực phân biệt của phương trình \({\log _{\sqrt 2 }}(x – 1).f'(f(x)) = 0\) là\(9\).
Theo đồ thị ta có:
-Phương trình (a) có 2 nghiệm thực phân biệt bé hơn 1;
-Phương trình (b) có 4 nghiệm thực phân biệt \({x_1} < {x_2} < 1 < {x_3} < 4 < {x_4}\);
-Phương trình (c) có 4 nghiệm thực phân biệt \({x_5} < 1 < {x_6} < {x_7} < 4 < {x_8}\)
Do đó, phương trình \({\log _{\sqrt 2 }}(x - 1).f'(f(x)) = 0\) có 6 nghiệm thực phân biệt là \(2;{x_3};{x_4};{x_6};{x_7};{x_8}.\)
\( - 1\).
Với \(f\left( 0 \right) = – 2 \Rightarrow – 2.\cos 2.0 + \sin 0 + C = – 2 \Rightarrow C = 0\)
Vậy \(f\left( x \right) = – 2\cos 2x + \sin x\)
Ta có \(F\left( x \right) = \int {f\left( x \right)dx = } \int {\left( { – 2\cos 2x + \sin x} \right)} dx = – \sin 2x – \cos x + C'\)
Với \(F\left( \pi \right) = 3 \Rightarrow – \sin 2\pi – \cos \pi + C' = 3 \Rightarrow C' = 2\)
Vậy \(F\left( x \right) = – \sin 2x – \cos x + 2\)
khi đó \(F\left( {\frac{\pi }{2}} \right) = – \sin \pi – \cos \frac{\pi }{2} + 2 = 2\).
\(\frac{{32}}{3}{a^3}\).
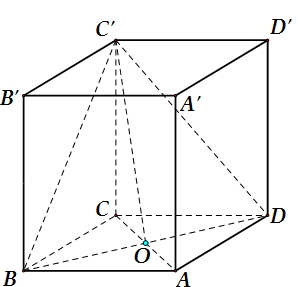
Gọi \(O\) là tâm của hình vuông \(ABCD\). Dễ thấy \(AC \bot BD\) tại \(O\) và \(BD \bot CC'\)
Suy ra \(BD \bot \left( {ACC'A'} \right)\) \( \Rightarrow BD \bot OC'\).
Suy ra \(\widehat {\left[ {\left( {C'BD} \right),\left( {ABCD} \right)} \right]} = \widehat {\left( {OC',OC} \right)} = {45^0}\).
Suy ra \(CC' = OC = \frac{{AC}}{2} = a\sqrt 2 \).
Vậy, \({V_{ABCD.A'B'C'D'}} = CC'.{\left( {\frac{{AC}}{{\sqrt 2 }}} \right)^2} = a\sqrt 2 .4{a^2} = 4\sqrt 2 {a^3}\).
\(4\).
Phương trình có nghiệm thực \(z\),
khi đó: \(\left| z \right| = \,5 \Leftrightarrow z = \pm 5\)
Phương trình có nghiệm \(z = 5\) hoặc \(z = – 5\)\( \Leftrightarrow \left[ \begin{gathered} 25 – 30 + 1 – m = 0 \hfill \\ 25 + 30 + 1 – m = 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m = – 4 \hfill \\ m = 56 \hfill \\ \end{gathered} \right.\) (thỏa mãn).
+ TH2: \(\Delta ' < 0 \Leftrightarrow m + 8 < 0 \Leftrightarrow m < - 8\).Khi đó phương trình có nghiệm phức \(z = 3 \pm i.\sqrt { - \left( {m + 8} \right)} \)
Ta có: \(\left| z \right| = \,5 \Leftrightarrow 9 - \left( {m + 8} \right) = 25 \Leftrightarrow m = - 24\) (thỏa mãn).
Vậy có 3 giá trị của \(m\).
\(2\sqrt {15} \).
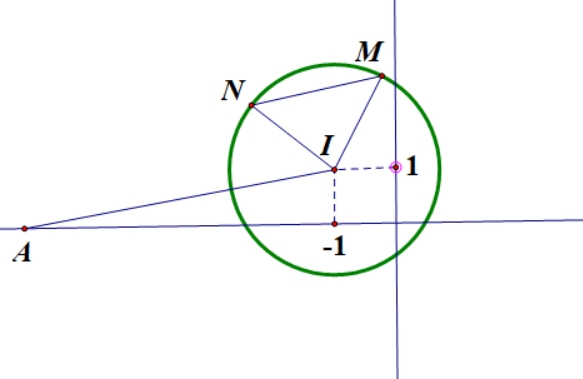
Có \({\text{w}} = \frac{{z + 2}}{{z – 2i}} = \frac{{a + 2 + bi}}{{a + \left( {b – 2} \right)i}}\) \( = \frac{{\left( {a + 2 + bi} \right)\left[ {a – \left( {b – 2} \right)i} \right]}}{{{a^2} + {{\left( {b – 2} \right)}^2}}}\)\( = \frac{{a\left( {a + 2} \right) + b\left( {b – 2} \right) + \left[ { – \left( {a + 2} \right)\left( {b – 2} \right) + ab} \right]i}}{{{a^2} + {{\left( {b – 2} \right)}^2}}}\)\({\text{w}}\) là số thuần ảo \( \Leftrightarrow \left\{ \begin{gathered} a\left( {a + 2} \right) + b\left( {b – 2} \right) = 0\,\,\,\left( 1 \right) \hfill \\ {a^2} + {\left( {b – 2} \right)^2} \ne 0 \hfill \\ \end{gathered} \right.\)Có \(\left( 1 \right) \Leftrightarrow {a^2} + {b^2} + 2a – 2b = 0\).
Suy ra \(M\) thuộc đường tròn \(\left( C \right)\) tâm \(I\left( { – 1;1} \right)\), bán kính \(R = \sqrt 2 \).\({z_1},{z_2} \in S\) được biểu điễn bởi \(M,N\) nên \(M,N\) thuộc đường tròn \(\left( C \right)\) và \(\left| {{z_1} – {z_2}} \right| = MN = \sqrt 3 \). Gọi \(A\left( { – 6;0} \right)\)
\(\frac{{16}}{{15}}\)
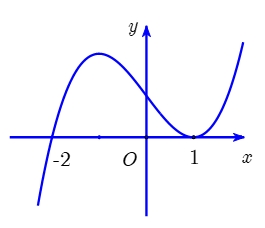
Suy ra \(f\left( x \right) – g(x) = {\left( {x – 1} \right)^2}{\left( {x + 1} \right)^2}\)
\(S = \int\limits_ – ^1 {\left| {f\left( x \right) – g\left( x \right)} \right|dx} = \int\limits_{ – 2}^1 {{{\left( {{x^2} – 1} \right)}^2}dx = } \frac{{16}}{{15}}\)
\(\left\{ \begin{gathered} x = 1 + t \hfill \\ y = 4 + 2t \hfill \\ z = 1 + 3t \hfill \\ \end{gathered} \right.\).
Giả sử \(M\) là giao điểm của \(\Delta \) với trục \(Oy\)\( \Rightarrow \,M\left( {0;b;0} \right).\)
Khi đó, \(\Delta \) có một vectơ chỉ phương là \(\overrightarrow {AM} \left( {1;b\, – 2;\,3} \right)\)
Do \(\Delta //\left( P \right)\) nên \(\overrightarrow {AM} .\overrightarrow n = 0 \Leftrightarrow 1 – 2b + 4 + 3 = 0 \Leftrightarrow b = 4\)
Đường thẳng cần tìm đi qua \(A\left( { – 1;2; – 3} \right)\) và có một vectơ chỉ phương \(\overrightarrow {AM} \left( {1;\,2;\,3} \right)\), nên có phương trình là:
\(\left\{ \begin{gathered} x = – 1 + t \hfill \\ y = 2 + 2t \hfill \\ z = – 3 + 3t \hfill \\ \end{gathered} \right.\)
\(18\pi {a^3}\).
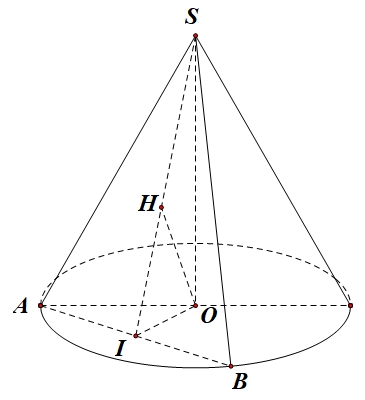
Xét hình nón đỉnh \(S\) có chiều cao \(h = SO = 2a\).Thiết diện đi qua đỉnh của hình nón là tam giác \(SAB\) cân tại \(S\).
+ Gọi \(I\) là trung điểm của đoạn thẳng \(AB\).
Trong tam giác \(SOI\), kẻ \(OH \bot SI\), \(H \in SI\).
+ \(\left\{ \begin{gathered} AB \bot OI \hfill \\ AB \bot SO \hfill \\ \end{gathered} \right. \Rightarrow AB \bot \left( {SOI} \right) \Rightarrow AB \bot OH\).
+\(\left\{ \begin{gathered} OH \bot SI \hfill \\ OH \bot AB \hfill \\ \end{gathered} \right.\)
\( \Rightarrow OH \bot \left( {SAB} \right)\)\( \Rightarrow d\left( {O\,,\,\left( {SAB} \right)} \right) = OH = \frac{{3a}}{2}\).
Xét tam giác \(SOI\)vuông tại \(O\), ta có \(\frac{1}{{O{I^2}}} = \frac{1}{{O{H^2}}} – \frac{1}{{S{O^2}}} = \frac{4}{{9{a^2}}} – \frac{1}{{4{a^2}}} = \frac{7}{{36{a^2}}}\) \( \Rightarrow OI = \frac{{6a}}{{\sqrt 7 }}\).và \(SI = \sqrt {O{I^2} + S{O^2}} = \sqrt {{{\left( {\frac{{6a}}{{\sqrt 7 }}} \right)}^2}+ {{\left( {2a} \right)}^2}} = \frac{{8a\sqrt 7 }}{7}\).
Ta có \({S_{\Delta SAB}} = \frac{{24{a^2}\sqrt 3 }}{7} \Leftrightarrow \frac{1}{2}SI.AB = \frac{{24{a^2}\sqrt 3 }}{7} \Rightarrow AB = \frac{{6a\sqrt {21} }}{7} \Rightarrow IA = \frac{{AB}}{2} = \frac{{3a\sqrt {21} }}{7}\)
Xét tam giác \(IAO\)vuông tại \(I \Rightarrow R = OA = \sqrt {O{I^2} + I{A^2}} = \sqrt {{{\left( {\frac{{6a}}{{\sqrt 7 }}} \right)}^2} + {{\left( {\frac{{3a\sqrt {21} }}{7}} \right)}^2}} = 3a\).
Thể tích của khối nón giới hạn bởi hình nón là: \(V = \frac{1}{3}h.\pi {R^2} = \frac{1}{3}.2a.\pi .{\left( {3a} \right)^2} = 6\pi {a^3}.\)
\(4\).
Đặt \(f\left( b \right) = \frac{1}{{{3^a}}}{\left( {\frac{3}{4}} \right)^b} + 65{\left( {\frac{1}{4}} \right)^b} – {4^{{a^2}}}\), với \(b \in \left[ { – 11;11} \right]\).
Ta có\(f'\left( b \right) = \frac{1}{{{3^a}}}{\left( {\frac{3}{4}} \right)^b}\ln \frac{3}{4} + 65{\left( {\frac{1}{4}} \right)^b}\ln \frac{1}{4} < 0,\forall b \in \left[ { - 11;11} \right].\)
Do đó \(f\left( b \right)\) nghịch biến trên \(\left[ { - 11;11} \right]\).
Điều này dẫn đến yêu cầu bài toán trở thành \(f\left( { - 8} \right) \geqslant 0 \Leftrightarrow {4^{{a^2} - 8}} \leqslant {3^{ - a - 8}} + 65.\)
Nếu \(a \leqslant - 8\) thì \({a^2} - 8 > – a – 8 + 4\).
Suy ra\({4^{{a^2} – 8}} > {4^{ – a – 8}} \cdot {4^4} \geqslant {3^{ – a – 8}} \cdot {4^4} = {3^{ – a – 8}} + \left( {{4^4} – 1} \right){3^{ – a – 8}} > {3^{a – 8}} + 65.\)
Nếu \(a > – 8\) thì do thì \({3^{ – a – 8}} < 1\), mà \(a \in \mathbb{Z}\) nên \({4^{{a^2} - 8}} \leqslant 66 \Leftrightarrow {a^2} \leqslant 8 + {\log _4}66 \Rightarrow a \in \left\{ { - 3; - 2; - 1;0;1;2;3} \right\}.\)
Thử lại tất cả \(7\) giá trị nguyên trên đều thỏa mãn yêu cầu.
16.
Ta có: \(M \in Oy \Rightarrow M\left( {0;\,a;\,0} \right)\)Gọi \(\left( P \right)\) là mặt phẳng chứa hai tiếp tuyến từ \(M\) đến \(\left( S \right)\).
Khi đó \(\left( P \right)\) đi qua \(M\left( {0;\,a;\,0} \right)\), vuông góc với đường thẳng \(d\), phương trình mặt phẳng \(\left( P \right)\) là: \(4x – 2\left( {y – a} \right) + z = 0 \Leftrightarrow 4x – 2y + z + 2a = 0\).
Ta có điểm \(M\) thoả mãn giả thiết là điểm nằm ngoài mặt cầu, suy ra \(IM > R \Leftrightarrow {\left( { – 2} \right)^2} + {\left( {a + 3} \right)^2} + 9 > 25 \Leftrightarrow {\left( {a + 3} \right)^2} > 12\) (1)
Các mặt phẳng \(\left( P \right)\) thoả mãn giả thiết phải cắt mặt cầu nên ta có: \(d\left( {I,\left( P \right)} \right) < R \Leftrightarrow \frac{{\left| {8 + 6 + 3 + 2a} \right|}}{{\sqrt {21} }} < 5 \Leftrightarrow \left| {2a + 17} \right| < 5\sqrt {21} \) (2)
Từ (1) và (2), suy ra: \(\left\{ \begin{gathered} {\left( {a + 3} \right)^2} > 12 \hfill \\ \left| {2a + 17} \right| < 5\sqrt {21} \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {{a^2} + 6a - 3 > 0} \\ { – 14 < 2a < 1} \end{array}} \right. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} a > – 3 + 2\sqrt 3 \hfill \\ a < - 3 - 2\sqrt 3 \hfill \\ \end{gathered} \right. \hfill \\ \frac{{ - 5\sqrt {21} - 17}}{2} < a < \frac{{5\sqrt {21} - 17}}{2} \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow \left[ \begin{gathered} - 3 + 2\sqrt 3 < a < \frac{{5\sqrt {21} - 17}}{2} \hfill \\ \frac{{ - 5\sqrt {21} - 17}}{2} < a < - 3 - 2\sqrt 3 \hfill \\ \end{gathered} \right.\) do \(a \in \mathbb{Z}\) nên có \(2 + 17 = 19\) giá trị của thoả mãn.
Vậy có 19 điểm \(M\) thoả mãn.
 Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {{x^2} – 8x + m} \right)\) có \(5\) điểm cực trị
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {{x^2} – 8x + m} \right)\) có \(5\) điểm cực trị15.
Yêu cầu bài toán \( \Leftrightarrow g'\left( x \right) = 0\) có \(5\) nghiệm bội lẻ \( \Leftrightarrow \) mỗi phương trình \(\left( 1 \right),{\text{ }}\left( 2 \right)\) đều có hainghiệm phân biệt khác \(4.\) \(\left( * \right)\)
Cách 1: \(\left( * \right)\) \( \Leftrightarrow \left\{ \begin{gathered} 16 – m > 0 \hfill \\ 16 – m + 2 > 0 \hfill \\ m \ne 16 \hfill \\ m \ne 18 \hfill \\ \end{gathered} \right. \Leftrightarrow m < 16\).Vậy có \(15\) giá trị \(m\) nguyên dương thỏa mãn điều kiện.
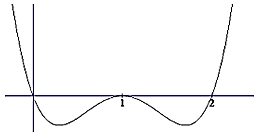
Cách 2: Xét đồ thị \(\left( C \right)\) của hàm số \(y = {x^2} - 8x\) và hai đường thẳng \({d_1}:y = - m,{\text{ }}{d_2}:y = - m + 2\) (hình vẽ).
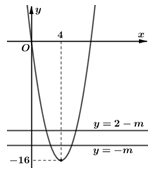 Khi đó \(\left( * \right){\text{ }} \Leftrightarrow {\text{ }}{d_1},{\text{ }}{d_2}\) cắt \(\left( C \right)\) tại bốn điểm phân biệt \( \Leftrightarrow – m > – 16 \Leftrightarrow m < 16.\)
Khi đó \(\left( * \right){\text{ }} \Leftrightarrow {\text{ }}{d_1},{\text{ }}{d_2}\) cắt \(\left( C \right)\) tại bốn điểm phân biệt \( \Leftrightarrow – m > – 16 \Leftrightarrow m < 16.\)Vậy có \(15\) giá trị \(m\) nguyên dương thỏa mãn điều kiện.
