Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-luyen-thi-tot-nghiep-thpt-2023-mon-toan-online-de-8
Đề Kiểm Tra: Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8
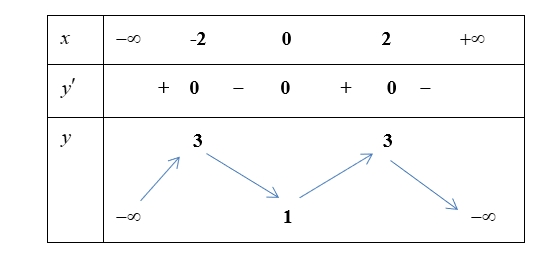 Số điểm cực tiểu của hàm số đã cho là:
Số điểm cực tiểu của hàm số đã cho là:\(3\)
\(\left( { - 1;2; - 3} \right).\)
\(\frac{{32\pi }}{3}\).
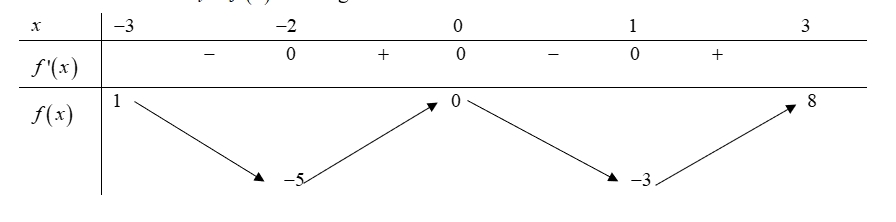 Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { – 3\,;3} \right]\) bằng
Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { – 3\,;3} \right]\) bằng\(3\)
\(\frac{1}{3}\).
\(1\).
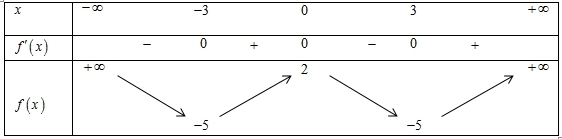 Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số đã cho đồng biến trên khoảng nào dưới đây?\(( - 3;0)\).
\(y = - 3\).
\(C_{13}^2\).
\(\overrightarrow j = \left( {0;1;0} \right)\).
\(x = 4\).
\(40\pi {a^2}\).
\(\int\limits_a^b {k.f\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx} ,k \in \mathbb{R}\).
\(\left( { - \infty ;1} \right)\).
\(R = 3\).
\(1\).
\(y = {x^3} - 3{x^2} - 1\).
\(20{x^3} - 12x + C\).
\({S_{xq}} = 2\pi Rh\).
\(4{a^3}\).
\(P = 9\).
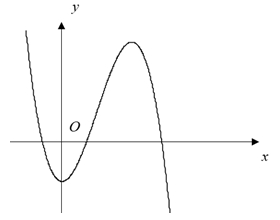
Số điểm cực đại của hàm số đã cho là
\(1\).
\( - \cos x - x\sin x + C\).
\(x - 2 = 0\).
\(1\).
\(2x - y - z + 5 = 0\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 3\).
\(\frac{3}{{11}}\).
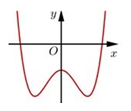
Xác định dấu của \(a\,,\,b\,,\,c\).
\(a > 0,b < 0,c < 0\).
4
\({\text{16}}\)
\({u_3} = 5\)
\(3\)
\(\sqrt 3 {a^2}.\)
\(T = \frac{5}{6}.\)
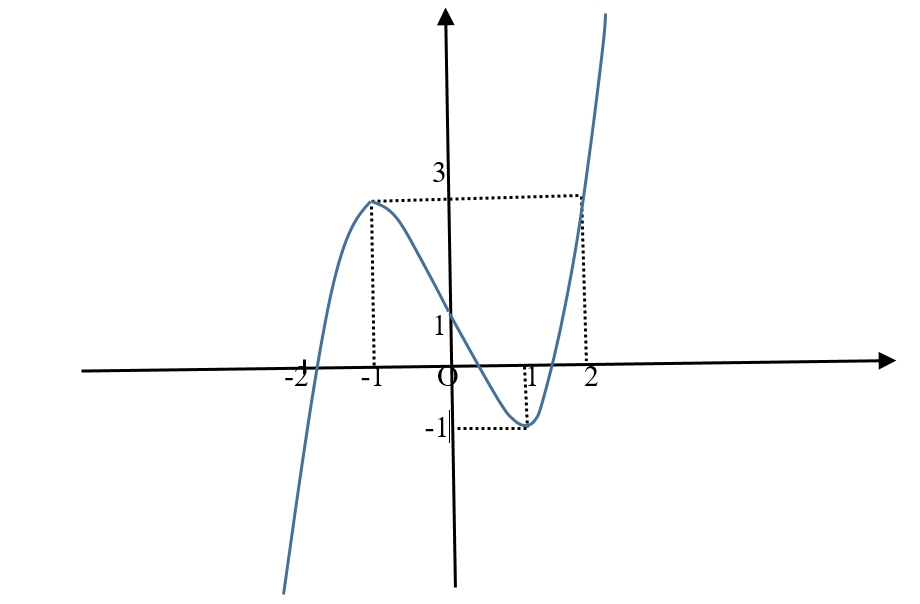
\(2022.\)
\(a \in \left( {16;\left. {18} \right]} \right.\).
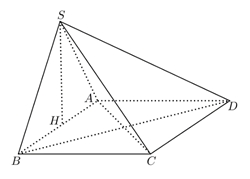
Tính khoảng cách từ \(A\) đến \(\left( {SBC} \right)\)
\(\frac{{\sqrt 3 a}}{4}\).
\(x - y - z = 0.\)
\(\frac{9}{2}\).
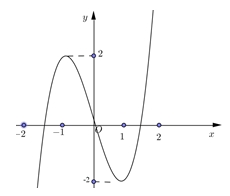
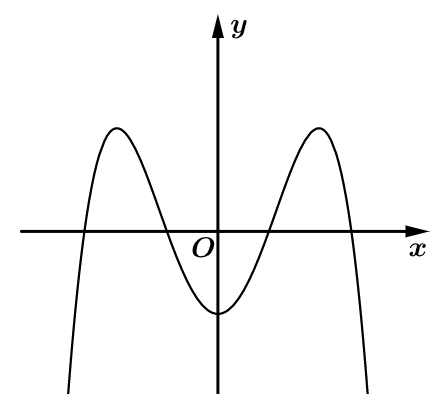
Phương trình \(f\left( {f\left( x \right)} \right) = 0\) có bao nhiêu nghiệm thực?
\(9\)
Vậy phương trình đã cho có \(9\) nghiệm phân biệt.
\(\frac{7}{4}\)
\(m = \pm 3\)
\({60^o}\)
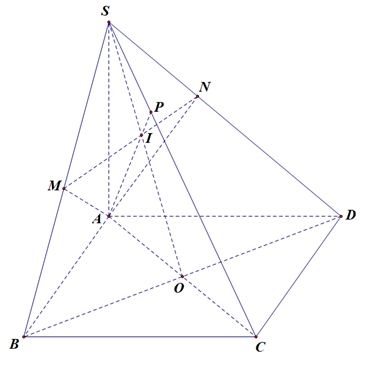
Cách 1:Gọi \(AC \cap BD = O,\,\,SO \cap MN = I,\,\,AI \cap SC = P\).\(AN \bot \left( {SCD} \right) \Rightarrow AN \bot SC\) và \(AM \bot \left( {SBC} \right) \Rightarrow AM \bot SC\), do đó: \(SC \bot \left( {AMN} \right)\) hay \(SC \bot \left( {AMPN} \right)\).Suy ra: \(\left( {SB,\left( {AMN} \right)} \right) = \left( {SM,\left( {AMPN} \right)} \right) = \widehat {SMP}\).Ta có: \(SM = \frac{{S{A^2}}}{{SB}} = \frac{{2{a^2}}}{{\sqrt {2{a^2} + {a^2}} }} = \frac{{2a\sqrt 3 }}{3}\); \(SP = \frac{{S{A^2}}}{{SC}} = \frac{{2{a^2}}}{{\sqrt {2{a^2} + 2{a^2}} }} = a\).Nên \(\sin \widehat {SMP} = \frac{{SP}}{{SM}} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {SMP} = {60^o}\).
Cách 2:Ta có \(AM = AN = \frac{{a\sqrt 6 }}{3}\) và \(\frac{{SM}}{{SB}} = \frac{{SN}}{{SD}} = \frac{{S{A^2}}}{{S{B^2}}} = \frac{2}{3} \Rightarrow MN\parallel BD;\frac{{MN}}{{BD}} = \frac{2}{3}\)Suy ra \(MN = \frac{2}{3}BD = \frac{{2a\sqrt 2 }}{3}\)
Diện tích tam giác \(AMN:{S_{\Delta AMN}} = \frac{{2{a^2}\sqrt 2 }}{9}\)\({V_{S.AMN}} = \frac{2}{3}.\frac{2}{3}.{V_{S.ABD}} \Rightarrow {V_{S.AMN}} = \frac{1}{3}.\frac{4}{9}.\frac{1}{2}.a\sqrt 2 .{a^2} = \frac{{2\sqrt 2 .{a^3}}}{{27}}\)
\(\Rightarrow d\left( {S;\left( {AMN} \right)} \right) = \frac{{3{V_{S.AMN}}}}{{{S_{\Delta AMN}}}} = a\)
Do đó,
\(\sin \left( {\widehat {SB;(AMN)}} \right) = \frac{{d\left( {S;(AMN)} \right)}}{{SM}} = \frac{{\sqrt 3 }}{2}\)
\( \Rightarrow \left( {\widehat {SB;(AMN)}} \right) = {60^0}\)
\(4{a^3}\)
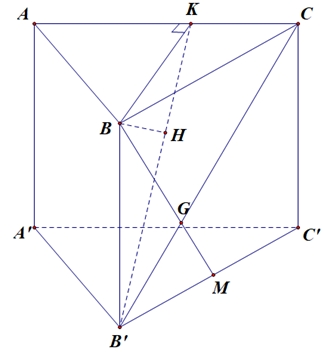
Kẻ \(BK \bot AC\), mà \(AC \bot BB'\) nên \(AC \bot \left( {BB'K} \right) \Rightarrow \left( {B'AC} \right) \bot \left( {BB'K} \right)\).
\(\left( {B'AC} \right) \cap \left( {BB'K} \right) = B'K\), trong mp\(\left( {B'BK} \right)\) kẻ \(BH \bot B'K\), khi đó: \(BH \bot \left( {B'AC} \right)\).
Do đó: \(d\left( {B;\left( {B'AC} \right)} \right) = BH = \frac{{3a\sqrt {15} }}{5}\).
\(\Delta AKB\) vuông tại \(K\) nên \(BK = A
B:)\sin {60^o} = 3a.\frac{{\sqrt 3 }}{2} = \frac{{3a\sqrt 3 }}{2}\).
Mặt khác: \(\frac{1}{{B{H^2}}} = \frac{1}{{B{K^2}}} + \frac{1}{{B{{B'}^2}}} \Leftrightarrow \frac{1}{{{{\left( {\frac{{3a\sqrt {15} }}{5}} \right)}^2}}} = \frac{1}{{{{\left( {\frac{{3a\sqrt 3 }}{2}} \right)}^2}}} + \frac{1}{{B{{B'}^2}}} \Leftrightarrow BB' = 3a\sqrt 3 \).
Vậy \(V = BB'.{S_{\Delta ABC}} = 3a\sqrt 3 .\frac{1}{2}.3a.4a.\sin {60^o} = 27{a^3}\).
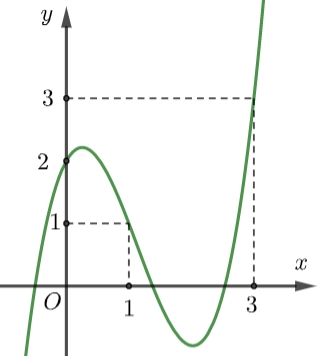
\(\left( {\frac{1}{2};2} \right)\)
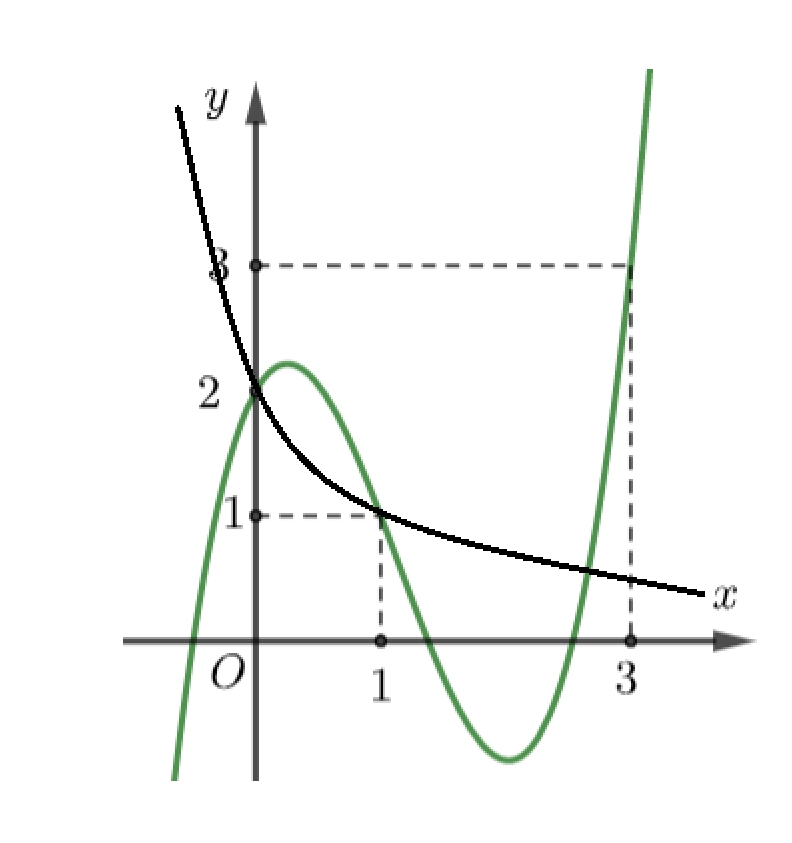 Dựa vào đồ thị ta có GTLN của \(g\left( x \right)\) là tại \(g\left( 1 \right)\) hoặc \(g\left( 3 \right)\).Ta thấy: \(\int\limits_1^a {\left[ {\frac{2}{{t + 1}} – f'\left( t \right)} \right]dt} > \int\limits_a^3 {\left[ {f'\left( t \right) – \frac{2}{{t + 1}}} \right]dt} \)\( \Leftrightarrow \left. {\left( {2\ln \left| {t + 1} \right| – f\left( t \right)} \right)} \right|_1^a > \left. {\left( {f\left( t \right) – 2\ln \left| {t + 1} \right|} \right)} \right|_a^3\)\( \Leftrightarrow 2\ln \left( {a + 1} \right) – f\left( a \right) – 2\ln 2 + f\left( 1 \right) > f\left( 3 \right) – 4\ln 2 – f\left( a \right) + 2\ln \left( {a + 1} \right)\)\( \Leftrightarrow f\left( 1 \right) – f\left( 3 \right) + 2\ln 2 > 0\) (*)Xét \(g\left( x \right) = f\left( {\frac{x}{2} + 1} \right) – \ln \left( {{x^2} + 8x + 16} \right)\), khi đó:+) \(g\left( 1 \right) = f\left( 1 \right) – 4\ln 2\).+) \(g\left( 3 \right) = f\left( 3 \right) – 8\ln 2\).\( \Rightarrow g\left( 1 \right) – g\left( 3 \right) = f\left( 1 \right) – f\left( 3 \right) + 4\ln 2\), từ (*) ta suy ra \( \Rightarrow g\left( 1 \right) – g\left( 3 \right) > 0 \Leftrightarrow g\left( 1 \right) > g\left( 3 \right)\).Vậy hàm số đã cho đạt GTLN tại \(t = 1 \Rightarrow x = 0\).
Dựa vào đồ thị ta có GTLN của \(g\left( x \right)\) là tại \(g\left( 1 \right)\) hoặc \(g\left( 3 \right)\).Ta thấy: \(\int\limits_1^a {\left[ {\frac{2}{{t + 1}} – f'\left( t \right)} \right]dt} > \int\limits_a^3 {\left[ {f'\left( t \right) – \frac{2}{{t + 1}}} \right]dt} \)\( \Leftrightarrow \left. {\left( {2\ln \left| {t + 1} \right| – f\left( t \right)} \right)} \right|_1^a > \left. {\left( {f\left( t \right) – 2\ln \left| {t + 1} \right|} \right)} \right|_a^3\)\( \Leftrightarrow 2\ln \left( {a + 1} \right) – f\left( a \right) – 2\ln 2 + f\left( 1 \right) > f\left( 3 \right) – 4\ln 2 – f\left( a \right) + 2\ln \left( {a + 1} \right)\)\( \Leftrightarrow f\left( 1 \right) – f\left( 3 \right) + 2\ln 2 > 0\) (*)Xét \(g\left( x \right) = f\left( {\frac{x}{2} + 1} \right) – \ln \left( {{x^2} + 8x + 16} \right)\), khi đó:+) \(g\left( 1 \right) = f\left( 1 \right) – 4\ln 2\).+) \(g\left( 3 \right) = f\left( 3 \right) – 8\ln 2\).\( \Rightarrow g\left( 1 \right) – g\left( 3 \right) = f\left( 1 \right) – f\left( 3 \right) + 4\ln 2\), từ (*) ta suy ra \( \Rightarrow g\left( 1 \right) – g\left( 3 \right) > 0 \Leftrightarrow g\left( 1 \right) > g\left( 3 \right)\).Vậy hàm số đã cho đạt GTLN tại \(t = 1 \Rightarrow x = 0\).\(61\).
\(6.\)
\(I = - \frac{{16}}{5}\).
Đặt:
\(\left\{ \begin{gathered}
u = {x^3} – 3{x^2} \hfill \\
{d}v = \frac{{f’\left( x \right)}}{{f\left( x \right)}}{d}x \hfill \\
\end{gathered} \right.\)\( \Rightarrow \left\{ \begin{gathered}
{d}u = \left( {3{x^2} – 6x} \right){d}x \hfill \\
v = \ln \left| {f\left( x \right)} \right| \hfill \\
\end{gathered} \right.\)\( \Rightarrow \left\{ \begin{gathered}
{d}u = \left( {3{x^2} – 6x} \right){d}x \hfill \\
v = \ln f\left( x \right) \hfill \\
\end{gathered} \right.\)
Suy ra: \(I = \left. {\left( {{x^3} – 3{x^2}} \right)\ln f\left( x \right)} \right|_0^2 – \int\limits_0^2 {\left( {3{x^2} – 6x} \right)\ln f\left( x \right){d}x} \)\( = – \int\limits_0^2 {\left( {3{x^2} – 6x} \right)\ln f\left( x \right){d}x} \) \(\left( 1 \right)\)
Đặt \(x = 2 – t\)\( \Rightarrow {d}x = – {d}t\).
Khi \(x = 0 \to t = 2\) và \(x = 2 \to t = 0\).
Khi đó, \(J = – \int\limits_2^0 {\left( {3{t^2} – 6t} \right)\ln f\left( {2 – t} \right)( – {d}t)} \)\( = – \int\limits_0^2 {\left( {3{t^2} – 6t} \right)\ln f\left( {2 – t} \right){d}t} \).
Vì tích phân không phụ thuộc vào biến nên \(I = – \int\limits_0^2 {\left( {3{x^2} – 6x} \right)\ln f\left( {2 – x} \right){d}x} \) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), ta cộng vế theo vế, ta được: \(2I = – \int\limits_0^2 {\left( {3{x^2} – 6x} \right)\left[ {\ln f\left( x \right) + \ln f\left( {2 – x} \right)} \right]{d}x} \).
Hay \(I = – \frac{1}{2}\int\limits_0^2 {\left( {3{x^2} – 6x} \right)\left( {2{x^2} – 4x} \right){d}x} = – \frac{{16}}{5}\)
\(2023\).
\(\ln \left( {x + m} \right) = {e^x} – m = t \Leftrightarrow \left\{ \begin{gathered} x + m = {e^t} \hfill \\ t + m = {e^x} \hfill \\ \end{gathered} \right. \Leftrightarrow {e^t} + t = {e^x} + x\)
Xét hàm số: \(f(t) = {e^t} + t \Rightarrow {f^/}(t) = e{}^t + 1 > 0\,\,(\forall t \in \mathbb{R})\)
Nên ta có: \(f(t) = f(x) \Leftrightarrow t = x\)
Phương trình \({e^x} – m = x \Leftrightarrow {e^x} – x = m\) có nghiệm khi và chỉ khi \(m \geqslant 1\)
Vậy có: 2023 giá trị \(m\).
