Đề Trắc Nghiệm Online Cực Trị Của Hàm Số-Đề 4
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-trac-nghiem-online-cuc-tri-cua-ham-so-de-4
Đề Kiểm Tra: Đề Trắc Nghiệm Online Cực Trị Của Hàm Số-Đề 4
Câu 1:
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau: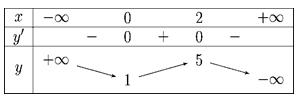 Giá trị cực đại của hàm số bằng
Giá trị cực đại của hàm số bằng
 Giá trị cực đại của hàm số bằng
Giá trị cực đại của hàm số bằng5.
Câu 2:
Cho hàm số \(y = f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. 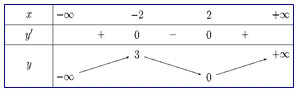 Tìm giá trị cực đại \({y_{CĐ}}\)và giá trị cực tiểu \({y_{CT}}\) của hàm số đã cho
Tìm giá trị cực đại \({y_{CĐ}}\)và giá trị cực tiểu \({y_{CT}}\) của hàm số đã cho
 Tìm giá trị cực đại \({y_{CĐ}}\)và giá trị cực tiểu \({y_{CT}}\) của hàm số đã cho
Tìm giá trị cực đại \({y_{CĐ}}\)và giá trị cực tiểu \({y_{CT}}\) của hàm số đã cho\({y_{CĐ}} = 3\) và \({y_{CT}} = 0\)
Câu 3:
Các điểm cực tiểu của hàm số \(y = {x^4} + 3{x^2} + 2\) là
\(x = 0\).
Tập xác định: \(D = \mathbb{R}\).
\(y' = 4{x^3} + 6x = x\left( {4{x^2} + 6} \right)\).
\(y' = 0 \Leftrightarrow x\left( {4{x^2} + 6} \right) = 0 \Leftrightarrow x = 0\). Vậy hàm số có điểm cực tiểu là \(x = 0\).
Vậy hàm số có điểm cực tiểu là \(x = 0\).
\(y' = 4{x^3} + 6x = x\left( {4{x^2} + 6} \right)\).
\(y' = 0 \Leftrightarrow x\left( {4{x^2} + 6} \right) = 0 \Leftrightarrow x = 0\).
 Vậy hàm số có điểm cực tiểu là \(x = 0\).
Vậy hàm số có điểm cực tiểu là \(x = 0\).Câu 4:
Cho hàm số \(y = – {x^4} + 2{x^2} + 3\). Mệnh đề nào dưới đây là mệnh đề đúng?
Hàm số không có cực đại, chỉ có 1 cực tiểu.
Có \(y' = – 4{x^3} + 4x\), \(y' = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ x = 1 \hfill \\ x = – 1 \hfill \\ \end{gathered} \right.\)Vì hàm số là hàm trùng phương có hệ số \(a < 0\) và phương trình \(y' = 0\) có 3 nghiệm phân biệt nên hàm số có 2 cực đại và 1 cực tiểu.
Câu 5:
Giá trị cực tiểu của hàm số \(y = {x^3} – 3{x^2} – 9x + 2\) là
\(3\).
TXĐ: \(D = \mathbb{R}\).\(y’ = 3{x^2} – 6x – 9\). Cho \(y’ = 0 \Leftrightarrow \left[ \begin{gathered} x = – 1 \hfill \\ x = 3 \hfill \\ \end{gathered} \right.\)
Câu 6:
Điểm cực đại của đồ thị hàm số \(y = {x^3} – 3x + 2\) là:
\(x = - 1\).
Ta có \(y’ = 3{x^2} – 3\)
Câu 7:
Cho hàm số \(y = {x^4} – 2m{x^2} + m\). Tìm tất cả các giá trị thực của \(m\) để hàm số có \(3\) cực trị
\(m \leqslant 0\).
Tập xác định \(D = \mathbb{R}\).
Câu 8:
Hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = \left( {x – 1} \right)\left( {x – 2} \right)\left( {x – 3} \right)\), \(\forall x \in \mathbb{R}\). Hàm số \(y = f\left( x \right)\) có tất cả bao nhiêu điểm cực tiểu?
\(1\).
Ta có: \(f’\left( x \right) = \left( {x – 1} \right)\left( {x – 2} \right)\left( {x – 3} \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = 2 \hfill \\ x = 3 \hfill \\ \end{gathered} \right.\)
Câu 9:
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm \(f'(x)\) như sau: Hàm số đã cho có bao nhiêu cực trị?
Hàm số đã cho có bao nhiêu cực trị?
 Hàm số đã cho có bao nhiêu cực trị?
Hàm số đã cho có bao nhiêu cực trị?3.
Câu 10:
Cho hàm số \(f(x)\)xác định và liên tục trên \(\mathbb{R}\),có đồ thị của hàm số\(f'(x)\)như hình vẽ. 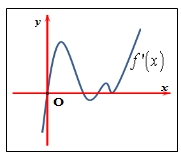 Hàm số \(f(x)\) có bao nhiêu cực trị ?
Hàm số \(f(x)\) có bao nhiêu cực trị ?
 Hàm số \(f(x)\) có bao nhiêu cực trị ?
Hàm số \(f(x)\) có bao nhiêu cực trị ?2.
Giải thích & Đáp án chi tiết
Câu 1
Đáp án đúng: ʍ
5.
Câu 2
Đáp án đúng: ʋ
\({y_{CĐ}} = 3\) và \({y_{CT}} = 0\)
Câu 3
Đáp án đúng: ʊ
\(x = 0\).
Câu 4
Đáp án đúng: ʋ
Hàm số không có cực đại, chỉ có 1 cực tiểu.
Câu 5
Đáp án đúng: ʌ
\(3\).
Câu 6
Đáp án đúng: ʊ
\(x = - 1\).
Câu 7
Đáp án đúng: ʊ
\(m \leqslant 0\).
Câu 8
Đáp án đúng: ʍ
\(1\).
Câu 9
Đáp án đúng: ʍ
3.
Câu 10
Đáp án đúng: ʋ
2.
