Kiểm Tra Trắc Nghiệm Tính Đơn Điệu Của Hàm Số Online-Đề 4
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/kiem-tra-trac-nghiem-tinh-don-dieu-cua-ham-so-online-de-4
Đề Kiểm Tra: Kiểm Tra Trắc Nghiệm Tính Đơn Điệu Của Hàm Số Online-Đề 4
Câu 1:
Cho hàm số\(y = f(x)\)có bảng biến thiên như hình sau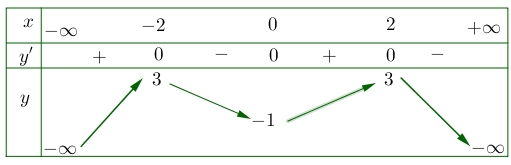 Hàm số\(y = f(x)\)đồng biến trên khoảng nào dưới đây?
Hàm số\(y = f(x)\)đồng biến trên khoảng nào dưới đây?
 Hàm số\(y = f(x)\)đồng biến trên khoảng nào dưới đây?
Hàm số\(y = f(x)\)đồng biến trên khoảng nào dưới đây?\(\left( { - \infty ;0} \right)\).
Dựa vào bảng biến thiên của hàm số ta có hàm số đồng biến trên các khoảng \(\left( { – \infty ; – 2} \right)\)và\(\left( {0;2} \right)\).
Câu 2:
Cho hàm số \(y = f\left( x \right)\) xác định \(\mathbb{R}\backslash \left\{ 0 \right\}\), liên tục trên từng khoảng xác định và có bảng biến thiên như hình vẽ:
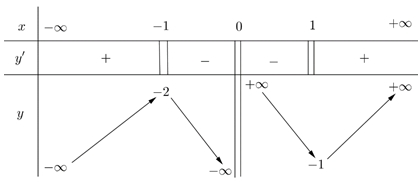
Khẳng định nào sau đây là đúng?

Khẳng định nào sau đây là đúng?
Hàm số nghịch biến trên \(\left( {0;1} \right)\).
Dựa vào bảng biến thiên, ta thấy hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\).
Câu 3:
Cho hàm số \(y = f(x)\) có bảng biến thiên như hình vẽ.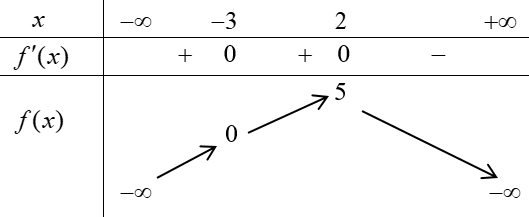 Xét các mệnh đề:
Xét các mệnh đề:
1. Hàm số đồng biến trên khoảng \(( – 3; – 2)\).
2. Hàm số đồng biến trên khoảng \(( – \infty ;5).\)
3. Hàm số nghịch biến trên khoảng \((5; + \infty ).\)
4. Hàm số đồng biến trên khoảng \(( – \infty ; – 2).\)
Có bao nhiêu mệnh đề sai trong các mệnh đề trên?
 Xét các mệnh đề:
Xét các mệnh đề:1. Hàm số đồng biến trên khoảng \(( – 3; – 2)\).
2. Hàm số đồng biến trên khoảng \(( – \infty ;5).\)
3. Hàm số nghịch biến trên khoảng \((5; + \infty ).\)
4. Hàm số đồng biến trên khoảng \(( – \infty ; – 2).\)
Có bao nhiêu mệnh đề sai trong các mệnh đề trên?
2.
Dựa vào bảng biến thiên ta thấy+) Hàm số đồng biến trên khoảng \(( – 3;2)\) nên đồng biến trên \(( – 3; – 2)\)do đó mệnh đề 1 đúng.+) Hàm số đồng biến trên \(( – \infty ;5)\) là đáp án sai vì trên khoảng đó có khoảng \((2;5)\)hàm số nghịch biến.+) Hàm số nghịch biến trên khoảng \((5; + \infty )\) là đáp án đúng vì hàm số nghịch biến trên \((2; + \infty )\)nên cũng nghịch biến trên \((5; + \infty )\)+) Hàm số đồng biến trên khoảng \(( – \infty ; – 2)\)là đáp án đúng.Vậy số mệnh đề sai là 1.
Câu 4:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau: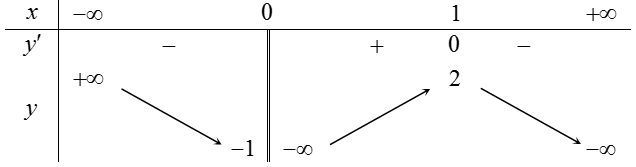 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?Hàm số đồng biến trên \(\left( {0;1} \right)\).
Câu 5:
Cho đồ thị hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?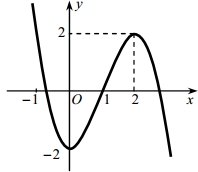

\(\left( {2;\,\, + \infty } \right)\).
Nhìn vào đồ thị ta thấy hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0;\,\,2} \right)\).
Câu 6:
Cho hàm số \(y = \frac{{x – 1}}{{2x + 1}}\). Mệnh đề sau đây đúng?
Hàm số đồng biến trên \(\left( { - \infty ;\frac{1}{2}} \right)\).
Ta có: \(y' = \frac{3}{{{{(2x + 1)}^2}}} > 0\) với mọi \(x \ne – \frac{1}{2}\).
Câu 7:
Cho hàm số \(y = {x^2}\left( {3 – x} \right)\). Mệnh đề nào sau đây là đúng?
Hàm số đã cho đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
Ta có \(y' = – 3{x^2} + 6x\) ; \(y' = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ x = 2 \hfill \\ \end{gathered} \right.\).Bảng biến thiên: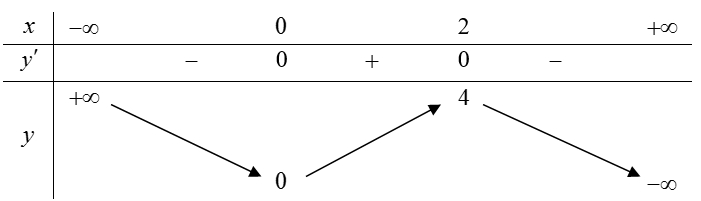 .Vậy hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right)\).
.Vậy hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right)\).
 .Vậy hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right)\).
.Vậy hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right)\).Câu 8:
Hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) trên\(\mathbb{R}\). Hình vẽ bên dưới là đồ thị của hàm số \(f'\left( x \right)\) trên \(\mathbb{R}\). Chọn đáp án đúng.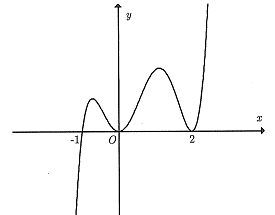

Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Dựa vào đồ thị hàm số \(f'(x)\) ta có bảng biến thiên sau: 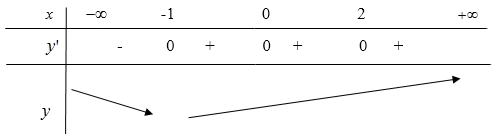 Suy ra hàm số đồng biến trên khoảng \(\left( { – 1; + \infty } \right)\).
Suy ra hàm số đồng biến trên khoảng \(\left( { – 1; + \infty } \right)\).
 Suy ra hàm số đồng biến trên khoảng \(\left( { – 1; + \infty } \right)\).
Suy ra hàm số đồng biến trên khoảng \(\left( { – 1; + \infty } \right)\).Câu 9:
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau
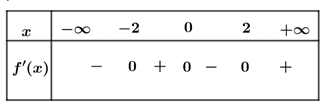
Hàm số \(g\left( x \right) = f\left( {3x – 2} \right)\) đồng biến trên khoảng nào dưới đây

Hàm số \(g\left( x \right) = f\left( {3x – 2} \right)\) đồng biến trên khoảng nào dưới đây
\(\left( {0;\,\,1} \right)\).
+ Xét hàm số \(y = g\left( x \right) = f\left( {3x – 2} \right)\).+ \(g'\left( x \right) = 3f'\left( {3x – 2} \right)\); \(g'\left( x \right) = 0 \Leftrightarrow f'\left( {3x – 2} \right) = 0 \Leftrightarrow \left[ \begin{gathered} 3x – 2 = – 2 \hfill \\ 3x – 2 = 0 \hfill \\ 3x – 2 = 2 \hfill \\ \end{gathered} \right.\)\( \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ x = \frac{2}{3} \hfill \\ x = \frac{4}{3} \hfill \\ \end{gathered} \right.\) .
+ Bảng xét dấu \(g'\left( x \right)\):
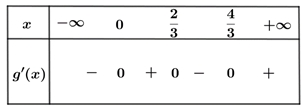
Từ bảng xét dấu của \(g'\left( x \right)\) ta thấy hàm số \(y = g\left( x \right)\) đồng biến trên các khoảng \(\left( {0;\,\,\frac{2}{3}} \right)\) và \(\left( {\frac{4}{3};\,\, + \infty } \right)\).
+ Bảng xét dấu \(g'\left( x \right)\):

Từ bảng xét dấu của \(g'\left( x \right)\) ta thấy hàm số \(y = g\left( x \right)\) đồng biến trên các khoảng \(\left( {0;\,\,\frac{2}{3}} \right)\) và \(\left( {\frac{4}{3};\,\, + \infty } \right)\).
Câu 10:
Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) để hàm số \(y = \sqrt {{x^2} + 2x + {m^2} – 8} \) đồng biến trên \(\mathbb{R}\). Số phần tử của \(S\) là:
vô số.
Hàm số \(y = \sqrt {{x^2} + 2x + {m^2} – 8} \) đồng biến trên \(\mathbb{R}\)
\( \Leftrightarrow \)\({x^2} + 2x + {m^2} – 8 \geqslant 0\forall x \in \mathbb{R}\)
\( \Leftrightarrow \Delta ‘ \leqslant 0\) (Do \(a = 1 > 0\))
\( \Leftrightarrow – {m^2} + 9 \geqslant 0 \Leftrightarrow – 3 \leqslant m \leqslant 3\)
Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ { – 3; – 2; – 1;0;1;2;3} \right\}\)
Vậy tập \(S = \left\{ { – 3; – 2; – 1;0;1;2;3} \right\}\) có 7 phần tử.
\( \Leftrightarrow \)\({x^2} + 2x + {m^2} – 8 \geqslant 0\forall x \in \mathbb{R}\)
\( \Leftrightarrow \Delta ‘ \leqslant 0\) (Do \(a = 1 > 0\))
\( \Leftrightarrow – {m^2} + 9 \geqslant 0 \Leftrightarrow – 3 \leqslant m \leqslant 3\)
Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ { – 3; – 2; – 1;0;1;2;3} \right\}\)
Vậy tập \(S = \left\{ { – 3; – 2; – 1;0;1;2;3} \right\}\) có 7 phần tử.
Giải thích & Đáp án chi tiết
Câu 1
Đáp án đúng: ʊ
\(\left( { - \infty ;0} \right)\).
Câu 2
Đáp án đúng: ʊ
Hàm số nghịch biến trên \(\left( {0;1} \right)\).
Câu 3
Đáp án đúng: ʊ
2.
Câu 4
Đáp án đúng: ʊ
Hàm số đồng biến trên \(\left( {0;1} \right)\).
Câu 5
Đáp án đúng: ʊ
\(\left( {2;\,\, + \infty } \right)\).
Câu 6
Đáp án đúng: ʊ
Hàm số đồng biến trên \(\left( { - \infty ;\frac{1}{2}} \right)\).
Câu 7
Đáp án đúng: ʊ
Hàm số đã cho đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
Câu 8
Đáp án đúng: ʌ
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Câu 9
Đáp án đúng: ʊ
\(\left( {0;\,\,1} \right)\).
Câu 10
Đáp án đúng: ʊ
vô số.
