Kiểm Tra 15 Phút Cực Trị Của Hàm Số Online-Đề 1
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/kiem-tra-15-phut-cuc-tri-cua-ham-so-online-de-1
Đề Kiểm Tra: Kiểm Tra 15 Phút Cực Trị Của Hàm Số Online-Đề 1
Câu 1:
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau: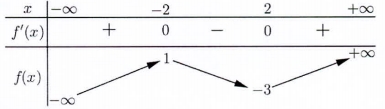 Điểm cực đại của hàm số đã cho là:
Điểm cực đại của hàm số đã cho là:
 Điểm cực đại của hàm số đã cho là:
Điểm cực đại của hàm số đã cho là:\(x = 2\).
Nhận thấy \(f'\left( x \right)\) đổi dấu từ dấu dương sang dấu âm khi đi qua \(x = – 2\) suy ra \(x = – 2\) là điểm cực đại của hàm số.
Câu 2:
Hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?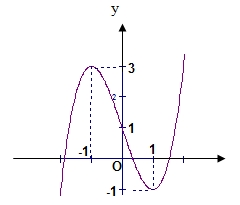

Đồ thị hàm số có điểm cực tiểu là \(\left( { - 1;3} \right)\).
Dựa vào đồ thị ta có: Đồ thị hàm số có điểm cực tiểu là \(\left( {1; – 1} \right)\) và điểm cực đại là \(\left( { – 1;3} \right)\).
Câu 3:
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như sau.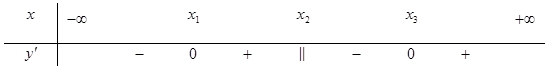 Khi đó số điểm cực trị của hàm số \(y = f\left( x \right)\) là
Khi đó số điểm cực trị của hàm số \(y = f\left( x \right)\) là
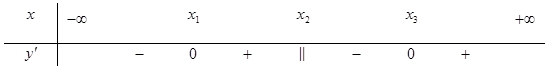 Khi đó số điểm cực trị của hàm số \(y = f\left( x \right)\) là
Khi đó số điểm cực trị của hàm số \(y = f\left( x \right)\) là\(1\).
Do hàm số xác định trên \(\mathbb{R}\) và có biểu thức đạo hàm đổi dấu ba lần tại \({x_1}\); \({x_2}\); \({x_3}\) nên hàm số \(y = f\left( x \right)\) có ba điểm cực trị.
Câu 4:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên.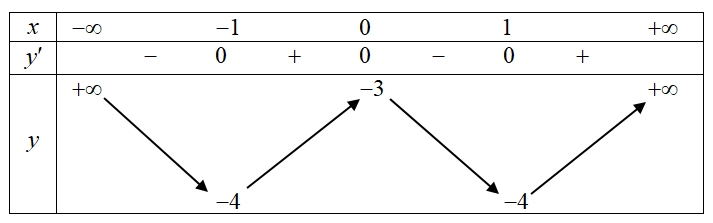 Tọa độ điểm cực đại của đồ thị hàm số \(y = f\left( x \right)\) là
Tọa độ điểm cực đại của đồ thị hàm số \(y = f\left( x \right)\) là
 Tọa độ điểm cực đại của đồ thị hàm số \(y = f\left( x \right)\) là
Tọa độ điểm cực đại của đồ thị hàm số \(y = f\left( x \right)\) là\(\left( { - 1\,;\, - 4} \right)\)
Câu 5:
Cho hàm số \(y = f(x)\) có đồ thị như hình bên. Hàm số có bao nhiêu điểm cực tiểu trên khoảng \(\left( {a;b} \right)\)?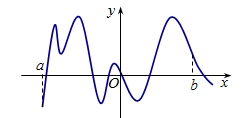

4.
Câu 6:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm là \(f'\left( x \right) = x{\left( {x + 1} \right)^2}\left( {x – 1} \right)\). Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
3.
Câu 7:
Gọi \({x_1}\) là điểm cực đại, \({x_2}\) là điểm cực tiểu của hàm số \(y = {x^3} – 3x + 2\). Tính \({x_1} + 2{x_2}\).
\(0\).
\(y' = 3{x^2} – 3\).\(y' = 0\)\( \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = – 1 \hfill \\ \end{gathered} \right.\).Bảng xét dấu  Dựa vào bảng xét dấu, điểm cực đại là \({x_1} = – 1\) và điểm cực đại là \({x_2} = 1\) nên \({x_1} + 2{x_2} = 1\).
Dựa vào bảng xét dấu, điểm cực đại là \({x_1} = – 1\) và điểm cực đại là \({x_2} = 1\) nên \({x_1} + 2{x_2} = 1\).
 Dựa vào bảng xét dấu, điểm cực đại là \({x_1} = – 1\) và điểm cực đại là \({x_2} = 1\) nên \({x_1} + 2{x_2} = 1\).
Dựa vào bảng xét dấu, điểm cực đại là \({x_1} = – 1\) và điểm cực đại là \({x_2} = 1\) nên \({x_1} + 2{x_2} = 1\).Câu 8:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ. Hàm số có bao nhiêu điểm cực trị?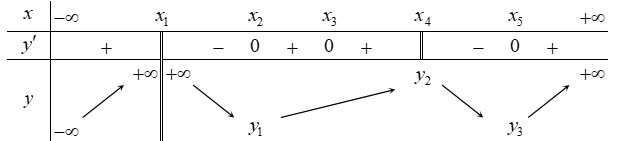
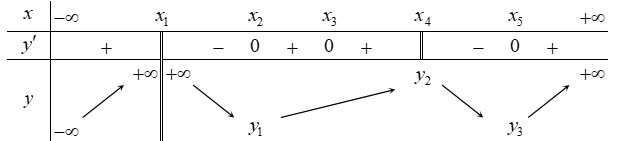
\(2\).
Tập xác định \(D = \mathbb{R}\backslash \left\{ {{x_1}} \right\}\).Theo định lí về điều kiện đủ để hàm số có cực trị và dựa vào bảng biến thiên ta có các điểm cực trị của hàm số là: \({x_2}\); \({x_4}\); \({x_5}\).
Câu 9:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), đồ thị của đạo hàm \(f'\left( x \right)\) như hình vẽ sau: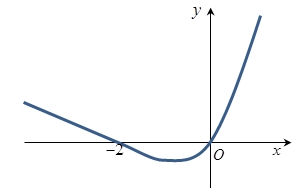 Trong các mệnh đề sau, mệnh đề nào sai?
Trong các mệnh đề sau, mệnh đề nào sai?
 Trong các mệnh đề sau, mệnh đề nào sai?
Trong các mệnh đề sau, mệnh đề nào sai?\(f\) đạt cực tiểu tại \(x = - 2\).
Từ đồ thị ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = – 2 \hfill \\ x = 0 \hfill \\ \end{gathered} \right.\) và \(f'\left( x \right) > 0 \Leftrightarrow \left[ \begin{gathered} x < - 2 \hfill \\ x > 0 \hfill \\ \end{gathered} \right.\), \(f'\left( x \right) < 0 \Leftrightarrow - 2 < x < 0\).Từ đó suy ra bảng biến thiên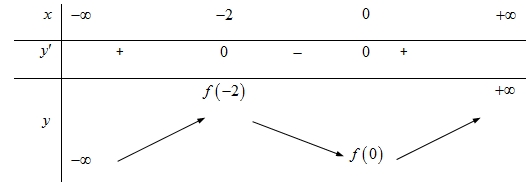 Vậy hàm số đạt cực đại tại \(x = – 2\).
Vậy hàm số đạt cực đại tại \(x = – 2\).
 Vậy hàm số đạt cực đại tại \(x = – 2\).
Vậy hàm số đạt cực đại tại \(x = – 2\).Câu 10:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\)có đạo hàm \(f'\left( x \right)\) liên tục trên \(\mathbb{R}\)và có bảng xét dấu như hình vẽ bên Hỏi hàm số \(y = f\left( {{x^2} – 2\left| x \right|} \right)\)có tất cả bao nhiêu điểm cực trị
Hỏi hàm số \(y = f\left( {{x^2} – 2\left| x \right|} \right)\)có tất cả bao nhiêu điểm cực trị
 Hỏi hàm số \(y = f\left( {{x^2} – 2\left| x \right|} \right)\)có tất cả bao nhiêu điểm cực trị
Hỏi hàm số \(y = f\left( {{x^2} – 2\left| x \right|} \right)\)có tất cả bao nhiêu điểm cực trị\(7\).
Tập xác định của hàm số: \(D = \mathbb{R}\).* \(y = h\left( x \right) = f\left( {{{\left| x \right|}^2} – 2\left| x \right|} \right)\)\(y' = h'\left( x \right) = f'\left( {{{\left| x \right|}^2} – 2\left| x \right|} \right).\frac{x}{{\left| x \right|}}.\left( {2\left| x \right| – 2} \right).\)\(h'\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = – 1 \hfill \\ {\left| x \right|^2} – 2\left| x \right| = 0 \hfill \\ {\left| x \right|^2} – 2\left| x \right| = 1 \hfill \\ {\left| x \right|^2} – 2\left| x \right| = 2 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = – 1 \hfill \\ x = 2 \hfill \\ x = – 2 \hfill \\ x = 1 + \sqrt 2 \hfill \\ x = – 1 – \sqrt 2 \hfill \\ x = 1 + \sqrt 3 \hfill \\ x = – 1 – \sqrt 3 \hfill \\ \end{gathered} \right.\).Ta thấy phương trình \(h'\left( x \right) = 0\) có 8 nghiệm đơn \(\left( 1 \right)\).\(h'\left( x \right)\) không tồn tại tại \(x = 0\) mà \(x = 0\)thuộc tập xác định đồng thời qua đó \(h'\left( x \right)\) đổi dấu \(\left( 2 \right)\).Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra hàm số đã cho có \(9\) điểm cực trị.
Giải thích & Đáp án chi tiết
Câu 1
Đáp án đúng: ʍ
\(x = 2\).
Câu 2
Đáp án đúng: ʋ
Đồ thị hàm số có điểm cực tiểu là \(\left( { - 1;3} \right)\).
Câu 3
Đáp án đúng: ʊ
\(1\).
Câu 4
Đáp án đúng: ʍ
\(\left( { - 1\,;\, - 4} \right)\)
Câu 5
Đáp án đúng: ʊ
4.
Câu 6
Đáp án đúng: ʊ
3.
Câu 7
Đáp án đúng: ʍ
\(0\).
Câu 8
Đáp án đúng: ʋ
\(2\).
Câu 9
Đáp án đúng: ʋ
\(f\) đạt cực tiểu tại \(x = - 2\).
Câu 10
Đáp án đúng: ʌ
\(7\).
