Đề Kiểm Tra Giữa Học Kì 1 Môn Toán 12 Online-Đề 1
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-kiem-tra-giua-hoc-ki-1-mon-toan-12-online-de-1
Đề Kiểm Tra: Đề Kiểm Tra Giữa Học Kì 1 Môn Toán 12 Online-Đề 1
\(m = - 6\).
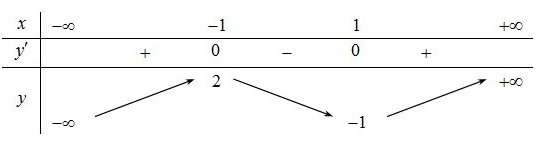 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?Hàm số đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\).
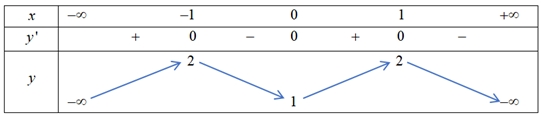 Giá trị cực tiểu của hàm số đã cho bằng
Giá trị cực tiểu của hàm số đã cho bằng\(1\).
Khối mười hai mặt đều.
 Hàm số \(y = f(x)\) nghịch biến trên khoảng nào sau đây?
Hàm số \(y = f(x)\) nghịch biến trên khoảng nào sau đây?\(( - 7;1)\).
\(3\beta h\)
Đồ thị hàm số có tiệm cận đứng là x= 1.
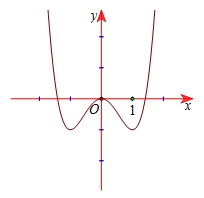
\(y = {x^4} - 2{x^2}\).
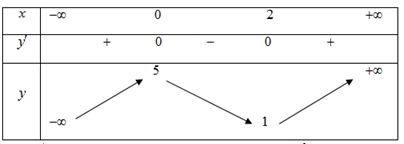
Hàm số đạt cực đại tại \(x = 5\).
\(V = \sqrt 3 {a^3}\).
14.
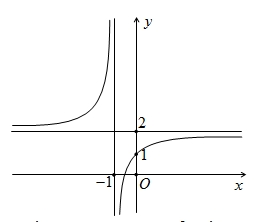
\(y = \frac{{x - 1}}{{x + 1}}\).
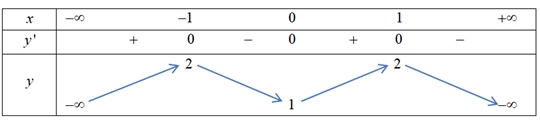 Giá trị lớn nhất của hàm số đã cho bằng
Giá trị lớn nhất của hàm số đã cho bằng\(0\).
\(V = \frac{{\sqrt 3 {a^3}}}{3}\).
8.
\(\left( { - 1;2} \right).\)
\(B\left( {1; - 2} \right).\)
\(\frac{{{a^3}\sqrt {15} }}{3}\).
\(\frac{1}{2}.\)
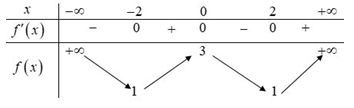 Phương trình \(f(x) – m = 0\) có 2 nghiệm phân biệt khi và chỉ khi
Phương trình \(f(x) – m = 0\) có 2 nghiệm phân biệt khi và chỉ khi\(m = 3\).
1.
Hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
\(\frac{5}{3}\).
\({a^3}\sqrt 2 \).
\(1 < m \leqslant 5\).
5.
\(m > 1\) .
\(\frac{{{a^3}\sqrt {15} }}{8}\).
\(\frac{{{a^3}\sqrt 3 }}{{12}}\).
\(\frac{{3{a^3}\sqrt {15} }}{5}\)
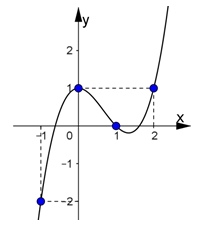 Hàm số \(g(x) = \frac{{{x^3}}}{3} – {x^2} + x – f(x) + 3\) nghịch biến trong khoảng nào sau đây:
Hàm số \(g(x) = \frac{{{x^3}}}{3} – {x^2} + x – f(x) + 3\) nghịch biến trong khoảng nào sau đây:\(\left( { - \infty ;0} \right)\).
\(10\)
