Đề Ôn Thi TN THPT Năm 2023 Môn Toán Online-Đề 13
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-on-thi-tn-thpt-nam-2023-mon-toan-online-de-13
Đề Kiểm Tra: Đề Ôn Thi TN THPT Năm 2023 Môn Toán Online-Đề 13
\(D\left( {2;2024} \right)\).
\(\frac{{32\pi \sqrt 3 }}{9}\left( {dvdt} \right)\).
\(\int {f\left( x \right){\text{d}}x = 3\sin 3x + C} \).
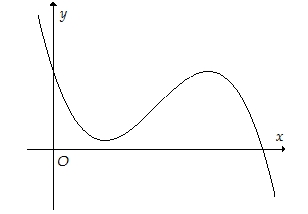 Tìm số điểm cực trị của hàm số \(y = f\left( x \right)\).
Tìm số điểm cực trị của hàm số \(y = f\left( x \right)\).\(3\).
\(S = \left( { - \infty ;2} \right)\).
\(\frac{1}{6}{a^3}\).
\(\left( {0;\frac{1}{2}} \right)\).
\(x = 8\).
\(9\).
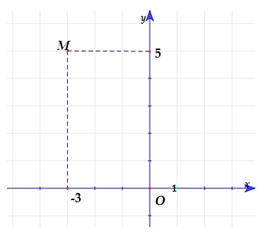
\(w = - 9 + 14i\).
\(\overrightarrow n = \left( { - 2;{\text{ }} - {\text{6; }} - {\text{10}}} \right)\).
\(M\left( { - 2;3;7} \right)\).
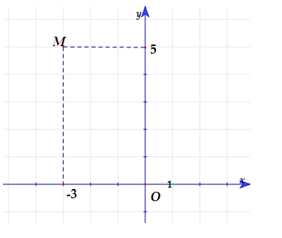
\(\overline z = - 3 - 5i\).
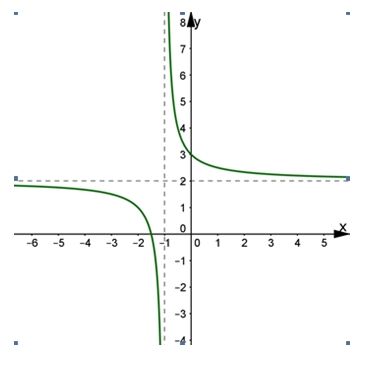
\(x = 1\) và \(y = - 2\).
\(5\).
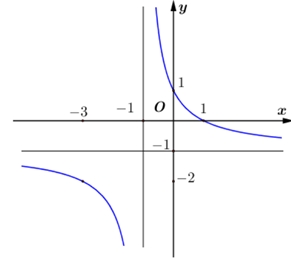
\(y = \frac{{ - x + 2}}{{x + 1}}\).
\( - 8\).
\(C_{12}^2\).
\(V = \frac{{{a^3}\sqrt 3 }}{4}\).
\(y' = \frac{{{3^{2023}}}}{{\ln 3}}\).
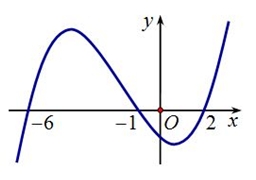
\(\left( { - 2;1} \right)\).
\(12\pi {a^2}\)
\(I = 3\).
\({u_1} = - 3\).
\(\int {f(x + 2)} \,{\text{d}}x = \frac{{{x^2}}}{4} + 2x + C\).
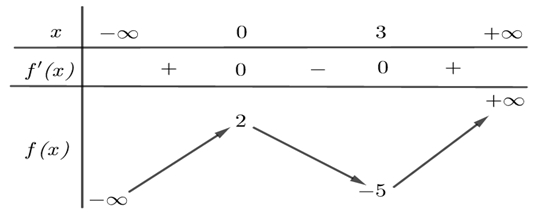 Giá trị cực tiểu của hàm số đã cho bằng
Giá trị cực tiểu của hàm số đã cho bằng\( - 5\).
\(3\)
\(y = \frac{{x - 2}}{{x - 1}}\).
\({2^{18}}\).
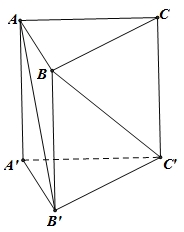
\(90^\circ \).
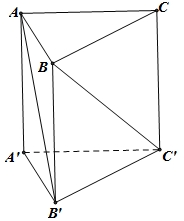 Ta có \(\overrightarrow {AB'} .\overrightarrow {BC'} = \left( {\overrightarrow {AB} + \overrightarrow {BB'} } \right)\left( {\overrightarrow {BC} + \overrightarrow {CC'} } \right)\)\( = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC'} + \overrightarrow {BB'} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {CC'} \)\( = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC'} + \overrightarrow {BB'} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {CC'} \)\( = – \frac{{{a^2}}}{2} + 0 + 0 + 2{a^2} = \frac{{3{a^2}}}{2}\).Suy ra \(\cos \left( {\overrightarrow {AB'} ,\overrightarrow {BC'} } \right) = \frac{{\overrightarrow {AB'} .\overrightarrow {BC'} }}{{\left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {BC'} } \right|}}\)\( = \frac{{\frac{{3{a^2}}}{2}}}{{a\sqrt 3 .a\sqrt 3 }} = \frac{1}{2} \Rightarrow \widehat {\left( {AB',BC'} \right)} = 60^\circ \).
Ta có \(\overrightarrow {AB'} .\overrightarrow {BC'} = \left( {\overrightarrow {AB} + \overrightarrow {BB'} } \right)\left( {\overrightarrow {BC} + \overrightarrow {CC'} } \right)\)\( = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC'} + \overrightarrow {BB'} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {CC'} \)\( = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC'} + \overrightarrow {BB'} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {CC'} \)\( = – \frac{{{a^2}}}{2} + 0 + 0 + 2{a^2} = \frac{{3{a^2}}}{2}\).Suy ra \(\cos \left( {\overrightarrow {AB'} ,\overrightarrow {BC'} } \right) = \frac{{\overrightarrow {AB'} .\overrightarrow {BC'} }}{{\left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {BC'} } \right|}}\)\( = \frac{{\frac{{3{a^2}}}{2}}}{{a\sqrt 3 .a\sqrt 3 }} = \frac{1}{2} \Rightarrow \widehat {\left( {AB',BC'} \right)} = 60^\circ \).\(\frac{{e + 1}}{2}\).
\(\left( P \right):5x + 2y + 4z - 5 = 0\).
\(P = - 1\)
\(a\)
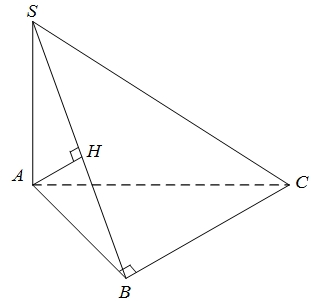 Kẻ \(AH \bot SB\) trong mặt phẳng \(\left( {SBC} \right)\)Ta có: \(\left\{ {\begin{array}{*{20}{c}} {BC \bot AB} \\ {BC \bot SA} \end{array} \Rightarrow BC \bot \left( {SAB} \right)} \right.\) \( \Rightarrow BC \bot AH\)Vậy \(\left\{ {\begin{array}{*{20}{c}} {AH \bot BC} \\ {AH \bot SB} \end{array} \Rightarrow AH \bot \left( {SBC} \right)} \right.\) \( \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AH = \frac{1}{2}SB = \frac{{a\sqrt 2 }}{2}\).
Kẻ \(AH \bot SB\) trong mặt phẳng \(\left( {SBC} \right)\)Ta có: \(\left\{ {\begin{array}{*{20}{c}} {BC \bot AB} \\ {BC \bot SA} \end{array} \Rightarrow BC \bot \left( {SAB} \right)} \right.\) \( \Rightarrow BC \bot AH\)Vậy \(\left\{ {\begin{array}{*{20}{c}} {AH \bot BC} \\ {AH \bot SB} \end{array} \Rightarrow AH \bot \left( {SBC} \right)} \right.\) \( \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AH = \frac{1}{2}SB = \frac{{a\sqrt 2 }}{2}\).\(\frac{1}{6}\).
\(\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z + 1}}{{ - 1}}\).
\(65021\).
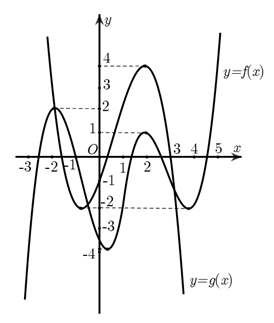 Khi đó tổng số nghiệm của hai phương trình \(f\left( {g\left( x \right)} \right) = 0\) và \(g\left( {f\left( x \right)} \right) = 0\) là
Khi đó tổng số nghiệm của hai phương trình \(f\left( {g\left( x \right)} \right) = 0\) và \(g\left( {f\left( x \right)} \right) = 0\) là\(22\).
\(\frac{{31}}{8}\).
\(\frac{{8{a^3}}}{3}\).
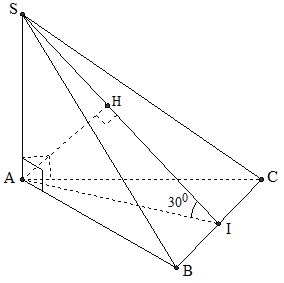 Gọi \(I\) là trung điểm sủa \(BC\) suy ra góc giữa mp\(\left( {SBC} \right)\) và mp\(\left( {ABC} \right)\) là \(\widehat {SIA} = {30^0}\).\(H\) là hình chiếu vuông góc của \(A\) trên \(SI\) suy ra \(d\left( {A,\left( {SBC} \right)} \right) = AH = a\).Xét tam giác \(AHI\) vuông tại \(H\) suy ra \(AI = \frac{{AH}}{{\sin {{30}^0}}} = 2a\).Giả sử tam giác đều \(ABC\) có cạnh bằng \(x\), mà \(AI\) là đường cao suy ra \(2a = x\frac{{\sqrt 3 }}{2} \Rightarrow x = \frac{{4a}}{{\sqrt 3 }}\).Diện tích tam giác đều \(ABC\) là \({S_{ABC}} = {\left( {\frac{{4a}}{{\sqrt 3 }}} \right)^2}.\frac{{\sqrt 3 }}{4} = \frac{{4{a^2}\sqrt 3 }}{3}\).Xét tam giác \(SAI\) vuông tại \(A\) suy ra \(SA = AI.\tan {30^0} = \frac{{2a}}{{\sqrt 3 }}\).Vậy \({V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SA = \frac{1}{3}.\frac{{4{a^2}\sqrt 3 }}{3}.\frac{{2a}}{{\sqrt 3 }} = \frac{{8{a^3}}}{9}\).
Gọi \(I\) là trung điểm sủa \(BC\) suy ra góc giữa mp\(\left( {SBC} \right)\) và mp\(\left( {ABC} \right)\) là \(\widehat {SIA} = {30^0}\).\(H\) là hình chiếu vuông góc của \(A\) trên \(SI\) suy ra \(d\left( {A,\left( {SBC} \right)} \right) = AH = a\).Xét tam giác \(AHI\) vuông tại \(H\) suy ra \(AI = \frac{{AH}}{{\sin {{30}^0}}} = 2a\).Giả sử tam giác đều \(ABC\) có cạnh bằng \(x\), mà \(AI\) là đường cao suy ra \(2a = x\frac{{\sqrt 3 }}{2} \Rightarrow x = \frac{{4a}}{{\sqrt 3 }}\).Diện tích tam giác đều \(ABC\) là \({S_{ABC}} = {\left( {\frac{{4a}}{{\sqrt 3 }}} \right)^2}.\frac{{\sqrt 3 }}{4} = \frac{{4{a^2}\sqrt 3 }}{3}\).Xét tam giác \(SAI\) vuông tại \(A\) suy ra \(SA = AI.\tan {30^0} = \frac{{2a}}{{\sqrt 3 }}\).Vậy \({V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SA = \frac{1}{3}.\frac{{4{a^2}\sqrt 3 }}{3}.\frac{{2a}}{{\sqrt 3 }} = \frac{{8{a^3}}}{9}\).\(4\).
\(d:\frac{{7x - 1}}{3} = \frac{{7y - 4}}{8} = \frac{{7z + 3}}{{ - 5}}\).
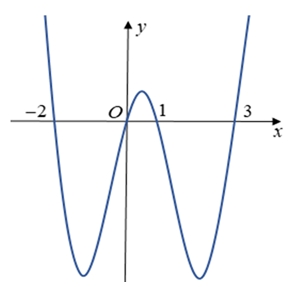 Số điểm cực tiểu của hàm số \(g\left( x \right) = \left| {f\left( x \right) – \left( {1024a + 256b + 64c + 16d + 4m + n} \right)} \right|\) là
Số điểm cực tiểu của hàm số \(g\left( x \right) = \left| {f\left( x \right) – \left( {1024a + 256b + 64c + 16d + 4m + n} \right)} \right|\) là\(7\).
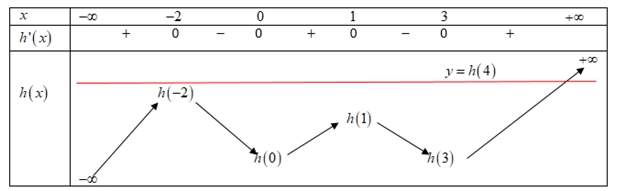 Vậy hàm số \(g\left( x \right)\) có 3 điểm cực tiểu.
Vậy hàm số \(g\left( x \right)\) có 3 điểm cực tiểu.\(\frac{{16\sqrt 6 }}{9}{a^3}\).
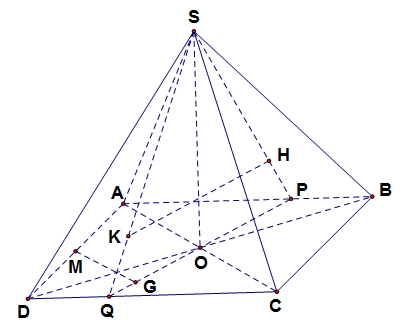 Gọi \(P,\,\,Q\) lần lượt là giao điểm của \(SH\) với \(AB\), \(SK\) với \(CD\), kẻ \(MG \bot PQ\).Vì \(HK\parallel \left( {ABCD} \right),\,\,SO \bot \left( {ABCD} \right)\) nên \(HK \bot SO\).Do tính đối xứng nên \(SO\) đi qua trung điểm của \(HK\).Mà \(SHOK\) là tứ giác nội tiếp nên \(SO\) là đường kính của đường tròn ngoại tiếp tứ giác \(SHOK\).Ta có: \(\left( {\left( {SAD} \right),\left( {ABCD} \right)} \right) = \widehat {SMO} = {45^0}\), \(SO = 2a\).\({V_{M.SHOK}} = \frac{1}{3}.MG.\frac{1}{2}.SO.HK = \frac{1}{6}.SO.MG.HK = \frac{a}{3}.MG.HK\).Để \({V_{M.SHOK}}\) lớn nhất thì \(MG.HK\) lớn nhất, khi và chỉ khi \(HK\) là đường kính của đường tròn ngoại tiếp tứ giác \(SHOK\) và \(MG = MO\).Vậy thể tích lớn nhất của khối chóp \(M.SHOK\) là: \(\frac{1}{6}.2a.2a.2a = \frac{4}{3}{a^3}\).
Gọi \(P,\,\,Q\) lần lượt là giao điểm của \(SH\) với \(AB\), \(SK\) với \(CD\), kẻ \(MG \bot PQ\).Vì \(HK\parallel \left( {ABCD} \right),\,\,SO \bot \left( {ABCD} \right)\) nên \(HK \bot SO\).Do tính đối xứng nên \(SO\) đi qua trung điểm của \(HK\).Mà \(SHOK\) là tứ giác nội tiếp nên \(SO\) là đường kính của đường tròn ngoại tiếp tứ giác \(SHOK\).Ta có: \(\left( {\left( {SAD} \right),\left( {ABCD} \right)} \right) = \widehat {SMO} = {45^0}\), \(SO = 2a\).\({V_{M.SHOK}} = \frac{1}{3}.MG.\frac{1}{2}.SO.HK = \frac{1}{6}.SO.MG.HK = \frac{a}{3}.MG.HK\).Để \({V_{M.SHOK}}\) lớn nhất thì \(MG.HK\) lớn nhất, khi và chỉ khi \(HK\) là đường kính của đường tròn ngoại tiếp tứ giác \(SHOK\) và \(MG = MO\).Vậy thể tích lớn nhất của khối chóp \(M.SHOK\) là: \(\frac{1}{6}.2a.2a.2a = \frac{4}{3}{a^3}\).\((201;202).\)
\(\frac{{\sqrt 6 }}{3}\)
\(10\).
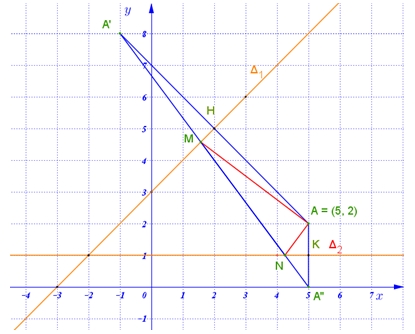 Ta có \(P = \left| {{z_1} – {z_2}} \right| + \left| {{z_1} – 5 – 2i} \right| + \left| {{z_2} – 5 – 2i} \right| = MN + MA + NA\)Gọi \(A',\,A''\)lần lượt là các điểm đối xứng với\(A\) qua các đường thẳng \({\Delta _1},\,{\Delta _2}\).Khi đó ta có \(P = MN + MA + NA = MN + MA' + NA'' \geqslant A'A''\)Dấu bằng xảy ra khi các điểm \(A',\,M,\,N,\,A''\)thẳng hàng hay \(M,N\) lần lượt là giao điểm của đường thẳng \(A'A''\) với các đường thẳng \({\Delta _1},\,{\Delta _2}\).Tính được \(A'\left( { – 1;8} \right);\,\,A''\left( {5;0} \right);\,\,A'A'' = 10\).Vậy GTNN của \(P = \left| {{z_1} – {z_2}} \right| + \left| {{z_1} – 5 – 2i} \right| + \left| {{z_2} – 5 – 2i} \right| = A'A'' = 10\).
Ta có \(P = \left| {{z_1} – {z_2}} \right| + \left| {{z_1} – 5 – 2i} \right| + \left| {{z_2} – 5 – 2i} \right| = MN + MA + NA\)Gọi \(A',\,A''\)lần lượt là các điểm đối xứng với\(A\) qua các đường thẳng \({\Delta _1},\,{\Delta _2}\).Khi đó ta có \(P = MN + MA + NA = MN + MA' + NA'' \geqslant A'A''\)Dấu bằng xảy ra khi các điểm \(A',\,M,\,N,\,A''\)thẳng hàng hay \(M,N\) lần lượt là giao điểm của đường thẳng \(A'A''\) với các đường thẳng \({\Delta _1},\,{\Delta _2}\).Tính được \(A'\left( { – 1;8} \right);\,\,A''\left( {5;0} \right);\,\,A'A'' = 10\).Vậy GTNN của \(P = \left| {{z_1} – {z_2}} \right| + \left| {{z_1} – 5 – 2i} \right| + \left| {{z_2} – 5 – 2i} \right| = A'A'' = 10\).\(\left( {1;\frac{3}{2}} \right)\).
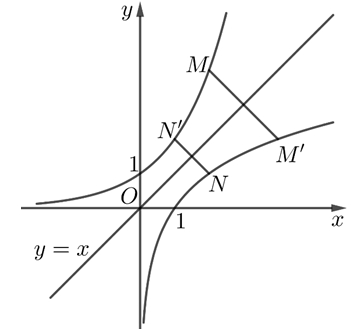 Nếu \(M \ne N'\) thì \(MM'NN'\) là hình thang cân suy ra \(MN \geqslant \min \left\{ {MM',NN'} \right\}\),do đó \(MN\) nhỏ nhất khi \(M,N\) đối xứng qua \(d\).Gọi \(\Delta \) là tiếp tuyến của \(\left( {{C_2}} \right)\) song song với \(d\) tại điểm \(I\left( {{x_0};{y_0}} \right)\).Khi \(M,N\) đối xứng nhau qua \(d\) thì \(MN = 2d\left[ {N,d} \right] \geqslant 2d\left[ {\Delta ,d} \right]\).Hệ số góc đường thẳng \(\Delta \) là \({k_\Delta } = 1\).Ta có: \(y = {2^x} \Rightarrow y' = {2^x}\ln 2\).\({k_\Delta } = 1 \Leftrightarrow {2^{{x_0}}}\ln 2 = 1 \Leftrightarrow {x_0} = – {\log _2}\left( {\ln 2} \right)\)\( \Rightarrow {y_0} = \frac{1}{{\ln 2}}\).\( \Rightarrow \left( \Delta \right):y = x + {\log _2}\left( {\ln 2} \right) + \frac{1}{{\ln 2}}\).\( \Rightarrow d\left[ {d,\Delta } \right] = \frac{{\left| {{{\log }_2}\left( {\ln 2} \right) + \frac{1}{{\ln 2}}} \right|}}{{\sqrt 2 }} \approx 0.65\)Ta có: \(M{N_{\min }} = \sqrt 2 \left| {\log \left( {\ln 2} \right) + \frac{1}{{\ln 2}}} \right| \approx 1.29\)
Nếu \(M \ne N'\) thì \(MM'NN'\) là hình thang cân suy ra \(MN \geqslant \min \left\{ {MM',NN'} \right\}\),do đó \(MN\) nhỏ nhất khi \(M,N\) đối xứng qua \(d\).Gọi \(\Delta \) là tiếp tuyến của \(\left( {{C_2}} \right)\) song song với \(d\) tại điểm \(I\left( {{x_0};{y_0}} \right)\).Khi \(M,N\) đối xứng nhau qua \(d\) thì \(MN = 2d\left[ {N,d} \right] \geqslant 2d\left[ {\Delta ,d} \right]\).Hệ số góc đường thẳng \(\Delta \) là \({k_\Delta } = 1\).Ta có: \(y = {2^x} \Rightarrow y' = {2^x}\ln 2\).\({k_\Delta } = 1 \Leftrightarrow {2^{{x_0}}}\ln 2 = 1 \Leftrightarrow {x_0} = – {\log _2}\left( {\ln 2} \right)\)\( \Rightarrow {y_0} = \frac{1}{{\ln 2}}\).\( \Rightarrow \left( \Delta \right):y = x + {\log _2}\left( {\ln 2} \right) + \frac{1}{{\ln 2}}\).\( \Rightarrow d\left[ {d,\Delta } \right] = \frac{{\left| {{{\log }_2}\left( {\ln 2} \right) + \frac{1}{{\ln 2}}} \right|}}{{\sqrt 2 }} \approx 0.65\)Ta có: \(M{N_{\min }} = \sqrt 2 \left| {\log \left( {\ln 2} \right) + \frac{1}{{\ln 2}}} \right| \approx 1.29\)
\(\left| z \right| = 1\).
\(I\left( { - 2;0;1} \right)\), \(R = 1\).
