Đề Ôn Thi TN THPT 2023 Môn Toán Online-Đề 12
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-on-thi-tn-thpt-2023-mon-toan-online-de-12
Đề Kiểm Tra: Đề Ôn Thi TN THPT 2023 Môn Toán Online-Đề 12
\(I(0; - 2; - 1)\).
\(2\).
\(\overrightarrow v = (2; - 1; - 1)\).
\(({\log _6}3; + \infty )\).
\(3{a^3}\).
\(32{a^3}\).
\(\left( {2\,;\, - 2\,;\,2} \right)\).
6.
\(y' = {3^x}\ln 3\).
\(\int {f\left( x \right){\text{d}}x = - \sin x + x + C} \).
\(4\).
\(48\pi \).
\(\int {f\left( x \right){\text{d}}x} = {x^3} + C\).
\(\left( {2; - 3} \right)\).
\({a^{\frac{1}{4}}}\).

4.
\(S = 16\pi {R^2}.\)
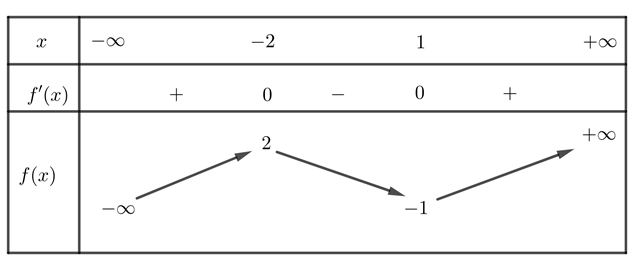
\(\left( { - \infty \,;\, - 2} \right)\).
\(1 + i\).
\(x = 11\).
\(C_n^3 = \frac{{n!}}{{3!\left( {n - 3} \right)!}}\).
\(0\).
\(\left( { - \infty ;1} \right)\).
\( - 3i\).
\(2x + 2y + z - 11 = 0\).
\(x = 2a + 3b\).
\(60^0}\).
\(3\sqrt 2 a\).
\(54\pi \).
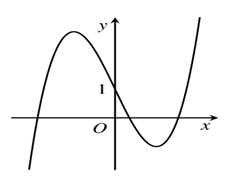
\(y = {x^3} - 3x + 1\).
\(m = 4\).
\(x - y - 3z + 9 = 0\)
\(\frac{7}{{44}}\).
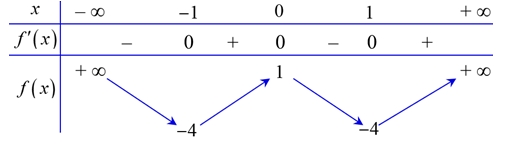 Phương trình \(2f\left( x \right) + 5 = 0\) có bao nhiêu nghiệm?
Phương trình \(2f\left( x \right) + 5 = 0\) có bao nhiêu nghiệm?\(4\).
\(y = 1\).
Vô số.
\(a\sqrt 2 \).
\(I = 4\).
\(\frac{{x - 2}}{1} = \frac{{y - 4}}{1} = \frac{{z - 1}}{1}\).
\(S = \frac{3}{4} - \frac{\pi }{4}\).
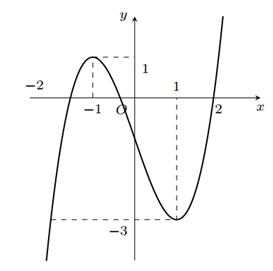
\( - 2\).
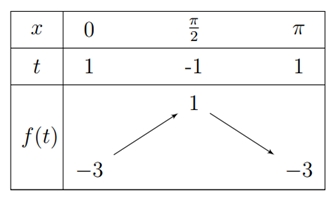 Dựa vào bảng biến thiên, yêu cầu bài toán tương đương\( – 3 \leqslant m < 1 \Rightarrow m \in \left\{ { - 3; - 2; - 1;0} \right\} \Rightarrow \sum m = - 6\).
Dựa vào bảng biến thiên, yêu cầu bài toán tương đương\( – 3 \leqslant m < 1 \Rightarrow m \in \left\{ { - 3; - 2; - 1;0} \right\} \Rightarrow \sum m = - 6\).\(\left( {3; - 12;10} \right)\).
\(\frac{{{a^3}\sqrt 7 }}{3}\).
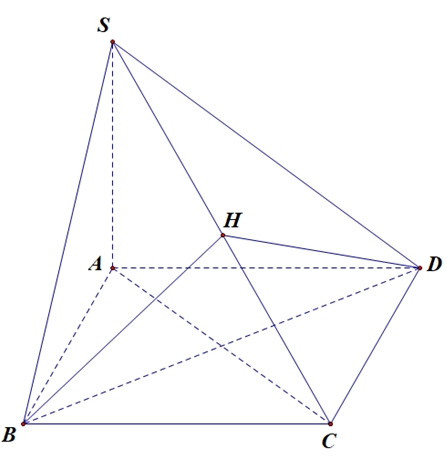 Dựng \(BH \bot SC\)\( \Rightarrow SC \bot \left( {BHD} \right) \Rightarrow SC \bot DH\)\( \Rightarrow \left( {\left( {SBC} \right),\left( {SCD} \right)} \right) = \left( {BH,DH} \right)\)TH1: \(\cos \widehat {BHD} = – \frac{9}{{16}}\)Ta có: \(BD = AC\sqrt 2 = a\sqrt 2 \) \(B{D^2} = B{H^2} + D{H^2} – 2BH \cdot DH \cdot \cos \widehat {BHD}\)Mà \(BH = DH\left( {\Delta SBC = \Delta SDC} \right)\)Nên \(B{D^2} = B{H^2} + B{H^2} – 2BH \cdot BH \cdot \frac{{ – 9}}{{16}} = \frac{{25}}{8}B{H^2}\) \( \Rightarrow B{H^2} = \frac{8}{{25}}2{a^2} \Leftrightarrow BH = \frac{4}{5}a\) \(\frac{1}{{B{H^2}}} = \frac{1}{{S{B^2}}} + \frac{1}{{B{C^2}}} \Leftrightarrow \frac{1}{{S{B^2}}} = \frac{1}{{B{H^2}}} – \frac{1}{{B{C^2}}} \Leftrightarrow SB = \frac{{BH \cdot BC}}{{\sqrt {B{C^2} – B{H^2}} }} = \frac{4}{3}a\) \(SA = \sqrt {S{B^2} – A{B^2}} = \frac{{\sqrt 7 }}{3}a\)\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SA \cdot AB \cdot AD = \frac{1}{3} \cdot \frac{{\sqrt 7 }}{3}a \cdot a \cdot a = \frac{{\sqrt 7 }}{9}{a^3}\)TH2: \(\cos \widehat {BHD} = \frac{9}{{16}}\)Ta có: \(B{D^2} = B{H^2} + D{H^2} – 2BH \cdot DH \cdot \cos \widehat {BHD} = B{H^2} + B{H^2} – 2BH \cdot BH \cdot \frac{9}{{16}} = \frac{7}{8}B{H^2}\) \( \Rightarrow B{H^2} = \frac{8}{7}2{a^2} \Leftrightarrow BH = \frac{{4\sqrt 7 }}{7}a > BC\)(vô lý)
Dựng \(BH \bot SC\)\( \Rightarrow SC \bot \left( {BHD} \right) \Rightarrow SC \bot DH\)\( \Rightarrow \left( {\left( {SBC} \right),\left( {SCD} \right)} \right) = \left( {BH,DH} \right)\)TH1: \(\cos \widehat {BHD} = – \frac{9}{{16}}\)Ta có: \(BD = AC\sqrt 2 = a\sqrt 2 \) \(B{D^2} = B{H^2} + D{H^2} – 2BH \cdot DH \cdot \cos \widehat {BHD}\)Mà \(BH = DH\left( {\Delta SBC = \Delta SDC} \right)\)Nên \(B{D^2} = B{H^2} + B{H^2} – 2BH \cdot BH \cdot \frac{{ – 9}}{{16}} = \frac{{25}}{8}B{H^2}\) \( \Rightarrow B{H^2} = \frac{8}{{25}}2{a^2} \Leftrightarrow BH = \frac{4}{5}a\) \(\frac{1}{{B{H^2}}} = \frac{1}{{S{B^2}}} + \frac{1}{{B{C^2}}} \Leftrightarrow \frac{1}{{S{B^2}}} = \frac{1}{{B{H^2}}} – \frac{1}{{B{C^2}}} \Leftrightarrow SB = \frac{{BH \cdot BC}}{{\sqrt {B{C^2} – B{H^2}} }} = \frac{4}{3}a\) \(SA = \sqrt {S{B^2} – A{B^2}} = \frac{{\sqrt 7 }}{3}a\)\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SA \cdot AB \cdot AD = \frac{1}{3} \cdot \frac{{\sqrt 7 }}{3}a \cdot a \cdot a = \frac{{\sqrt 7 }}{9}{a^3}\)TH2: \(\cos \widehat {BHD} = \frac{9}{{16}}\)Ta có: \(B{D^2} = B{H^2} + D{H^2} – 2BH \cdot DH \cdot \cos \widehat {BHD} = B{H^2} + B{H^2} – 2BH \cdot BH \cdot \frac{9}{{16}} = \frac{7}{8}B{H^2}\) \( \Rightarrow B{H^2} = \frac{8}{7}2{a^2} \Leftrightarrow BH = \frac{{4\sqrt 7 }}{7}a > BC\)(vô lý)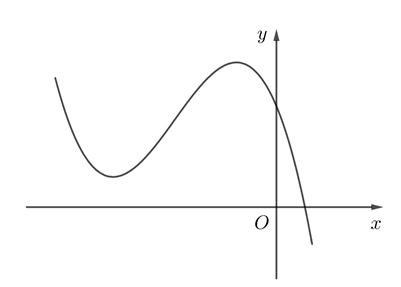
\(a > 0;b < 0;c > 0\).
\(\sqrt {53} \).
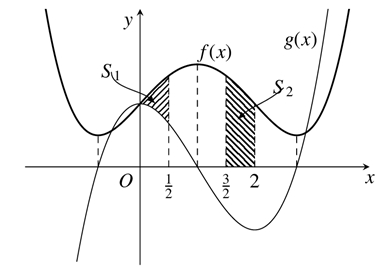
\(\frac{{791}}{{640}}\).
\(1\).
Vì \(y \in [0;2023]\) nên \({y^2} + 615 \in [615;{2023^2} + 615] \Rightarrow {2^x} \in [615;{2023^2} + 615]\).\(\begin{gathered} \Rightarrow 615 \leqslant {2^x} \leqslant {2023^2} + 615 \Rightarrow 9,28 \leqslant x \leqslant 21,9 \hfill \\ \Rightarrow x \in [10;21] \hfill \\ \end{gathered} \)
Bảng giá trị tương ứng:

Vậy ta có một cặp duy nhất thoả mãn bài toán là \(x = 12\) và \(y = 59\).
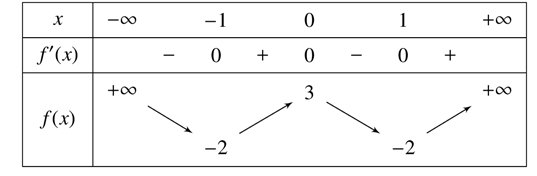
\(6\).
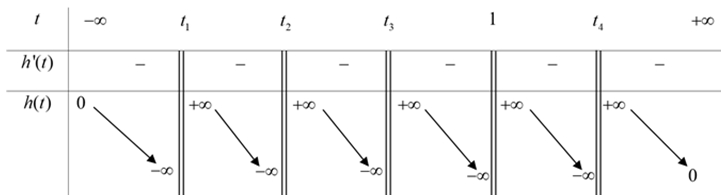 Từ bảng biến thiên ta thấy phương trình \(h\left( t \right) = 0\) luôn có 4 nghiệm đơn phân biệt do đó hàm số \(g(x)\) có 4 điểm cực trị.
Từ bảng biến thiên ta thấy phương trình \(h\left( t \right) = 0\) luôn có 4 nghiệm đơn phân biệt do đó hàm số \(g(x)\) có 4 điểm cực trị.\(\frac{{22}}{5}\).
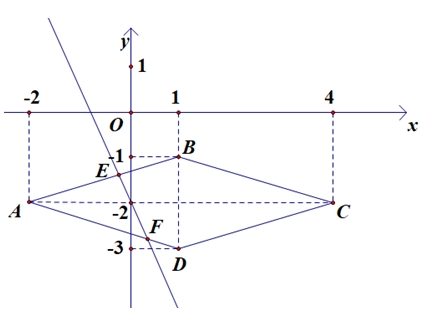 Biểu thức \(P = 2x + 3y + 5\) sẽ đạt giá trị lớn nhất và nhỏ nhất trên miền trong (tính cả biên) của ngũ giác \(EBCDF\) khi \(\left( {x;y} \right)\) là toạ độ của một trong các đỉnh \(E\left( {\frac{{ – 2}}{7};\frac{{ – 10}}{7}} \right)\); \(B\left( {1; – 1} \right)\); \(C\left( {4; – 2} \right)\); \(D\left( {1; – 3} \right)\); \(F\left( {\frac{2}{5};\frac{{ – 14}}{5}} \right)\).Ta có:
Biểu thức \(P = 2x + 3y + 5\) sẽ đạt giá trị lớn nhất và nhỏ nhất trên miền trong (tính cả biên) của ngũ giác \(EBCDF\) khi \(\left( {x;y} \right)\) là toạ độ của một trong các đỉnh \(E\left( {\frac{{ – 2}}{7};\frac{{ – 10}}{7}} \right)\); \(B\left( {1; – 1} \right)\); \(C\left( {4; – 2} \right)\); \(D\left( {1; – 3} \right)\); \(F\left( {\frac{2}{5};\frac{{ – 14}}{5}} \right)\).Ta có: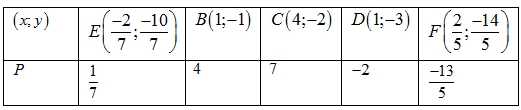 Suy ra \(M = 7;\,m = – \frac{{13}}{5} \Rightarrow M + m = \frac{{22}}{5}\).
Suy ra \(M = 7;\,m = – \frac{{13}}{5} \Rightarrow M + m = \frac{{22}}{5}\).6.
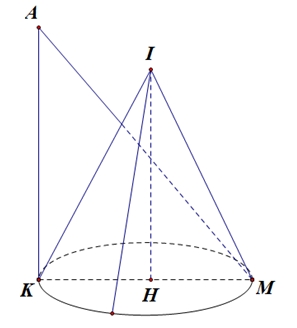 \(IH = d\left( {I,\left( P \right)} \right) = \frac{{\left| {2.2 + 2 + 5} \right|}}{3} = \frac{{11}}{3}\).Gọi \(H\)là hình chiếu vuông góc của \(I\)xuống mặt phẳng \((P) \Rightarrow H\left( {\frac{{ – 4}}{9};\frac{{11}}{9};\frac{{13}}{9}} \right)\).Gọi \(K\)là hình chiếu vuông góc của \(A\)xuống mặt phẳng \((P) \Rightarrow K\left( {\frac{{ – 26}}{9};\frac{{ – 5}}{9};\frac{{ – 1}}{9}} \right)\).Do Điểm \(M\) thay đổi thuộc mặt phẳng \((P)\) và \(IM = 5\)nên \(M\) nằm trên đường tròn tâm \(H\), bán kính \(HM = \sqrt {I{M^2} – I{H^2}} = \sqrt {{5^2} – {{\left( {\frac{{11}}{3}} \right)}^2}} = \frac{{2\sqrt {26} }}{3}\).\(\overrightarrow {HK} = \left( {\frac{{ – 22}}{9};\frac{{ – 16}}{9}; – \frac{{14}}{9}} \right) \Rightarrow HK = \frac{{2\sqrt {26} }}{3} \Rightarrow K \in \left( {H,HK} \right)\). Do đó để \(AM\)lớn nhất thì \(KM\) lớn nhất khí và chỉ khi \(M\) là điểm đối xứng với \(K\) qua \(H\). Khi đó tọa độ điểm \(M(2;3;3) \Rightarrow a = 2,b = 3,c = 3 \Rightarrow a + b + 2c = 11\).
\(IH = d\left( {I,\left( P \right)} \right) = \frac{{\left| {2.2 + 2 + 5} \right|}}{3} = \frac{{11}}{3}\).Gọi \(H\)là hình chiếu vuông góc của \(I\)xuống mặt phẳng \((P) \Rightarrow H\left( {\frac{{ – 4}}{9};\frac{{11}}{9};\frac{{13}}{9}} \right)\).Gọi \(K\)là hình chiếu vuông góc của \(A\)xuống mặt phẳng \((P) \Rightarrow K\left( {\frac{{ – 26}}{9};\frac{{ – 5}}{9};\frac{{ – 1}}{9}} \right)\).Do Điểm \(M\) thay đổi thuộc mặt phẳng \((P)\) và \(IM = 5\)nên \(M\) nằm trên đường tròn tâm \(H\), bán kính \(HM = \sqrt {I{M^2} – I{H^2}} = \sqrt {{5^2} – {{\left( {\frac{{11}}{3}} \right)}^2}} = \frac{{2\sqrt {26} }}{3}\).\(\overrightarrow {HK} = \left( {\frac{{ – 22}}{9};\frac{{ – 16}}{9}; – \frac{{14}}{9}} \right) \Rightarrow HK = \frac{{2\sqrt {26} }}{3} \Rightarrow K \in \left( {H,HK} \right)\). Do đó để \(AM\)lớn nhất thì \(KM\) lớn nhất khí và chỉ khi \(M\) là điểm đối xứng với \(K\) qua \(H\). Khi đó tọa độ điểm \(M(2;3;3) \Rightarrow a = 2,b = 3,c = 3 \Rightarrow a + b + 2c = 11\).