Đề Ôn Thi TN THPT Năm 2023 Toán Online-Đề 14
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-on-thi-tn-thpt-nam-2023-toan-online-de-14
Đề Kiểm Tra: Đề Ôn Thi TN THPT Năm 2023 Toán Online-Đề 14
\(y = - 2x + 1\).
\(\left( {1;4;3} \right)\).
\(\frac{{{x^m}}}{{{y^n}}} = {\left( {\frac{x}{y}} \right)^{m - n}}\).
\(2{x^2}\).
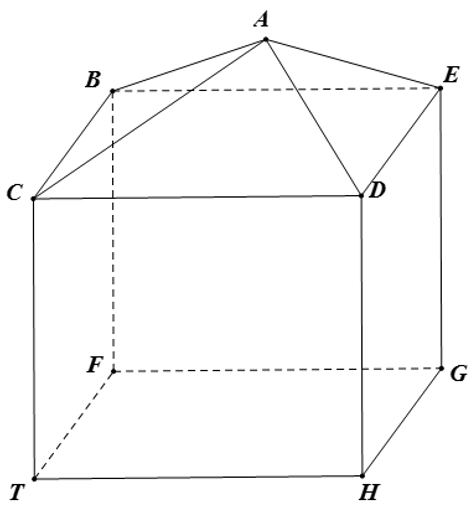
\(16\).
\(\frac{1}{{{a^{2016}}}} < \frac{1}{{{a^{2017}}}}\).
\(\left( {5;\, + \infty } \right)\).
\(1\).
\(\frac{{Bh}}{3}\).
\(x = 2\).
\(x = 1\); \(x = - 2\).
\(3\left( {3x + 1} \right){e^{3x + 1}}\).
\(20\pi {a^2}\).
\(m = 1\).
\(70\pi \left( {c{m^2}} \right)\).
\(P = \frac{3}{2}\).
\(\sin x + {2^x}\ln 2 + C\).
\({150^0}\).
2625.
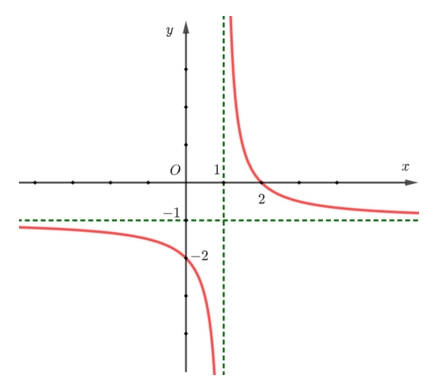
\(T = 6\).
\(\mathbb{R}\).
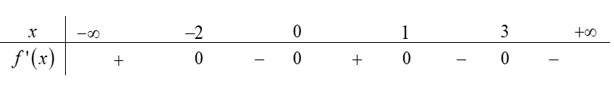 Hàm số đã cho đạt cực tiểu tại điểm nào sau đây?
Hàm số đã cho đạt cực tiểu tại điểm nào sau đây?\(x = 1\).
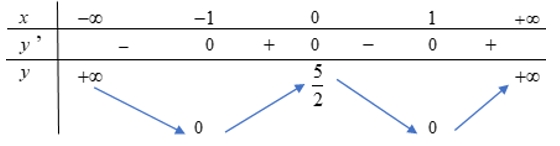 Hàm số \(y = f(x)\)nghịch biến trên khoảng nào sau đây?
Hàm số \(y = f(x)\)nghịch biến trên khoảng nào sau đây?\(( - \infty ; - 2)\).
\(S = 12\pi {a^2}\).
\(5\).
\(2\).
\(\frac{{a\sqrt 3 }}{2}\).
\(V = 2\sqrt 3 \pi \).
\(6\).
\(S = \left( { - \infty ;1} \right]\).
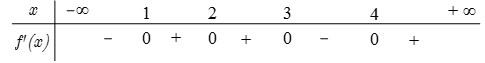 Hàm số \(y = f\left( {2x + 1} \right) – 4{x^3} + 9{x^2} – 6x\) đồng biến trên khoảng nào dưới đây?
Hàm số \(y = f\left( {2x + 1} \right) – 4{x^3} + 9{x^2} – 6x\) đồng biến trên khoảng nào dưới đây?\(\left( {1\,;\,3} \right)\).
\(2\).
\(1007\).
 Từ bảng biến thiên suy ra \(\left[ \begin{gathered} m < 5 \hfill \\ m = 9 \hfill \\ \end{gathered} \right.\) là các giá trị thoả mãn yêu cầu bài toán.Do \(\left\{ \begin{gathered} m \in \left( { - 1000\,;\,1000} \right) \hfill \\ m \in \mathbb{Z} \hfill \\ \end{gathered} \right.\) nên có \(1005\) giá trị của \(m\) tìm được.
Từ bảng biến thiên suy ra \(\left[ \begin{gathered} m < 5 \hfill \\ m = 9 \hfill \\ \end{gathered} \right.\) là các giá trị thoả mãn yêu cầu bài toán.Do \(\left\{ \begin{gathered} m \in \left( { - 1000\,;\,1000} \right) \hfill \\ m \in \mathbb{Z} \hfill \\ \end{gathered} \right.\) nên có \(1005\) giá trị của \(m\) tìm được.\(4\).
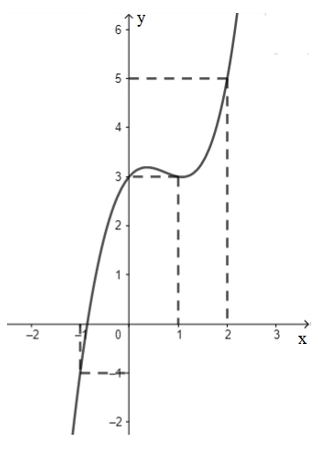
\(g\left( { - 1} \right) > g\left( 1 \right)\).
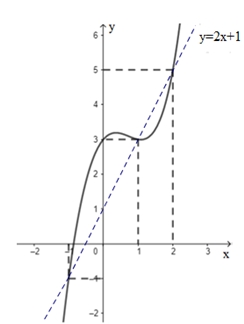 Do đó: \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = – 1 \hfill \\ x = 1 \hfill \\ x = 2 \hfill \\ \end{gathered} \right.\). Ta có bảng biến thiên:
Do đó: \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = – 1 \hfill \\ x = 1 \hfill \\ x = 2 \hfill \\ \end{gathered} \right.\). Ta có bảng biến thiên: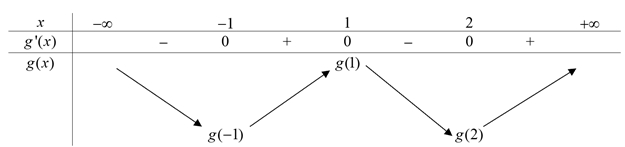 Từ BBT suy ra \(g\left( 1 \right) > g\left( 2 \right)\).
Từ BBT suy ra \(g\left( 1 \right) > g\left( 2 \right)\).\(2026\).
\(\frac{V}{{12}}\).
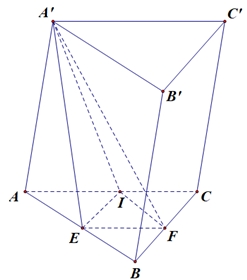 Tam giác \(ABC\) đều và \(AE = BF = CI\) nên \(\Delta AEI = \Delta BFE = \Delta CIF\) suy ra \({S_{\Delta AEI}} = {S_{\Delta BEF}} = {S_{\Delta CFI}}\).Ta có: \(\frac{{{V_{A'.EFI}}}}{V} = \frac{1}{3}.\frac{{{S_{\Delta EFI}}}}{{{S_{\Delta ABC}}}}\).Gọi cạnh của tam giác \(ABC\) là \(a\) \(\left( {a > 0} \right)\), \(AE = BF = CI = x\,\,\left( {0 \leqslant x \leqslant a} \right)\).Khi đó: \(\frac{{{S_{\Delta AEI}}}}{{{S_{\Delta ABC}}}} = \frac{{AE}}{{AB}}.\frac{{AI}}{{AC}} = \frac{{x\left( {a – x} \right)}}{{{a^2}}}\) \( \Leftrightarrow {S_{\Delta AEI}} = \frac{{x\left( {a – x} \right)}}{{{a^2}}}.{S_{\Delta ABC}}\).Suy ra: \({S_{\Delta EFI}} = {S_{\Delta ABC}} – 3.{S_{\Delta AEI}} = \frac{{{a^2} – 3ax + 3{x^2}}}{{{a^2}}}.{S_{\Delta ABC}} \Leftrightarrow \frac{{{S_{\Delta EFI}}}}{{{S_{\Delta ABC}}}} = \frac{{{a^2} – 3ax + 3{x^2}}}{{{a^2}}}\)Vậy \(\frac{{{V_{A'.EFI}}}}{V} = \frac{1}{3}.\frac{{{S_{\Delta EFI}}}}{{{S_{\Delta ABC}}}} = \frac{1}{3}.\frac{{{a^2} – 3ax + 3{x^2}}}{{{a^2}}} \Leftrightarrow {V_{A'.EFI}} = \frac{1}{3}.\frac{{{a^2} – 3ax + 3{x^2}}}{{{a^2}}}.V\).\({V_{A'.EFI}}\) đạt giá trị nhỏ nhất khi và chỉ khi biểu thức \({a^2} – 3ax + 3{x^2}\) đạt giá trị nhỏ nhất trên \(\left[ {0;a} \right]\)Ta có: \(\mathop {\min }\limits_{\left[ {0;a} \right]} \left( {{a^2} – 3ax + 3{x^2}} \right) = \frac{{{a^2}}}{4}\) khi \(x = \frac{a}{2}\).Vậy giá trị nhỏ nhất của \({V_{A'.EFI}}\) là \(\frac{V}{{12}}\).
Tam giác \(ABC\) đều và \(AE = BF = CI\) nên \(\Delta AEI = \Delta BFE = \Delta CIF\) suy ra \({S_{\Delta AEI}} = {S_{\Delta BEF}} = {S_{\Delta CFI}}\).Ta có: \(\frac{{{V_{A'.EFI}}}}{V} = \frac{1}{3}.\frac{{{S_{\Delta EFI}}}}{{{S_{\Delta ABC}}}}\).Gọi cạnh của tam giác \(ABC\) là \(a\) \(\left( {a > 0} \right)\), \(AE = BF = CI = x\,\,\left( {0 \leqslant x \leqslant a} \right)\).Khi đó: \(\frac{{{S_{\Delta AEI}}}}{{{S_{\Delta ABC}}}} = \frac{{AE}}{{AB}}.\frac{{AI}}{{AC}} = \frac{{x\left( {a – x} \right)}}{{{a^2}}}\) \( \Leftrightarrow {S_{\Delta AEI}} = \frac{{x\left( {a – x} \right)}}{{{a^2}}}.{S_{\Delta ABC}}\).Suy ra: \({S_{\Delta EFI}} = {S_{\Delta ABC}} – 3.{S_{\Delta AEI}} = \frac{{{a^2} – 3ax + 3{x^2}}}{{{a^2}}}.{S_{\Delta ABC}} \Leftrightarrow \frac{{{S_{\Delta EFI}}}}{{{S_{\Delta ABC}}}} = \frac{{{a^2} – 3ax + 3{x^2}}}{{{a^2}}}\)Vậy \(\frac{{{V_{A'.EFI}}}}{V} = \frac{1}{3}.\frac{{{S_{\Delta EFI}}}}{{{S_{\Delta ABC}}}} = \frac{1}{3}.\frac{{{a^2} – 3ax + 3{x^2}}}{{{a^2}}} \Leftrightarrow {V_{A'.EFI}} = \frac{1}{3}.\frac{{{a^2} – 3ax + 3{x^2}}}{{{a^2}}}.V\).\({V_{A'.EFI}}\) đạt giá trị nhỏ nhất khi và chỉ khi biểu thức \({a^2} – 3ax + 3{x^2}\) đạt giá trị nhỏ nhất trên \(\left[ {0;a} \right]\)Ta có: \(\mathop {\min }\limits_{\left[ {0;a} \right]} \left( {{a^2} – 3ax + 3{x^2}} \right) = \frac{{{a^2}}}{4}\) khi \(x = \frac{a}{2}\).Vậy giá trị nhỏ nhất của \({V_{A'.EFI}}\) là \(\frac{V}{{12}}\).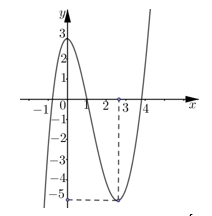 Phương trình \(f\left( {f\left( x \right) – 2} \right) = 0\) có tất cả bao nhiêu nghiệm thực phân biệt.
Phương trình \(f\left( {f\left( x \right) – 2} \right) = 0\) có tất cả bao nhiêu nghiệm thực phân biệt.\(6\).
\(\frac{{15}}{{16}}\).
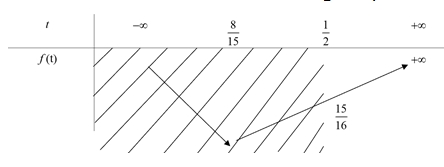 Qua bảng biến thiên ta có \(\mathop {\min }\limits_{t \in \left[ {\frac{1}{2}; + \infty } \right]} f\left( t \right) = f\left( {\frac{1}{2}} \right) = \frac{{15}}{{16}}\).Tức là, \(A \geqslant \frac{{15}}{{16}}\), dấu “=” xảy ra khi \(x = y = \frac{1}{2}\).Vậy giá trị nhỏ nhất của \(A\) bằng \(\frac{{15}}{{16}}\).
Qua bảng biến thiên ta có \(\mathop {\min }\limits_{t \in \left[ {\frac{1}{2}; + \infty } \right]} f\left( t \right) = f\left( {\frac{1}{2}} \right) = \frac{{15}}{{16}}\).Tức là, \(A \geqslant \frac{{15}}{{16}}\), dấu “=” xảy ra khi \(x = y = \frac{1}{2}\).Vậy giá trị nhỏ nhất của \(A\) bằng \(\frac{{15}}{{16}}\).\(6\).
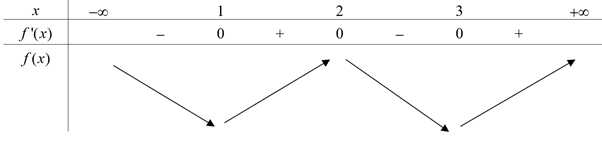 Dựa vào bảng biến thiên suy ra hàm số có 3 điểm cực trị dương.
Dựa vào bảng biến thiên suy ra hàm số có 3 điểm cực trị dương.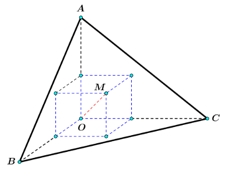
\(8c{m^3}.\)
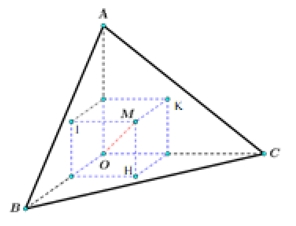 Gọi \(I,H,K\) lần lượt là hình chiếu của điểm \(M\) lên mp\(\left( {OAB} \right),\left( {OBC} \right),\left( {OCA} \right)\)Ta có \({V_{O.ABC}} = {V_{M.OAB}} + {V_{M.OBC}} + {V_{M.OCA}}\)\( \Leftrightarrow \frac{1}{6}.OA.OB.OC = \frac{1}{6}.MI.OA.OB + \frac{1}{6}.MI.OB.OC + \frac{1}{6}.MI.OC.OA\)\( \Leftrightarrow MI + 4MH + 2MK = 12\)Khi đó thể tích khối hộp chữ nhật \(V = MI.MH.MK = \frac{1}{8}MI.\left( {4MH} \right).\left( {2MK} \right)\)\( \Leftrightarrow V \leqslant \frac{1}{8}{\left( {\frac{{MI + 4MH + 2MK}}{3}} \right)^3}\) \( \Leftrightarrow V \leqslant \frac{1}{8}{.4^3} \Leftrightarrow V \leqslant 8\)Vậy \({V_{\max }} = 8\) khi \(MI = 4MH = 2MK \Leftrightarrow MI = 1cm,MH = 4cm,MK = 2cm.\)
Gọi \(I,H,K\) lần lượt là hình chiếu của điểm \(M\) lên mp\(\left( {OAB} \right),\left( {OBC} \right),\left( {OCA} \right)\)Ta có \({V_{O.ABC}} = {V_{M.OAB}} + {V_{M.OBC}} + {V_{M.OCA}}\)\( \Leftrightarrow \frac{1}{6}.OA.OB.OC = \frac{1}{6}.MI.OA.OB + \frac{1}{6}.MI.OB.OC + \frac{1}{6}.MI.OC.OA\)\( \Leftrightarrow MI + 4MH + 2MK = 12\)Khi đó thể tích khối hộp chữ nhật \(V = MI.MH.MK = \frac{1}{8}MI.\left( {4MH} \right).\left( {2MK} \right)\)\( \Leftrightarrow V \leqslant \frac{1}{8}{\left( {\frac{{MI + 4MH + 2MK}}{3}} \right)^3}\) \( \Leftrightarrow V \leqslant \frac{1}{8}{.4^3} \Leftrightarrow V \leqslant 8\)Vậy \({V_{\max }} = 8\) khi \(MI = 4MH = 2MK \Leftrightarrow MI = 1cm,MH = 4cm,MK = 2cm.\)\(30^\circ \)
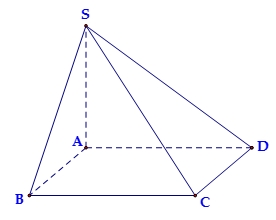
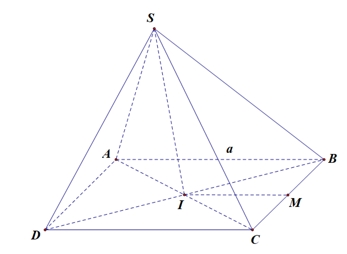 Ta có \(V = \frac{1}{3}{S_{ABCD}}.SI \Leftrightarrow SI = \frac{{3V}}{{{S_{ABCD}}}} = \frac{{3.\frac{{{a^3}}}{{2\sqrt 3 }}}}{{{a^2}}} = \frac{{a\sqrt 3 }}{2}\).Gọi \(M\) là trung điểm \(BC \Rightarrow IM = \frac{a}{2}\).Ta có: \(\left( {\left( {SBC} \right),\left( {ABCD} \right)} \right) = \left( {SM,IM} \right) = \widehat {SMI}\).Lại có \(\tan \widehat {SMI} = \frac{{SI}}{{IM}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\frac{a}{2}}} = \sqrt 3 \Rightarrow \widehat {SMI} = 60^\circ \).$$
Ta có \(V = \frac{1}{3}{S_{ABCD}}.SI \Leftrightarrow SI = \frac{{3V}}{{{S_{ABCD}}}} = \frac{{3.\frac{{{a^3}}}{{2\sqrt 3 }}}}{{{a^2}}} = \frac{{a\sqrt 3 }}{2}\).Gọi \(M\) là trung điểm \(BC \Rightarrow IM = \frac{a}{2}\).Ta có: \(\left( {\left( {SBC} \right),\left( {ABCD} \right)} \right) = \left( {SM,IM} \right) = \widehat {SMI}\).Lại có \(\tan \widehat {SMI} = \frac{{SI}}{{IM}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\frac{a}{2}}} = \sqrt 3 \Rightarrow \widehat {SMI} = 60^\circ \).$$\(357350000\) đồng.
\(\frac{{2R\sqrt 2 }}{{\sqrt 3 }}\).
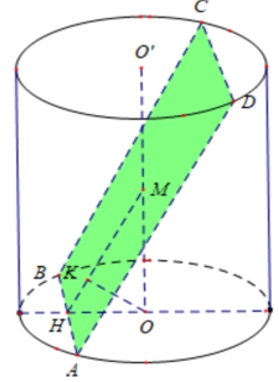 Gọi M là trung điểm của OO'. Gọi A,B là giao điểm của mặt phẳng \((\alpha )\) và đường tròn (O) và H là hình chiếu của O trên AB\( = > AB \bot (MHO)\)Trong mặt phẳng (MHO) kẻ \(OK \bot MH,(K \in MH)\) khi đó góc giữa OO' và mặt phẳng \((\alpha )\)là góc \(\widehat {OMK} = {30^0}\)Xét tam giác vuông MHO, ta có: \(HO = OM\tan {30^0} = R\tan {30^0} = \frac{{R\sqrt 3 }}{3}\)Xét tam giác vuông AHO, ta có: \(AH = \sqrt {O{A^2} – O{H^2}} = \sqrt {{R^2} – \frac{{{R^2}}}{3}} = \frac{{R\sqrt 2 }}{{\sqrt 3 }}\)Do H là trung điểm của AB nên \(AB = \frac{{2R\sqrt 2 }}{{\sqrt 3 }}\)
Gọi M là trung điểm của OO'. Gọi A,B là giao điểm của mặt phẳng \((\alpha )\) và đường tròn (O) và H là hình chiếu của O trên AB\( = > AB \bot (MHO)\)Trong mặt phẳng (MHO) kẻ \(OK \bot MH,(K \in MH)\) khi đó góc giữa OO' và mặt phẳng \((\alpha )\)là góc \(\widehat {OMK} = {30^0}\)Xét tam giác vuông MHO, ta có: \(HO = OM\tan {30^0} = R\tan {30^0} = \frac{{R\sqrt 3 }}{3}\)Xét tam giác vuông AHO, ta có: \(AH = \sqrt {O{A^2} – O{H^2}} = \sqrt {{R^2} – \frac{{{R^2}}}{3}} = \frac{{R\sqrt 2 }}{{\sqrt 3 }}\)Do H là trung điểm của AB nên \(AB = \frac{{2R\sqrt 2 }}{{\sqrt 3 }}\)\(V = 110,525\pi \),
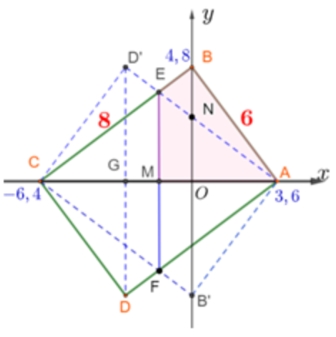 Gắn trục tọa độ Oxy như hình vẽAC=Ox, OB=OyGọi B',D' lần lượt là điểm đối xứng của B, D qua Ox, và M là trung điểm AC. Gọi E là giao điểm của AD' và CB, F là giao điểm của AD và CB'Khi cho hình chữ nhật quay xung quanh AC(Ox) thì thu được 1 khối tròn xoay chính là do hình đa giác ABED'C quay quanh trục hoành.Gọi M là trung điểm của AC. Do tính đối xứng của đa giác ABED'C nên thể tích khối tròn xoay đang xét gấp 2 lần thể tích khối tròn xoay tạo được khi quay tứ giác ABEM quanh Ox(AM)Ta có:\(OA = \frac{{A{B^2}}}{{AC}} = 3,6 = > OB = – 6,4;OB = \frac{{BA.BC}}{{AC}} = 4,8;OM = MA – OA = 5 – 3,6 = 1,4\)Ta có:\(\begin{gathered} A(3,6;0),B(0;4,8),C( – 6,4;0) \hfill \\ = > AB:y = – \frac{{OB}}{{OA}}(x – {x_A}) + {y_A} = – \frac{4}{3}(x – 3,6) \hfill \\ CB:y = \frac{{OB}}{{OC}}(x – {x_C}) + {y_C} = \frac{{4,8}}{{6,4}}(x + 6,4) = \frac{3}{4}(x + 6,4) \hfill \\ \end{gathered} \)Do đó thể tích khối tròn xoay đã cho bằng\(V = 2\left[ {\pi \int\limits_{ – 1,4}^0 {{{\left[ {\frac{3}{4}(x + 6,4)} \right]}^2}dx + \pi \int\limits_0^{3,6} {{{\left[ { – \frac{4}{3}(x – 3,6)} \right]}^2}dx} } } \right] = \frac{{4269\pi }}{{40}}\)
Gắn trục tọa độ Oxy như hình vẽAC=Ox, OB=OyGọi B',D' lần lượt là điểm đối xứng của B, D qua Ox, và M là trung điểm AC. Gọi E là giao điểm của AD' và CB, F là giao điểm của AD và CB'Khi cho hình chữ nhật quay xung quanh AC(Ox) thì thu được 1 khối tròn xoay chính là do hình đa giác ABED'C quay quanh trục hoành.Gọi M là trung điểm của AC. Do tính đối xứng của đa giác ABED'C nên thể tích khối tròn xoay đang xét gấp 2 lần thể tích khối tròn xoay tạo được khi quay tứ giác ABEM quanh Ox(AM)Ta có:\(OA = \frac{{A{B^2}}}{{AC}} = 3,6 = > OB = – 6,4;OB = \frac{{BA.BC}}{{AC}} = 4,8;OM = MA – OA = 5 – 3,6 = 1,4\)Ta có:\(\begin{gathered} A(3,6;0),B(0;4,8),C( – 6,4;0) \hfill \\ = > AB:y = – \frac{{OB}}{{OA}}(x – {x_A}) + {y_A} = – \frac{4}{3}(x – 3,6) \hfill \\ CB:y = \frac{{OB}}{{OC}}(x – {x_C}) + {y_C} = \frac{{4,8}}{{6,4}}(x + 6,4) = \frac{3}{4}(x + 6,4) \hfill \\ \end{gathered} \)Do đó thể tích khối tròn xoay đã cho bằng\(V = 2\left[ {\pi \int\limits_{ – 1,4}^0 {{{\left[ {\frac{3}{4}(x + 6,4)} \right]}^2}dx + \pi \int\limits_0^{3,6} {{{\left[ { – \frac{4}{3}(x – 3,6)} \right]}^2}dx} } } \right] = \frac{{4269\pi }}{{40}}\)\(3\).
\(V = \frac{{16\pi }}{3}\).
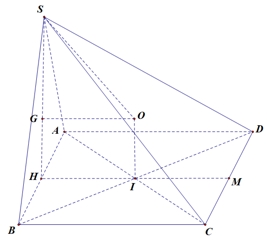 Gọi \(H,I,M,O\) lần lươt là trung điểm của \(AB,AC,CD,SM\).Ta có \(\left\{ \begin{gathered} \left( {SAB} \right) \bot \left( {ABCD} \right) \hfill \\ SH \bot AB \hfill \\ SH \subset \left( {SAB} \right) \hfill \\ \left( {SAB} \right) \cap \left( {ABCD} \right) = AB \hfill \\ \end{gathered} \right. \Rightarrow SH \bot \left( {ABCD} \right)\).Gọi \(G\) là trọng tâm tam giác \(SAB\), kẻ đường thẳng \(\Delta \) qua \(I\) và vuông góc với \(\left( {ABCD} \right)\), kẻ đường thẳng \(d\) qua \(G\) song song với \(HI\) cắt \(\Delta \) tại \(O\).Suy ra \(O\)là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\), \(R\) là bán kính mặt cầu ngoai tiếp hình chóp \(S.ABCD\). Ta có \(SH = AB.\frac{{\sqrt 3 }}{2} = \frac{{3\sqrt 3 }}{2};HI = 1\).Ta có \(R = SO = \sqrt {S{G^2} + G{O^2}} = 2\).Thể tích khối cầu \(V = \frac{4}{3}\pi {R^3} = \frac{{32}}{3}\pi \).
Gọi \(H,I,M,O\) lần lươt là trung điểm của \(AB,AC,CD,SM\).Ta có \(\left\{ \begin{gathered} \left( {SAB} \right) \bot \left( {ABCD} \right) \hfill \\ SH \bot AB \hfill \\ SH \subset \left( {SAB} \right) \hfill \\ \left( {SAB} \right) \cap \left( {ABCD} \right) = AB \hfill \\ \end{gathered} \right. \Rightarrow SH \bot \left( {ABCD} \right)\).Gọi \(G\) là trọng tâm tam giác \(SAB\), kẻ đường thẳng \(\Delta \) qua \(I\) và vuông góc với \(\left( {ABCD} \right)\), kẻ đường thẳng \(d\) qua \(G\) song song với \(HI\) cắt \(\Delta \) tại \(O\).Suy ra \(O\)là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\), \(R\) là bán kính mặt cầu ngoai tiếp hình chóp \(S.ABCD\). Ta có \(SH = AB.\frac{{\sqrt 3 }}{2} = \frac{{3\sqrt 3 }}{2};HI = 1\).Ta có \(R = SO = \sqrt {S{G^2} + G{O^2}} = 2\).Thể tích khối cầu \(V = \frac{4}{3}\pi {R^3} = \frac{{32}}{3}\pi \).2019.
\(\frac{5}{{21}}\).
\( - 4\).
