Đề Luyện Thi TN THPT 2023 Môn Toán Online-Đề 11
Ghi chú: Bạn có thể xem thêm phiên bản đầy đủ của đề thi này và các tài liệu liên quan tại đường dẫn:https://tusach.vn/tai-lieu-hoc-tap/trac-nghiem/de-luyen-thi-tn-thpt-2023-mon-toan-online-de-11
Đề Kiểm Tra: Đề Luyện Thi TN THPT 2023 Môn Toán Online-Đề 11
\(\left| z \right| = 34\).
\(R = 4\sqrt 2 \).
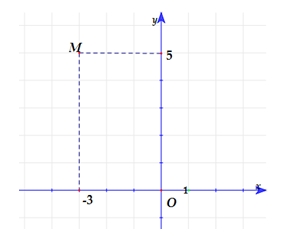
Điểm \(N(1; - 2)\).
\(\frac{{32\pi {a^3}}}{3}\).
\(\frac{1}{2}\ln \left| {2x + 3} \right| + C\).
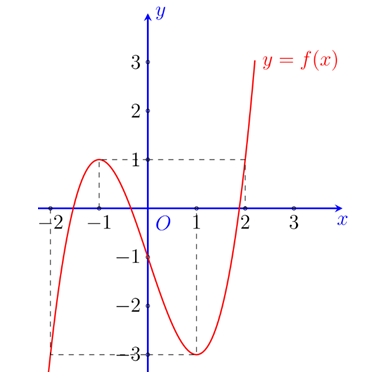
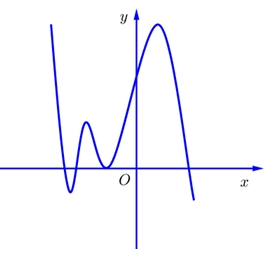 Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?\(3\).
\(\left[ { - 1; + \infty } \right)\).
\(h = \sqrt 3 a.\)
\(D = \left( { - \infty ; - 3} \right) \cup \left( {1; + \infty } \right)\).
\(\left[ \begin{gathered} x = 10 \hfill \\ x = 9 \hfill \\ \end{gathered} \right.\).
\(I = - 2\).
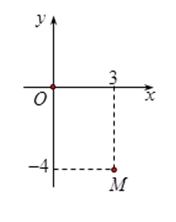
\(w = 15 - 20i\).
\(\left( {3; - 1;0} \right)\).
\(\vec d\left( { - 7;0;4} \right)\)
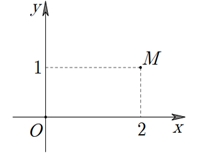
\(1 - 2i\).
\(y = - 2\).
\(P = 13\)
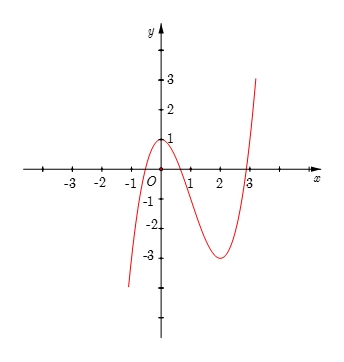
\(y = {x^3} - 3{x^2} + 1\).
\(\overrightarrow {{u_4}} = \left( { - 2;4;3} \right)\).
\(A_4^2 + A_6^1\).
\(\frac{{{a^3}}}{{12}}\).
\(y' = \frac{{2x\ln 2}}{{{x^2} + 1}}\).
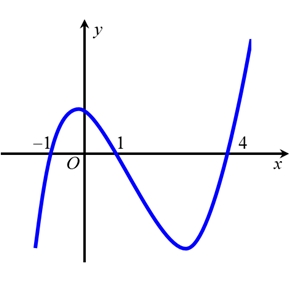 Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?\(\left( {2; + \infty } \right)\).
\(S = 3\pi {a^2}\).
\(\int\limits_3^5 {2f\left( z \right)} {\text{d}}z = 13\).
\({u_1} = \frac{1}{9}\).
\(\int {f\left( x \right){\text{d}}x} = 2{\sin ^2}2x + 2\ln x + C\).
\(y = - 3\).
\(x = 2\).
\(y = {x^4} - 3{x^2} + 5\).
\(a = 6b\).
\(90^\circ \).
\(S = \frac{3}{4}\).
\(\left( P \right):2x + y - 6 = 0\).
\(6\)
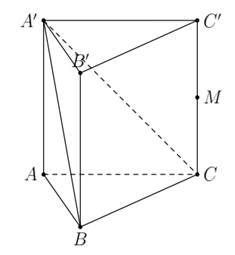
\(\frac{{\sqrt {57} a}}{{19}}\).
\(\frac{4}{9}\).
\(\left\{ \begin{gathered} x = 3 + t \hfill \\ y = 1 + 2t \hfill \\ z = - t \hfill \\ \end{gathered} \right.\).
\(10000\).
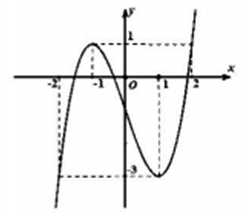
\(5\).
\( - \frac{{21}}{8}\).
\(V = \frac{{{a^3}\sqrt 6 }}{{16}}\).
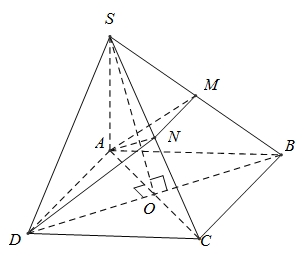 Gọi \(O = AC \cap BD\).\(AO \bot BD \Rightarrow SO \bot BD\). Nên góc của \(\left( {SBD} \right)\) và \(ABCD\) là góc \(\widehat {SOA} = {60^0}\).\({V_{S.ADN}} = \frac{1}{2}.{V_{S.ADC}} = \frac{1}{4}.{V_{S.ABCD}}\) và \({V_{S.AMN}} = \frac{1}{2}.\frac{1}{2}{V_{S.ABC}} = \frac{1}{8}{V_{S.ABCD}}\).\( \Rightarrow {V_{S.ADMN}} = {V_{S.ADN}} + {V_{S.AMN}} = \frac{3}{8}{V_{S.ABCD}}\).\(SA = AO.\tan \widehat {SOA} = \frac{{a\sqrt 2 }}{2}\tan {60^0} = \frac{{a\sqrt 6 }}{2}\) \( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SA = \frac{{{a^3}\sqrt 6 }}{6}\).\( \Rightarrow {V_{S.ADMN}} = \frac{3}{8}.\frac{{{a^3}\sqrt 6 }}{6} = \frac{{{a^3}\sqrt 6 }}{{16}}\).
Gọi \(O = AC \cap BD\).\(AO \bot BD \Rightarrow SO \bot BD\). Nên góc của \(\left( {SBD} \right)\) và \(ABCD\) là góc \(\widehat {SOA} = {60^0}\).\({V_{S.ADN}} = \frac{1}{2}.{V_{S.ADC}} = \frac{1}{4}.{V_{S.ABCD}}\) và \({V_{S.AMN}} = \frac{1}{2}.\frac{1}{2}{V_{S.ABC}} = \frac{1}{8}{V_{S.ABCD}}\).\( \Rightarrow {V_{S.ADMN}} = {V_{S.ADN}} + {V_{S.AMN}} = \frac{3}{8}{V_{S.ABCD}}\).\(SA = AO.\tan \widehat {SOA} = \frac{{a\sqrt 2 }}{2}\tan {60^0} = \frac{{a\sqrt 6 }}{2}\) \( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SA = \frac{{{a^3}\sqrt 6 }}{6}\).\( \Rightarrow {V_{S.ADMN}} = \frac{3}{8}.\frac{{{a^3}\sqrt 6 }}{6} = \frac{{{a^3}\sqrt 6 }}{{16}}\).\(2.\)
\(\frac{{x - 1}}{2} = \,\frac{{y + 1}}{1}\, = \,\frac{{z - 3}}{3}\).
\(V = \frac{{120{a^3}}}{{27}}\).
Dấu bằng xảy ra khi: \(DA = DE\) và $ BAC=900
 Hàm số \(g\left( x \right) = \left| {f\left( {xf\left( x \right)} \right) + \frac{3}{4}} \right|\) có bao nhiêu điểm cực trị?
Hàm số \(g\left( x \right) = \left| {f\left( {xf\left( x \right)} \right) + \frac{3}{4}} \right|\) có bao nhiêu điểm cực trị?\(15\).
Ta có: \(f\left( x \right) + \frac{3}{4} = \frac{7}{{16}}x{\left( {x – 3} \right)^2} \Rightarrow u\left( x \right) = f\left( {xf\left( x \right)} \right) + \frac{3}{4} = \frac{7}{{16}}xf\left( x \right){\left( {xf\left( x \right) – 3} \right)^2}\) có 4 lần đổi dấu
Xét \(u'\left( x \right) = \left( {f\left( x \right) + xf'\left( x \right)} \right)f'\left( {xf\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{gathered} f\left( x \right) + xf'\left( x \right) = 0 \Rightarrow 3{n_0}\;\left( 1 \right) \hfill \\ xf\left( x \right) = 1 \Rightarrow 4{n_0}\;\left( 2 \right) \hfill \\ xf\left( x \right) = 3 \Rightarrow 2{n_0}\;\left( 3 \right) \hfill \\ \end{gathered} \right.\) có \(9\) lần đổi dấu.
Thật vậy:\(\left( 1 \right) \Leftrightarrow \frac{7}{{16}}{x^3} – \frac{{21}}{8}{x^2} + \frac{{63}}{{16}}x – \frac{3}{4} + x\left( {\frac{{21}}{{16}}{x^2} – \frac{{21}}{4}x + \frac{{63}}{{16}}} \right) = 0 \Rightarrow 3{n_0}\).\(\left( 2 \right) \Leftrightarrow x\left( {\frac{7}{{16}}{x^3} – \frac{{21}}{8}{x^2} + \frac{{63}}{{16}}x – \frac{3}{4}} \right) – 1 = 0 \Rightarrow 4{n_0}\)Và \(\left( 3 \right) \Leftrightarrow x\left( {\frac{7}{{16}}{x^3} – \frac{{21}}{8}{x^2} + \frac{{63}}{{16}}x – \frac{3}{4}} \right) – 3 = 0 \Rightarrow 2{n_0}\).
Do đó: \(u\left( x \right)\) có 9 điểm cực trị
Vậy hàm số \(g\left( x \right) = \left| {u\left( x \right)} \right|\) có \(9 + 4 = 13\) điểm cực trị.
\(\frac{{\sqrt {129} }}{2}\).
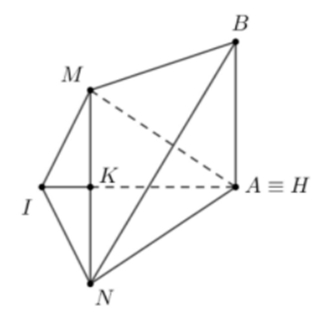 Mặt cầu có tâm \(I\left( { – 2; – 1;2} \right)\), \(R = 3\).Ta có . Đường thẳng \(AB:\frac{{x – 5}}{4} = \frac{y}{{ – 3}} = \frac{{z – 3}}{1}\).Gọi \(H = AB \cap \left( {IMN} \right)\) khi đó \(\left\{ {\begin{array}{*{20}{l}} {IM \bot \left( P \right) \supset AB} \\ {IN \bot \left( Q \right) \supset AB} \end{array} \Rightarrow AB \bot \left( {IMN} \right)} \right.\).Do đó \(H\left( {1;3;2} \right)\) là tọa độ hình chiếu vuông góc của \(I\) trên đường thẳng \(AB\). Dễ thấy \(H \equiv A\) và \(IA \bot MN\) tại trung điểm \(K\) của \(MN\).Áp dụng hệ thức lượng trong tam giác vuông có\(IK.IA = I{M^2} = {R^2} = 9 \Leftrightarrow IK = \frac{9}{{IA}} = \frac{9}{5} \Rightarrow AK = IA – IK = 5 – \frac{9}{5} = \frac{{16}}{5}\).\(MN = 2MK = 2\sqrt {{R^2} – I{K^2}} = 2\sqrt 9 \).Hình chóp \(.AMN\) có cạnh bên \(BA\) vuông góc với đáy nên \({R_{ABMN}} = \sqrt {R_{AMN}^2 + A{B^2}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{\sqrt {104} }}{2}} \right)}^2}} = \frac{{\sqrt {129} }}{2}\).Trong đó \({R_{AMN}} = {R_{IMN}} = \frac{{MN}}{{2\sin \widehat {MIN}}} = \frac{{\frac{{24}}{5}}}{{2\sqrt {1 – {{\left( {\frac{{{3^2} + {3^2} – {{\left( {\frac{{24}}{5}} \right)}^2}}}{{2.3.3}}} \right)}^2}} }} = \frac{5}{2}\) (do tứ giác \(IMAN\)nội tiếp).
Mặt cầu có tâm \(I\left( { – 2; – 1;2} \right)\), \(R = 3\).Ta có . Đường thẳng \(AB:\frac{{x – 5}}{4} = \frac{y}{{ – 3}} = \frac{{z – 3}}{1}\).Gọi \(H = AB \cap \left( {IMN} \right)\) khi đó \(\left\{ {\begin{array}{*{20}{l}} {IM \bot \left( P \right) \supset AB} \\ {IN \bot \left( Q \right) \supset AB} \end{array} \Rightarrow AB \bot \left( {IMN} \right)} \right.\).Do đó \(H\left( {1;3;2} \right)\) là tọa độ hình chiếu vuông góc của \(I\) trên đường thẳng \(AB\). Dễ thấy \(H \equiv A\) và \(IA \bot MN\) tại trung điểm \(K\) của \(MN\).Áp dụng hệ thức lượng trong tam giác vuông có\(IK.IA = I{M^2} = {R^2} = 9 \Leftrightarrow IK = \frac{9}{{IA}} = \frac{9}{5} \Rightarrow AK = IA – IK = 5 – \frac{9}{5} = \frac{{16}}{5}\).\(MN = 2MK = 2\sqrt {{R^2} – I{K^2}} = 2\sqrt 9 \).Hình chóp \(.AMN\) có cạnh bên \(BA\) vuông góc với đáy nên \({R_{ABMN}} = \sqrt {R_{AMN}^2 + A{B^2}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{\sqrt {104} }}{2}} \right)}^2}} = \frac{{\sqrt {129} }}{2}\).Trong đó \({R_{AMN}} = {R_{IMN}} = \frac{{MN}}{{2\sin \widehat {MIN}}} = \frac{{\frac{{24}}{5}}}{{2\sqrt {1 – {{\left( {\frac{{{3^2} + {3^2} – {{\left( {\frac{{24}}{5}} \right)}^2}}}{{2.3.3}}} \right)}^2}} }} = \frac{5}{2}\) (do tứ giác \(IMAN\)nội tiếp).\({\text{2005}}\).
Nếu \(t < 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}} {0 < x < 1} \\ {0 < y < 1} \end{array} \Rightarrow {x^2} + {y^3} < 1 + 1 = 2 \leqslant m} \right.\) (loại). Nếu \(t > 0 \Rightarrow g'\left( t \right) = 0\) có đúng một nghiệm \(t = {t_0} \approx 1,5419\); \(g\left( {{t_0}} \right) \approx 16,9568\).
Suy ra \(m \in \left\{ {17, \ldots ,2023} \right\}\).
Vậy có 2007 số nguyên thỏa mãn
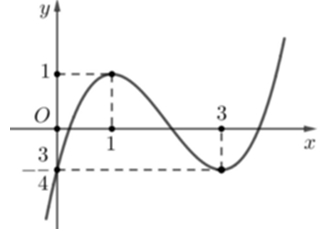 Có bao nhiêu cặp số nguyên dương \(\left( {a;b} \right)\) thỏa mãn \(a + b \leqslant 16\) để phương trình \(f\left( {a{x^2} – 1} \right) = \frac{1}{{bx}}\) có đúng 7 nghiệm thực phân biệt
Có bao nhiêu cặp số nguyên dương \(\left( {a;b} \right)\) thỏa mãn \(a + b \leqslant 16\) để phương trình \(f\left( {a{x^2} – 1} \right) = \frac{1}{{bx}}\) có đúng 7 nghiệm thực phân biệt\(99\).
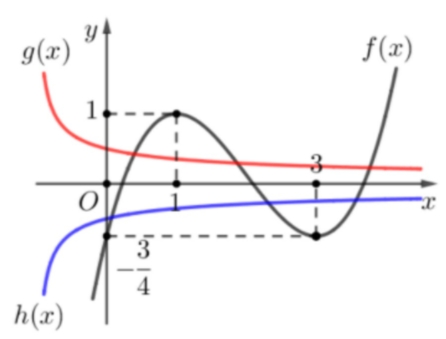 Vậy phương trình có 7 nghiệm khi và chỉ khi \(\left\{ \begin{gathered} g\left( 1 \right) < 1 \hfill \\ h\left( 3 \right) > \frac{3}{4} \hfill \\ \end{gathered} \right.\)\( \Leftrightarrow \left\{ \begin{gathered} \frac{{\sqrt a }}{{\sqrt 2 b}} < 1 \hfill \\ - \frac{{\sqrt a }}{{2b}} > – \frac{3}{4} \hfill \\ \end{gathered} \right.\)\( \Leftrightarrow \sqrt a < \sqrt 2 b\)\( \Leftrightarrow a < 2{b^2}\).+ Nếu \(2{b^2} > 15\)\( \Rightarrow b \in \left\{ {3;…;15} \right\}\)\( \Rightarrow a \in \left\{ {1;…;16 – b} \right\}\)\( \Rightarrow \sum\limits_{b = 3}^{15} {\left( {16 – b} \right)} = 91\) cặp.+) Nếu \(2{b^2} \leqslant 15\)\( \Rightarrow \left[ \begin{gathered} b = 1 \Rightarrow a < 2 \Rightarrow a = 1 \hfill \\ b = 2 \Rightarrow a < 8 \Rightarrow a \in \left\{ {1;...;7} \right\} \hfill \\ \end{gathered} \right.\) có 8 cặp.Vậy tất cả có 99 cặp số nguyên dương thỏa mãn.
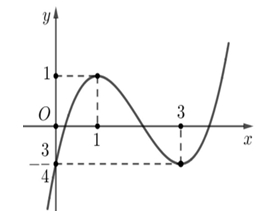
Vậy phương trình có 7 nghiệm khi và chỉ khi \(\left\{ \begin{gathered} g\left( 1 \right) < 1 \hfill \\ h\left( 3 \right) > \frac{3}{4} \hfill \\ \end{gathered} \right.\)\( \Leftrightarrow \left\{ \begin{gathered} \frac{{\sqrt a }}{{\sqrt 2 b}} < 1 \hfill \\ - \frac{{\sqrt a }}{{2b}} > – \frac{3}{4} \hfill \\ \end{gathered} \right.\)\( \Leftrightarrow \sqrt a < \sqrt 2 b\)\( \Leftrightarrow a < 2{b^2}\).+ Nếu \(2{b^2} > 15\)\( \Rightarrow b \in \left\{ {3;…;15} \right\}\)\( \Rightarrow a \in \left\{ {1;…;16 – b} \right\}\)\( \Rightarrow \sum\limits_{b = 3}^{15} {\left( {16 – b} \right)} = 91\) cặp.+) Nếu \(2{b^2} \leqslant 15\)\( \Rightarrow \left[ \begin{gathered} b = 1 \Rightarrow a < 2 \Rightarrow a = 1 \hfill \\ b = 2 \Rightarrow a < 8 \Rightarrow a \in \left\{ {1;...;7} \right\} \hfill \\ \end{gathered} \right.\) có 8 cặp.Vậy tất cả có 99 cặp số nguyên dương thỏa mãn.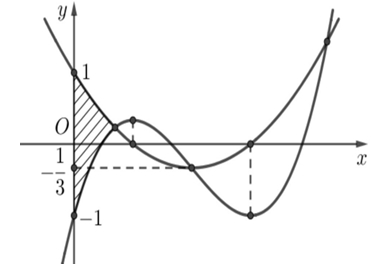 Biết rằng \(f''\left( 2 \right) = 0\) và hai đồ thị hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thỏa mãn \({x_1} + {x_2} + {x_3} = 7\). Diện tích của hình phẳng gạch sọc trong hình vẽ thuộc khoảng nào dưới đây?
Biết rằng \(f''\left( 2 \right) = 0\) và hai đồ thị hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thỏa mãn \({x_1} + {x_2} + {x_3} = 7\). Diện tích của hình phẳng gạch sọc trong hình vẽ thuộc khoảng nào dưới đây?\(\left( {\frac{2}{5};\frac{1}{2}} \right)\).
